Пром-Снег: Промышленность узловых агрегатов

Главная страница сайта Российские промышленные издания (узловые агрегаты)

1 ... 6 7 8 [ 9 ] 10 11 12 ... 27

времени на численное интегрирование. Поэтому точность интегрирования следует ограничивать, руководствуясь соображениями экономии времени.

Тип элемента

Точное решение

Вертикальная нагрузка в точке А

максимальный прогиб в АА

максимальное

напряжение в ВВ

0,26

0,19

0,65

0,53

0,99

1,00

0,55

Момент в А А'

максимальный прогиб в АА

0,22

0,67

0,51

0,99

0,52

1,00

максимальное

напряжение в ВВ

0,22

0,67

0,55

1,00

Фнг. 9.1. Расчет плоского напряженного состояния консоли с помощью различных элементов. Прн увеличении порядка элементов точность возрастает.

9.2. Требуемая точность численного интегрирования

В предыдущей главе указывалось, что матрицы элемента могут быть составлены с использованием численного интегрирования методом Гаусса по я точкам. Объем вычислений при та-

ком интегрировании по плоским областям пропорционален п^ - числу точек, в которых должна быть определена подынтегральная функция, а в трехмерных задачах он пропорционален п?. Поэтому весьма важно установить минимальное достаточное число гауссовых точек.

В настоящей главе рассматриваются задачи теории упругости, требующие вычисления матрицы жесткости элемента. Сформулируем следующее утверждение:

Если при решении задач теории упругости в перемещениях методом конечных элементов точность численного интегрирования достаточна для того, чтобы точно вычислить объем элемента, то процесс сходится [1, 2].

Это утверждение легко доказывается. В пределе при умень-щеиии размеров элемента функции формы дают постоянные значения деформаций и напряжений. Тогда выражения для узловых сил принимают вид

\ {oY[B]dV = {<jf \ [B\dV. (9.1)

Так как

dV = &e.[ndldv,dt, (9.2)

и матрица [В] получена умножением первых производных от Ni иа матрицу [/]-, приходим к выводу, что точное интегрирование соотнощения (9.2) обеспечивает точное вычисление интеграла (9.1). Якобиан выражается через первые производные функции формы [см. выражение (8.18)], поэтому всегда можно определить его порядок, а следовательно, и число гауссовых точек, необходимое для точного интегрирования [3].

Например, для случая двумерного четырехугольного элемента второго порядка детерминант представляет собой квадратичное выражение, для интегрирования которого требуются как минимум две точки. Случаю трехмерной призмы второго порядка соответствует кубичное выражение, для точного интегрирования которого тоже требуется по две точки в каждом направлении.

Этот минимум точек, необходимых для сходимости, не всегда является оптимальным с точки зрения затрат машинного времени. Если для представления области используется небольшое число элементов, интегрирование можно производить с большей точностью, и, наоборот, при использовании большого количества элементов более экономичным может оказаться интегрирование с меньшей точностью.

Ясно, что вычислительные программы должны составляться так, чтобы можно было производить интегрирование с любым количеством точек. Этих точек должно быть не меньше*, чем это

Злемент тртьш порйдт

Злемент четвертого порядно

При использовании дбих юуссовых точек сходимости нет

При исполмовонии трех гауссовых точен Сходимости нет

л = 7

о 3 гауссоОы точки X i гауссовы точки Д 5 gajjccoetix точек

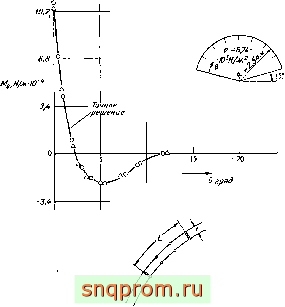
Фиг. 9.2. Влияние порядка численного интегрирования на результаты расчета сферы, нагружеииой внутренним давлением (элементы третьего и четвертого порядков). Сплошной линией показаны точные результаты.

необходимо для сходимости, но и не больше, чем требуется для численного интегрирования.

На фиг. 9.2 в качестве примера иллюстрируется осесиммет-ричная задача о сфере, нагруженной внутренним давлением. При ее решении использовались элементы двух порядков и различное число точек интегрирования. Результаты не требуют комментариев.

Последние работы показывают, что, применяя минимальное число точек интегрирования, в некоторых случаях можно существенно улучшить характеристики элемента. Это объясняется двумя обстоятельствами.

Во-первых, задание формы перемещений всегда увеличивает жесткость (как показано в гл. 2), а снижение точности интегрирования уменьшает ее.

Во-вторых, при малом числе точек интегрирования из рассмотрения исключаются области, в которых для обеспечения непрерывности между элементами на перемещения накладываются чрезмерные ограничения. К этому вопросу мы еще вернемся в гл. 14.

Построение грункцаи формы

9.3. Преимущество применения численного интегрирования в методе конечных элементов [3]

Существенным преимуществом применения в методе конечных элементов численного интегрирования является возможность составления универсальной вычислительной программы. Можно заметить, что для заданного класса задач матрицы всегда одинаково выражаются через функцию формы и ее производные [см., например, (8.14)].

Для вычисления характеристик элемента необходимо, во-первых, задать функцию формы' и ее производные, а во-вторых, установить порядок интегрирования.

Порядок интегрирования

Odaiee соотношение для рассматриваемой матрицы злемента

. Фнг. 9.3. Схема расчета прн численном ии-тегрироваиин по элементам.

Таким образом, вычисление характеристик элемента состоит из трех различных частей, схематически показанных на фиг. 9.3. Чтобы использовать для заданного класса задач различные элементы, необходимо только изменить функции формы, и, наоборот, подпрограммы задания одной функции формы могут применяться в различных классах задач.

Такая схема вычислений позволяет без труда использовать различные элементы для проверки эффективности новых элементов в исследуемой задаче или же применить программу для расчета новых задач без громоздких преобразований (с неизбежными ошибками).

Вычислительная машина при этом используется по назначению, т. е. для проведения расчетов по экономно составленной программе.

Самым большим практическим преимуществом универсальных подпрограмм вычисления функции формы является возможность их проверки с помощью простой программы. Обычно достаточно проверить, правильно ли вычисляются узловые значения и производные. Проверка осуществляется по простым ко-нечно-разностиым формулам после вычисления по подпрограмме значений функций в двух близлежащ-их точках. Иногда используются и другие тесты. Самый интересный из них связан с вычислением собственных значений, но использование его неэкономично [4].

Включение в систему простых точно интегрируемых элементов не должно вызывать опасения, так как время точного и время численного интегрирования при этом почти одинаковы.

9.4. Некоторые практические примеры решения задач [5-10]

двумерных

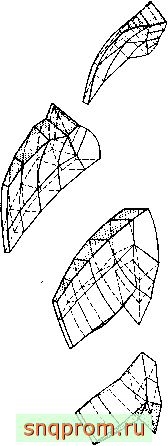
Возможности использования криволинейных элементов для исследования двумерного напряженного состояния иллюстрируются примерами решения осесимметричных задач.

Вращающийся диск (фиг. 9.4). В этом случае для получения решения с достаточной степенью точности необходимо всего восемнадцать элементов. Интересно заметить, что координаты узлов на сторонах элементов третьего порядка задавать не требуется, так как их вычисление предусмотрено программой.

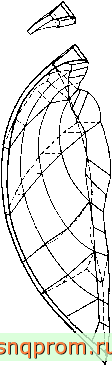
Конический резервуар (фиг. 9.5). Для решения этой задачи используются элементы третьего порядка. Следует отметить, что для описания влияния изгиба как в тонкой, так и в толстой частях резервуара достаточно только одного элемента по толщине стенки. Для получения приемлемого решения при использовании простых треугольных элементов, как мы видели, требовалось несколько слоев элементов.

Полусферический купол (фиг. 9.6). Это еще один пример исследования оболочек, который показывает, как с помощью программы расчета конического резервуара при малом числе элементов можно получить решение задачи для тонкой оболочки. Применяя хорошо известную в теории оболочек гипотезу

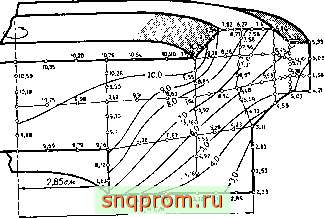
* r 4 4 Расчет вращающегося диска при использовании элементов третьего порядка (18 элементов. 119 узлов, 238 степеней свободы). Шотнрсть 7.85 г/см- £=1.57 Ю' Н/ , v=0.3; 22600 об/ми .

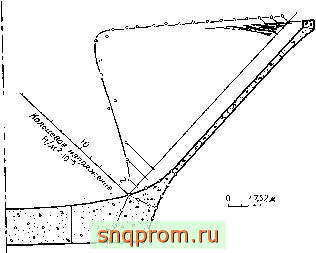
Фиг. 9.5. Конический резервуар,.

L/t изменяется от 9о20

Типичный меменгп

Фиг. 9.6. Тонкая полусферическая оболочка, Решение с использованием 15 и 24 элементов третьего порядка.

О линейности перемещений по толщине, можно уменьшить число степеней свободы и сделать программу более экономичной Методы такого рода подробно рассматриваются в гл. 14.

9.5. Исследование трехмерного напряженного состояния

При решении трехмерных задач, как указывалось в гл. 6, использование сложных элементов позволяет значительно сэкономить время. В этом разделе приведены типичные примеры, в которых используются элементы второго порядка сирендипова типа. Во всех задачах численное интегрирование в каждом направлении производится по трем гауссовым точкам.

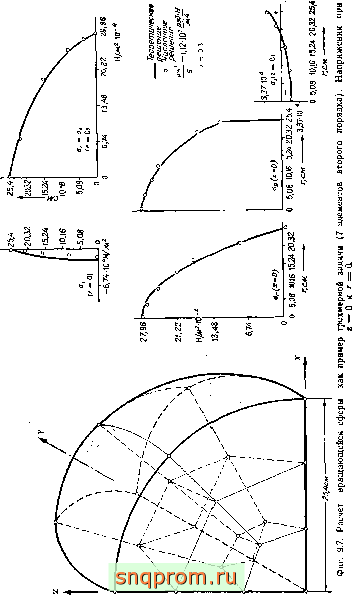
Вращающаяся сфера (фиг. 9.7) [6]. Этот пример, в котором сравниваются рассчитанные и точные значения напряжений, вызванных центробежной силой, позволяет оценить эффективность сильно искривленных элементов. Полученные при исполь-

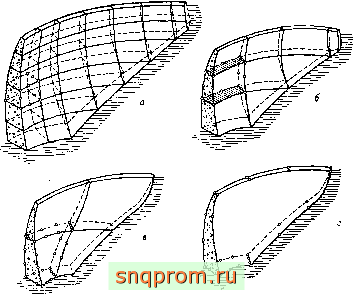
Фиг. 9.8. Арочная плотина на жестком грунте. Различные разбиения на

элементы.

			1}
			Уровень А
	у
	ЧроВень 2


0 го so 40		0 60 ИИ

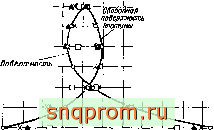
Фиг 9.9, Арочная плотина па жестком грунте. Перемещения центральной

о 32 элемента; Д 9 элементов W, 9 элементов [ВУ. О I элемент (96 степеней свободы).

зовании семи элементов результаты хорошо совпадают с точным решением.

Арочная плотина на жестком грунте. Эта задача, возможно, несколько нереальная с инженерной точки зрения, исследовалась комитетом института гражданского строительства н явилась хорошей проверкой сходимости решения трехмерных задач. На фиг. 9.8 показаны два варианта разбиения плотины на элементы второго порядка и два - на элементы третьего порядка. Фиг. 9.9 иллюстрирует сходимость перемещений в среднем сечении. Видно, что даже в случае одного элемента достигается вполне приемлемая точность.

контанта с водой

-7еА -se.8 -оцг -1S.6 о т ззл 58.е те., sej н/и'-/о^

Сжатие Растяотение

Фнг. 9.10, Арочная плотина иа жестком грунте Напряжения в вертикальном

направлении иа центральной линии. О 32 элемента; А 9 элементов (А); X 9 элементов (В); О I элемент (96 степеней свободы).

Сравнение напряжений (фиг. 9.10) также дает удовлетворительные результаты, хотя при разбиении на крупные элементы заметна значительная осцилляция результатов. Решение, полученное при самом мелком разбиении, можно считать точным , так как оно совпадает с результатами модельного эксперимента и с результатами, полученными другими методами [9].

Приведенные тестовые задачи иллюстрируют универсальность и точность метода. Два ,следуюш.их примера типичны для практических приложений.

Сосуд высокого давления (фиг. 9.11). Арочная плотина и ее основание (фиг. 9.12а). Оба показанных разбиения дают достаточную для практики точность. Первый из этих примеров, в некоторой степени подобный рассмотренному в гл. 6 (фиг. 6.7), демонстрирует возможность значительного уменьшения степеней свободы при использовании сложных элементов.

На фиг. 9,126 изображена в изометрии арочная плотина, разбитая на конечные элементы. Чертеж сделан непосредственно

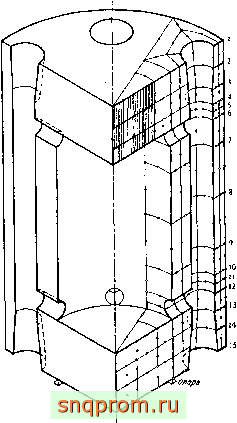
Фиг 9.11. Трехмерная задача о сосуде высокого давления (96 элементов, 707 узлов, 2121 степень свободы).

ПО данным координатного самописца. Такие схемы полезны не только с точки зрения наглядности изображения. Они помогают проверить правильность исходных данных, так как позволяют без труда обнаружить любую грубую ошибку в геометрии. Проверка связанности всех заданных точек также осуществляется автоматически.

Вследствие больших затрат машинного времени при решении сложных трехмерных задач очень важно своевременно исключить ошибки в исходных данных. Поэтому этот н некоторые другие методы проверки [10] должны составлять неотъемлемую часть любой программы.

!20ж

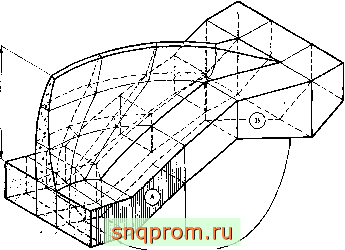
-Нулевые пере- -мещения

Фиг. 9.12а. Расчет арочной плотины с осиоваинем.

9.6. Некоторые общие замечания об элементах высокого порядка

Чем выше порядок элемента, тем труднее становится физическая интерпретация. Это не столь уж существенно, если в результате, получается лучшая аппроксимация, однако в практических приложениях могут возникать дополнительные трудности. Например, при использовании элементов высокого порядка было бы неправильно локализовать распределенные нагрузки, основываясь на интуиции.

В гл. 4 было показано, что в треугольном элементе нагрузка, вызванная силой тяжести, локализуется в виде трех равных узловых усилий (подразд. 4.2.7). Этот результат совпадает с тем, что мы называем очевидным. Соответствующая локализация для двумерных элементов сирендипова типа (фиг. 7.4, гл.7) приводит к распределению нагрузки по узлам, показанному иа фиг, 9,13. Только для первого, простейшего из этого семейства

S m т

элемента результат соответствует здравому смыслу. Во всех остальных случаях в угловых точках получается отрицательная нагрузка - факт совсем не очевидный.

I i i

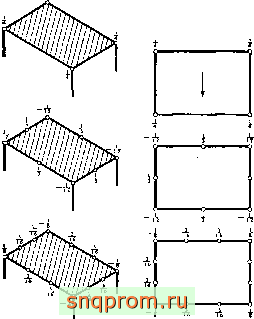
Фиг. 9.13. Распределение равномерной массовой силы по узлам. Семейство прямоугольных э.темеитов. Показаны доли общего веса.

Фиг. 9.14. Распределение по узлам равномерной поверхностной нагрузки, действующей на границе двумерных и трехмерных элементов.

Если элементы к тому же искривлены, то нагрузка распределяется еще более сложны.м образом н в этом случае нужна особая осторожность.

Здесь инженер может сказать, что с физической точки зрения в пределе результат должен быть таким же, как и при распределении нагрузхи по узлам поровну. Конечно, это должно быть именно так, но при разбиении на конечные элементы такое противоестественное, но согласующееся с теорией распределение нагрузки гарантирует большую точность.

Как следует из фиг. 9.14, распределение повер.хностной нагрузки также нельзя предсказать.

Следует иметь в виду, что все эти рассуждения относятся и к представлениям сил между элементами обычными инженерными способами.

И наоборот, в областях, близких к месту приложения сосредоточенных нагрузок, распределение напряжений описывается неверно, и в окрестности таких нагрузок иногда можно получить несколько неожиданные значения напряжений. Это вовсе не

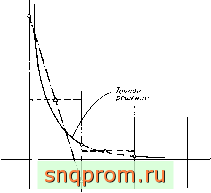
Фиг. 9.15. Аномалии, которые могут появляться в окрестности точки приложения сосредоточенной нагрузки при использовании сложных элементов.

---элемент с постоянной деформацией;-----элемент с линейно изменяющейся

деформацией.

говорит об уменьшении точности, а указывает на то, что усреднение по элементу позволяет лучше представить действительную картину напряжений.

На фиг. 9.15 проводится качественное сравнение напряжений вблизи такой особой точки, определенных при постоянных деформациях и линейном законе изменения деформаций в элементах. Попытка улучшить аппроксимацию напряжений с помощью использования более сложных элементов иногда дает возможность получить более точное значение напряжения в особой точке. Однако при этом вблизи такой точки может произойти противоестественная смена знака напряжения, чего не бывает при использовании простых элементов. Ясно, что в таких случаях следует применить сглаживание и внимательно подойти К оценке результатов

ЛИТЕРАТУРА

1. Irons в. М., Engineering Application ol Numerical Integration in Stiffness Mettiod, JAIAA, 4, 2035-2037 (1966); есть русский перевод: Айронс, Инженерные приложения численного интегрирования в методе жесткостей. Ракетная техника и космонавтика, 4, № И, стр. 213-216 (1966).

2. Irons В. М., Comment on StifIness Matrices lor Sector Element> by Ra-ju I. R., Rao A. K., JAJAA, 7, 156-157 (1969); есть русский перевод: Айронс, Замечание к статье Матрицы жесткости элементов в форме сектора . Ракетная техника и космонавтика, 8, № 3, стр. 271 (1970).

3. Irons В. М., Discussion, р. 328-331, of Finite Element Techniques in Structural Mechanics, Tottenham H., Brebbia C, eds., Southampton Univ. Press, 1970.

4. irons B. M., Testing and Assessing Finite Elements by an Eigenvalue Technique, Proc. Conf. on Recent Developments in Stress Analysis, / Br. Soc. St. An., Royal Aero Soc. (1968).

5. Zienkiewicz O. C, Irons B. M., Ergatoudis J., Ahmad S., Scott F. C, Isoparametric and Associated Element Families for Two and Three Dimensional Analysis, Proc. Course on Finite Element Methods in Stress Analysis, Holand I., Bell K., eds., Trondheim Tech. Univ., 1969.

6. Irons B. M., Zienkiewicz O. C, The Isoparametric Finite Element System - a New Concept in Finite Element Analysis, Proc. Conf. Recent Advances in Stress Analysis, Royal Aero Soc, 1968.

7. Ergatoudis J. G., Irons B. M Zienkiewicz 0. C, Curved, Isoparametric, Quadrilaterab Elements for Finite Element Analysis, Int. J, Solids and Struct 4, 31-42, (1968),

8. Ergatoudis J, G., Isoparametric Elements in Two and Three Dimensional Analysis, Ph. D. Thesis, Univ, of Wales, Swansea, 1968.

9. Ergatoudis J. G., irons B. M., Zienkiewicz O. C, Three Dimensional Analysis of Arch Dams and Their Foundations, Symp. on Arch Dams, Inst Civ Eng., London, 1968.

10. Zienkiewicz O. C, Irons B. M., Campbell J., Scott P., Three Dimensional Stress Analysis, Int. Un. Th. Appl. Mech. Symp. on High Speed Computine in Elasticity, Liege, 1970.

10.1. Введение

Во всех задачах предыдущих глав основные зависимости между напряжениями и деформациями приведены в точной форме, хотя окончательное решение находилось приближенно. В классической теории пластин [1], чтобы упростить задачу и свести ее к двумерной, с самого начала вводятся некоторые гипотезы, а именно делаются предположения о линейном изменении деформаций и напряжений по нормали к плоскости пластины. Так называемые точные решения теории пластин справедливы только тогда, когда справедливы эти допущения, т. е. если пластины тонкие и прогибы малы.

При решении представленных здесь задач использовались допущения классической теории пластин, и, следовательно, точность приближенных решений должна проверяться на известных задачах теории пластин. Пределы их применимости будут такими же, как и теории пластин.

Деформированное состояние пластины полностью описывается одной величиной - прогибом w срединной поверхности пластины. Однако теперь условие непрерывности между элементами должно быть наложено не только на эту величину, но и на ее производные. Это необходимо для того, чтобы пластина оставалась сплошной и не появлялись изломыПоэтому в каждой узловой точке обычно приходится удовлетворять условиям равновесия и непрерывности.

Выбрать подходящую функцию формы теперь гораздо сложнее. В самом деле, если на границе между элементами требуется выполнение условия непрерывности' угла наклона, то непропорционально возрастают математические и вычислительные трудности. Однако относительно просто получить функции формы, которые, сохраняя непрерывность w между элементами, допускают нарушение непрерывности угла наклона, хотя, конечно, не в узловых точках, где условия непрерывности заданы. Если такие функции удовлетворяют критерию постоянства деформаций , то решение может сходиться (см. гл. 2). В первой части этой главы рассматриваются именно такие несогласован-

) Если появляется излом, то вторая производная (кривизна) становится бесконечной и в выражении для энергии появляются бесконечные члены.

ные функции формы. Во второй части вводятся новые функции, которые позволяют удовлетворить условиям непрерывности. С помощью этих согласованных функций можно получить более корректное, но, как правило, менее точное решение. Для практического применения рекомендуются функции, описанные в первой части этой главы.

Элементом простейшей формы является прямоугольник. Использование треугольных н четырехугольных элементов связано с некоторыми трудностями, и они будут рассмотрены позднее; для расчета пластин произвольной формы и оболочек именно такие элементы являются основными.

10.2. Формулировка задачи об изгибе пластин в перемещениях

В соответствии с обычной теорией тонких пластин перемещение пластины однозначно определяется известным во всех точках прогибом w.

Запишем его в общем виде:

w = [N][bY, (10.1)

где функции формы зависят от декартовых координат х, у, а столбец {6} содержит все (узловые) параметры элемента.

Обобщенные деформации и напряжения должны быть теперь определены так, чтобы их скалярное произведение, как и в гл. 2, давало внутреннюю работу. Таким образом, определим деформации (фиг. 10.1) как

{е} =

ду , d-w дхду

(10.2)

Соответствующими напряжениями являются обычные изгибающие и крутящие моменты на единицу длины в направлениях X к у:

(10.3)

Так как истинные деформации и напряжения изменяются линейно по толщине пластины [1], то их можно найти из соотношений

о^ = -г и т. д.,

ИЗГИБ ПЛАСТИН

У

Плоскость

х-у

Фиг. 10.1. Результирующие напряжений или просто напряжеиия при изгибе

пластин.

где г отсчитывается от срединной плоскости пластины, at - толщина пластины.

Можно показать, что произведение выражений (10.2) и (10.3) соответствует внутренней работе.

Так как теперь в выражение для деформаций входят вторые производные, то, согласно критерию непрерывности, функции формы должны обеспечивать непрерывность как а), так и угла-наклона нормали к границе между элементами.

Критерий постоянства деформации требует, чтобы внутри элемента можно было воспроизвести любое постоянное значение второй производной.

Чтобы по крайней мере приближенно удовлетворить условию непрерывности угла наклона, в качестве узловых параметров рассматриваются три компоненты перемещений: во-первых, пе-

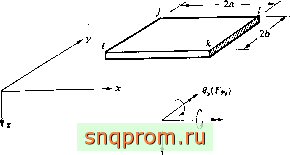
Силы и соответствующие перемещения

Фиг. 10.2. Прямоугольный элемент пластины.

ремещение Wn в направлении г, во-вторых, угол поворота (еу) вокруг оси у и, в-третьих, угол поворота (ех)п вокруг оси х. На фиг. 10.2 показаны положительные направления поворотов, определяемые по правилу правой руки. Их величины задаются векторами, направленными по соответствующим осям.

Ясно, что углы наклона w и углы поворота совпадают с точ-ностьвэ до знака, поэтому можно записать

(10.4)


			\ду Ji
	л
	9j,;

Как показано на фиг. 10.2, узловыми силами, соответствующими этим перемещениям, являются сила и два момента:

{Fi} = \FM\- (10.5)

F, ,)

Если известна матрица [В], то -матрица жесткости и все остальные матрицы строятся обычным образом с помощью со-отнощеннй гл. 2.

Из определений (10.1) и (10.2) следует, что

[В(] =

(10.6)

Запись функций формы в квадратных скобках подчеркивает, что онн являются матричными величинами, состоящими из трех элементов.

Матрица упругости [D] входит в обычное соотнощение:

{a}{Af} = [D]({e}-{8o})-f {оо}. (10.7)

Для изотропной пластины имеем (см. [1])

1 V О

[D] =

12(1 -v2

1 -у

(10.8)

Чтобы описать поведение ортотропной плиты, главные направления упругости которой совпадают с осями хну.

1 ... 6 7 8 [ 9 ] 10 11 12 ... 27