Главная страница сайта
Российские промышленные издания (узловые агрегаты)
1 ...
5 6 7 [
8 ]
9 10 11 ...
27 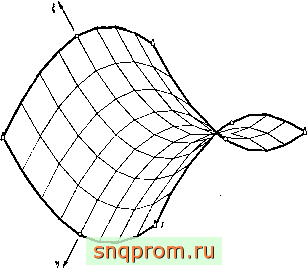
-- х- >
X X ж
х-- >
X X. X
>
/ -V ✓
✓ -X

Фнг. 8.5. (продолжение).
Фнг; 8.5. Преобразование плоских (или параболических) элементов в трехмерном пространстве.
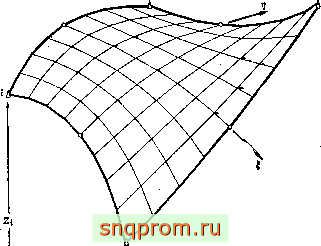
Фиг. 8.6. Требование совместности прн разбиении области.
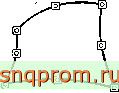
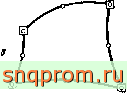
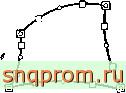
Фиг. 8.7. Различные типы элементов.
о точка, в которой заданы координаты; □ точки, в которых заданы параметры функции, а -изопараметрический элемент; б-суперпараметрнческий элемент; з -субпараметрический элемеит.
Однако для определения ф можно было бы использовать только четыре угловые точки (фиг. 8.7,6). Такие элементы называются суперпараметрическими, так как для них изменение геометрии описывается более полно, чем изменение неизвестных.
Аналогично если для определения ф вводится больше узлов, чем для задания геометрии, то элементы называются субпараметрическими (фиг, 8.7, S). Такие элементы на практике используются чаще, чем суперпараметрические.
8.5. Удовлетворение критерию постоянства производной
Выбор удовлетворяющих условию непрерывности функций, которые определяют геометрию элемента и закон изменения ф, достаточно широк, причем эти функции не обязательно должны быть одинаковыми. Однако критерий постоянства деформаций (гл. 2), или критерий постоянства производной (гл. 3), накладывает некоторое ограничение.
Напомним, что для сходимости необходимо, чтобы в каждой точке элемента путем подбора соответствующих узловых значений ф можно было получить любое произвольное постоянное значение первых производных (это справедливо для функционалов, содержащих только производные первого порядка). При этом соотношение
ф = [М]{фГ=1ф,=а^--а2К-\-щу-{-а,г, где (8.5) [N] = [N{1, л, 1)1 должно быть справедливо для любых постоянных ai-i и соответствующих значений {фу. В самом деле, в узловых точках должно выполняться равенство
= а, + OiXi -f ЩУ1 + ctiZi,
(8.6)
(8.8)
так что первое соотношение можно переписать в виде
т {ФГ = а, Z , + 2 £ NiXi -f ct, Z Ny -f 04 S NiZi -
= Oi-f ctsAf-f oji/042. (8.7)
Оно всегда будет удовлетворяться, если
£ NiXi = x, ZNiy,=y, Т, NiZi=z.
Из формул преобразования координат [соотношение (8.2)] следует, что
T,N,x,=x,
Y.NiZi = z, (8.9)
и, следовательно, справедлива следующая теорема:
Теорема 3. Все изопараметрические элементы! для которых JNiil), удовлетворяют условию постоянства производной.
Можно показать, что это условие является необходимым и что теорема справедлива для субпараметрического преобразования в случае, если [N] можно представить в виде линейной комбинации [Л^], т. е. если
Ni = Y,Ci,N,. . (8.10)
ПРЕОБРАЗОВАНИЯ
8.6. Вычисление матриц элемента (преобразование координат I. Л- ?)
Для применения метода конечных элементов должны быть найдены матрицы, определяющие свойства элемента, такие, как жесткость н др. Эти матрицы будут иметь внд
(8.11)
\[G]dV,
где [G] зависит от функций или их производных по глобальным координатам. В качестве примера рассмотрим матрицу жесткости
\[Bf[DmdV (8.12)
и соответствующие векторы нагрузки \m{p}dV.
(8.13)
Для некоторого класса задач теории упругости матрицы [В] были выписаны в явном виде [см. равенства (4.10), (5.6) и (6.11)]. Первое из них, равенство (4.10), относящееся к плоским задачам, дает
- dNi
дх О dNi
О
ду dNj
(8.14)
) Прн определении напряжений это условие .просто означает, что перемещение тела как жесткого це.того не должно вызывать никаки.ч деформаций-требование менее ограничительное, чем условие постоянства производных.
Здесь штрих, использованный в гл. 4 для обозначения функций формы, опущен, ибо теперь эти функции являются скалярными и относятся ко всем компонентам перемещения. Заметим, что такая форма записи носит достаточно общий характер и справедлива для всех двумерных элементов, используемых при решении плоских задач теории упругости, независимо от числа узлов (или неузловых параметров) в элементе. Это замечание относится ко всем рассматриваемым в книге задачам.
Для вычисления матриц необходимо сделать два преобразования. Во-первых, поскольку Nt заданы в локальных (криволинейных) координатах, необходимо каким-либо образом выразить глобальные производные, входящие в (8.14), через локальные производные.
Во-вторых, элементарный объем (или поверхность), по которому должно проводиться интегрирование, нужно представить в локальных координатах и соответствующим образом изменить пределы интегрирования.
Рассмотрим, например, систему локальных координат I, ц, t, и соответствующую систему глобальных координат х, у, z. Используя правило частного дифференцирования, можно записать, например, производную по в виде
злг,
дЩ дх дЛГ, ду . dNi дг д| ду д| дг dl
(8.15)
Дифференцируя аналогично по остальным двум координатам и используя матричную форму записи, получаем
| | | | | | | | IdNi ] | |
| | | | | | | | | |
dN[ дц | | дх di, | dy dr\ | dz dn | | dNi dff | | dNi dy | . (8.16) |
| | | | | | | | | |
| | dZ | | dl | | dz J | | I dz | |
Левая часть этого выражения легко вычисляется, так как функции Ni заданы в локальных координатах. Кроме того, поскольку координаты X, у, z связаны с криволинейными координатами [соотношение (8.2)], матрица [У] выражается через локальные координаты. Эта матрица называется матрицей Якоби.
Чтобы найти глобальные производные, обратим матрицу [/] и запишем
dy dNi
dl dN[ дц
(8.17)
Выражая [/] через функции формы [N ], определяющие преобразование координат (которые, как мы видели, только для изопараметрических элементов совпадают с функциями формы Щ), получаем
| | | | | dNi dl | | | dN di |
[/]= | | | | dNi дц | | | |
| | | | | | | | dNi dZ |
dN, dN,
Xi У2 22
(8.18)
Для преобразования переменных и области интегрирования применим стандартный прием, использующий определитель матрицы [/]. Так, например, элементарный объем преобразуется следующим образом:
dx dydz-=det []didцdZ.
(8.19)
Преобразование такого типа справедливо при любом числе координат. Доказательство читатель может найти в обычных учебниках по математике. Особенно хорошо изложен этот вопрос в книге Муриагана [6]) (см. также приложение 5).
Если предположить, что матрица [/] имеет обратную, то определение характеристик элемента сводится к вычислению интегралов типа (8.11).
Если криволинейные координаты являются нормализованными координатами, соответствующими прямой правильной призме, то интеграл (8.11) можно записать в виде
1 I J
\ \ J [Gil, n, Q]didr]di.
(8.20)
) Определитель матрицы Якоби в литературе называется якобианом и часто записывается в внде
Интегрирование производится по объему именно такой, а не искривленной призмы, поэтому пределы интегрирования записываются просто. Для одномерных и двумерных задач получаются интегралы соответственно по одной и двум переменным с простыми пределами интегрирования.
Хотя пределы интегрирования простые, выражение для [G] в явном виде, к сожалению, очень сложное. Поэтому, за исключением некоторых простейших элементов, точно интегрирование провести не удается и приходится прибегать й численному интегрированию. Впрочем, это, как мы увидим далее, не так уж плохо и имеет то преимущество, что позволяет избежать алгебраических ошибок и составить типовые программы для различных, классов задач независимо от вида элемента. При использовании численных методов обращение матрицы [/] никогда не производится явно.
8.7. Матрицы элемента. L-коордннаты
Соотношения (8.2) преобразования координат и асе последующие теоремы в равной степени справедливы для любой системы локальных координат. В частности, с их помощью координаты Li, Ц, ..., введенные в предыдущей главе для треугольников и тетраэдров, можно связать с глобальными декартовыми координатами.
Большая часть рассуждений предыдущей главы остается в силе, если соответствующим образом переименовать локальные координаты. Однако появляются два существенных отличия.
Jo-первых, локальные координаты не являются независимыми и число их на единицу больше, чем декартовых. Матрица [J], следовательно, становится прямоугольной и не допускает обращения. Во-вторых, меняются пределы интегрирования, которые теперь должны соответствовать треугольным или тетраэдральным первичным элементам.
Простейший, хотя, возможно, и не самый изящный, способ избавиться от первого затруднения - это считать последнюю переменную зависимой. Так, например, для тетраэдра (используя обозначения предыдущей главы) введем формально
Г] = 12,
(8.21)
Таким образом, равенство (8.16) и все соотношения вплоть до (8.19) сохраняются без изменений.
Поскольку функции Ni выражаются через координаты Ц, L2 и т. д., то
dl - дЦ dl дЦ 01 дЦ dl f dU dl °-> Учитывая (8.21), приходим к равенству dNj dNt dN[ d ~ dL, dL,
Остальные производные получаются аналогично.
Пределы интегрирования в (8.20) заменяются на пределы, соответствующие тетраэдру, т. е.
I п 1-11-5
\ \ \ IGih п, 4)lrf?rfr,rf£. (8.23)
ко о
Аналогичная процедура справедлива и для треугольника.
Заметим, что сложность выражения для [G] опять вызывает необходимость численного интегрирования, которое должно производиться по простой, неискрив-ленной, первичной области, т. е, по треугольнику Или тетраэдру.
Отметим, наконец, что каждый из элементов, рассмотренных в предыдущей главе, может быть деформирован в криволинейный. Иногда, как, например, для треугольной призмы, одновременно используются и прямоугольные и L-координаты (фиг. 8.8). Сделанные ранее замечания относительно зависимости координат остаются в силе.

Фиг. 8.8. Криволинейная трехгран мая призма.
ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
8.S. Одна переменная
Еще в гл. 5, где рассматривалась относительно простая задача об осесимметричном напряженном состоянии и использовались простые треугольные элементы, отмечалось, что точное интегрирование выражений, входящих в матрицы элемента, связано с большими трудностями. В таких задачах, как и при использовании сложных криволинейных элементов, возникает необходимость численного интегрирования.
Здесь мы изложим основные принципы численного интегрирования и приведем таблицы квадратурных коэффициентов.
Интеграл от функции одной переменной можно вычислить двумя основными методами [7, 8].
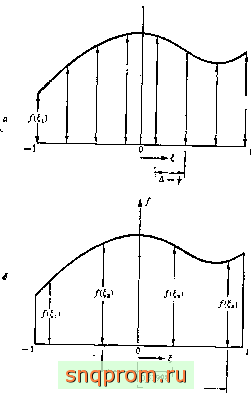
Квадратура Ньютона - Котеса). Сначала априори выбираются точки, обычно равноотстоящие друг от друга, в которых вычисляются значения функций. Затем строится полином,
0,86! 13
Фиг. 8.9. Интегрирование методами Ньютона - Котеса (а) и Гаусса (б) Ойя метода позволяют точно проинтегрировать полином седьмой степени (те погрешность имеет порядок О (А')). i . и
рование^ Р УР попользуется в.место термина численное иитегри-
значения которого совпадают со значениями функции в этих точках, и точно интегрируется (фиг. 8.9).
Так как п значений функции определяют полином степени п- 1, ошибка имеет порядок 0(Д) , где Д - расстояние между точками. В результате получаем известные квадратурные формулы Ньютона - Котеса, в соответствии с которыми интеграл можно записать в виде
~ (8.24)
при интегрировании в пределах от -1 до -fl (фиг. 8.9, а). Например, если п = 2, то
/ = f(-l) + f(l)- (8.25)
При /1 = 3 получается известная формула трапеций
/ = [f(-l) + 4f(0)-f f(l)], (8.26)
при /1 = 4 - формула одной трети Симпсона
/ = [/(-l) + 3f(-)-f 3f(l)-ff (1)]. (8.27)
Формулы интегрирования для различных п (до /г = 20 включительно) приведены у Копаля [8].
Квадратура Гаусса. Если значения функции вычисляются не в априорно заданных точках, а так, чтобы достигалась наилучшая возможная для данного количества точек точность, интегрирование выполняется точнее. Если положить, что
1= \ f(s)rf = EHy.
(8.28)
и снова представить подынтегральную функцию в виде полинома, то нетрудно увидеть, что для п точек интегрирования получим 2п неизвестных (/, и г), и, следовательно, можно построить и точно проинтегрировать полино.м степени 2п - 1 (фиг. 8.9,6). В результате ошибка будет иметь порядок 0(Д)2п.
Решить полученную систему уравнений трудно, но с помощью некоторых математических приемов [7] решение можно получить в полиномах Лежандра. Поэтому этот метод часто называется квадратурой Гаусса - Лежандра.
В табл. 8.1 приведены координаты точек и весовые коэффициенты для интегрирования по Гауссу.
Таблица 8.1
Абсциссы в весовые коэффициенты квадратурной формулы Гаусса
1 л
f{x)dx= 2 Hjf(aj)
±а
Я
1 = 2
0,57735 | 02 691 | 89 626 | О | 1,00000 | 00 000 | 00 000 |
0,77459 | 66692 | 41 483 | п = о | 0,55555 | 55 555 | 55 556 |
0,00000 | 00 000 | 00 000 | а | 0,88888 | 88 888 | 88 889 |
0,86113 | 63115 | 94 053 | | 0,34785 | 48 451 | 37 454 |
0,33998 | 10 435 | 84 856 | | 0,65214 | 51 548 | 62 546 |
| | | п = 5 | | | |
0,90617 | 98 459 | 38 664 | | 0,23692 | 68 850 | 56 189 |
0,53846 | 93101 | 05 683 | | 0,47862 | 86 704 | 99 366 |
0,00000 | 00 ООО | 00 000 | | 0,56888 | 88 888 | 88 889 |
| | | | п = 6 | | | |
0,93246 | 95 142 | 03 152 | | 0,17132 | 44 923 | 79 170 |
0,66120 | 93 864 | 66265 | | 0,36076 | 15 730 | 48 139 |
0,23861 | 91 860 | 83197 | | 0,46791 | 39 345 | 72 691 |
| | | | п = 7 | | | |
0,94910 | 79 123 | 42 759 | | 0,12948 | 49 661 | 68870 |
0,74153 | II 855 | 99 394 | | 0,27970 | 53914 | 89 277 |
0,40584 | 51 513 | 77 397 | | 0,38183 | 00 505 | 05 119 |
0,00000 | 00 ООО | 00 ООО | п = 8 | 0,41795 | 91 836 | 73 469 |
0,96028 | 98 564 | 97 536 | 0.10122 | 85 362 | 90 376 |
0,79666 | 64 774 | 13 627 | | 0,22238 | 10 344 | 53 374 |
0,52553 | 24 099 | 16 329 | | 0,31370 | 66 458 | 77 887 |
0,18343 | 46 424 | 95 650 | | 0,36268 | 37 833 | 78 362 |
| | | | = 9 | | | |
0,96816 | 02 395 | 07 626 | | 0,08127 | 43 883 | 61 574 |
0,83603 | И 073 | 26 636 | | 0,18064 | 8! 606 | 94 857 |
0,61337 | 14 327 | 00 590 | | 0,26061 | 06 964 | 02 935 |
0,32425 | 34234 | 03 809 | | 0,31234 | 70 770 | 40 003 |
0,00000 | 00 000 | 00 000 | | 0,33023 | 93 550 | 01 260 |
| | | | п= 10 | | | |
0,97390 | 65 285 | 17 172 | | 0,06667 | 13 443 | 08 688 |
0,86506 | 33 666 | 88 985 | | 0,14945 | 13 491 | 50 581 |
0,67940 | 95 682 | 99 024 | | 0,21908 | М 625 | 15 982 |
0,43339 | 53 941 | 29247 | | 0,26926 | 67 193 | 09 996 |
0,14887 | 43 389 | 81 631 | | 0,29552 | 42 247 | 14753 |
6 Зак. 613 |
В методе конечных элементов сложность вычислений заключается в определении значений интегрируемой функции f, поэтому в дальнейшем будет применяться только формула Гаусса, использующая минимальное число значений функции.
Можно получить формулы для интегрирования с заданной степенью точности выражений вида
(8.29)
при известной функции w{l), если опять заменить f() полиномом [7].
8.9. Прямоугольник или прямая призма
Проще всего взять интеграл
/=5 5 f{l,r))dldri.
(8.30)
вычисляя сначала значение внутреннего интеграла в предположении, что Т1 - постоянная, т. е. используя формулу
5 f (I, Ti) d = Hjf {l r\)= (Ti). (8.31)
-I /=1
Вычисляя затем внешний интеграл, получаем
I п п п
7 = 5 Ф (Т1) dTi = Ягф (Т1,) = X Я, Я^f (, ,1,) =
1=1 1=
1-1 i-i
Аналогично для прямой призмы имеем i I I
/= S 5 S fil, г\, l)dldr]d-. -1 -1 -I
п п п
(8.32)
(8.33)
Здесь предполагалось, что число точек иитегрировання в каждом направлении одинаково.
Интересно отметить, что двойное суммирование легко заменить простым по (п X п) точкам для прямоугольника (или по п? точкам для куба). На фиг. 8.10 показано девять точек, необходимых для точного интегрирования полинома пятого порядка по каждой из переменных.
Однако к решению этой задачи можно было бы подойти с другой стороны и интегрировать точно полином пятого порядка по двум переменным. В этом случае в каждой точке пришлось бы определить две координаты и значение подынтегральной функции f, входящей в весовую формулу типа
I I т
/=5 5 f(g, Ti)drfTi = 2eD,f( 7i,).
(8.34)
Фиг. 8.10. Точки интегрирования для л-= 3 в квадратной области. (Точно интегрируется по-.тином пятой степени по каждой переменной.)
Оказывается, что при этом для достижения той же точности достаточно было бы использовать только семь точек. Формула такого типа для трехмерного кирпичика получена и с успехом использована Айронсом [9].
8.10. Треугольник или тетраэдр
Для треугольника интегралы по L-координатам имеют вид
/ = 5 5 /(L Ц, L,)dL,dL,.
(8.35)
m=I /-I (=-1
Оиять можно было бы использовать п гауссовых точек и получить сумму типа, рассмотренного в предыдущем разделе. Однако теперь пределы интегрирования сами содержат переменные, поэтому для второго интегрирования удобно использовать выражения вида (8.29) квадратуры Гаусса, где w - лнией-ная функция. Это было сделано Радо [10, 11]. В табл. 8.2 приведены весовые коэффициенты, входящие в выражение
I=tiwf{Li, L Ц),
Таблица 8.2
Коэффициенты для интегрирования по формулам Гаусса и Радо
Количество точек интегрирования в кажлом направлении | А/т J = h п | | AI \1] /=1, п | .4SI71 1 = 1, п |
п = 1 | | | 0,3333333333 | 0,75 |
| | | | (1.0) | (0,25) |
П = 2 | 0,2113248654 | | 0,1550510257 | 0,3764030627 |
| | 0,7886751346 | | 0,6449489743 | 0,5124858262 |
| | | | (1,0) | (0,1111111111) |
п = 3 | 0,1(27016654 | 0,2777777778 | 9,0885879595 | 0,2204622112 |
| | | 0,4444444444 | 0,4094668644 | 0,3881934688 |
| | 0,8872983346 | 0,2777777778 | 0,7876594618 | 0,3288443200 |
| | | | (1,0) | (0,0.625) |
И = 4 | 0,0694318442 | 0,1739274226 | 0,0571041961 | 0,1437135608 |
| | 0,3300094782 | 0,3260725774 | 0,2768430136 | 0,2813560151 |
| | 0,6699905218 | 0,3260725774 | 0,5835904324 | 0,3118265230 |
| | 0.9305681558 | 0,1739274226 | 0,8602401357 | 0,223103901! |
| | | | (1,0) | (0,04) |
и = 5 | 0,0469100770 | 0,1184634425 | 0,0398098571 | 0,1007941926 |
| | 0,2307653449 | 0,2393143353 | 0,1980134179 | 0,2084506672 |
| | | 0,2844444444 | 0,4379748102 | 0,2604633916 |
| | 0,7692346551 | 0,2393143353 | 0,6954642734 | 0,2426935942 |
| | 0,9530899230 | 0,1184634425 | 0,9014649142 | 0,1598203766 |
| | | | (1,0) | (0,277777778) |
где
L2 = AJ{j){\-L,),
W = AS(i)H(f)(\~L,).
(8,36)
Аналогичные соотношения можно получить и для тетраэдра.
На фиг. 8.11 показано расположение точек интегрирования в треугольниках при п = 1, 2, 3. Видно, что они расположены неравномерно и несимметрично. Кроме того, в направлениях и, 1г, Ьз точность интегрирования различна. Другое (более изящное) расположение точек, предложенное Хаммером и др. [12], позволяет существенно упростить расчет; весовые коэффи-
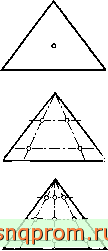
Фиг. 8.11. Точки интегрирования для треугольника при использовании метода Гаусса - Радо.
циенты для выражений, аналогичных (8.34), приведены в табл. 8.3 [13].
Можно убедиться, что точек всегда столько или немного больше, чем требуется для получения полных полиномов заданного порядка.
Очевидно, что эти результаты можно обобщить и на тетраэдры. В табл. 8.4 представлены некоторые формулы из работы [12].
8.11. Заключительные замечания
В этой главе показано, каким образом можно построить большое количество криволинейных элементов. Необходимость использования методов численного интегрирования потребовала описания некоторых из них. Дальнейшие подробности можно найти в различных учебниках по численному анализу.
Очевидно, что численное интегрирование является приближенным. Вопрос о том, какая степень точности необходима в практических задачах, будет рассмотрен в следующей главе. Там же будут приведены основные принципы организации программ при использовании численного интегрирования.
Таблица 8.3
Формулы численного интегрирования для треугольников
Порядок элемента
Рисунок
Z.-координаты
Весовые коэффициенты
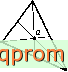
R = om
111 3 3 3
Второй.

R = 0{h)

Д = 0(Л')
27 48
25 48
Эта формула не рекомендуется нз-за отрицательного весового коэффициента и ошибок округления

I I 1
21 60
3 60
Продолжение табл. 83
Порядок элемента | Рисунок | | Точки | L-координаты | Весовые коэффициенты |
Пятый | | R=o т | а Ь с d е 1 g | 1 1 1 3 3 3 ai> Pi. Pi Pi. 1. Pi Pi. P.. o. 2. Pa. Ps P2. 2, P2 P2. Pa. 2 | 0,225 0,13239415 0,12593918 |
| | | | а, = 0,05971587 р, = 0,47014206 а, = 0,79742699 р2 = 0,10128651 | |
Таблица 8.4
Формулы численного интегрирования для тетраэдра
Порядок элемента | Рисунок | | Точки | Пространственные L-координаты | Весовые коэффициенты |
| | | R = 0\h) | а | 1111 4 4 4 4 | |
| | | | | а | а, Р, Р. Р | |
| | | R = 0 (h) | | Р, а, р, Р Р. Р. а, р р. Р, Р, а а = 0,58541020 Р = 0,13819660 | |
Продолжение табл. 8.4
Порядок элемента | Рисунок | | Точки | Пространственные L-ксординаты | Весовые коэффициенты |
| | | | | а | | 4 | | | |
| | | | | Ь | ¥ | | | | 9 20 |
| | | = 0(А<) | с | | | | | |
| | | ±л | | | | | | |
| | | | | | | | | | |
| | | | | | | | | | - iO |
| | | | | | | | | | |
| | | | | | | | | | |
ЛИТЕРАТУРА
1. Taig I. С, Sirucfural Analysis by (he Matrix Displacement Method, Engl. Electric Aviation Rept. K S0I7, 1961.
2. Irons B. M., Numerical Integration Applied to Finite Element Methods, Conf, Use of Digital Computers in Struct. Eng., Univ. of Newcastle, 1966.
3. Irons B. M., Engineering Application of Numerical Integration in Stiffness Method, lAIAA, 14, 2035-2037 (1966); есть русский перевод: Айронс, Инженерные приложения числеииого интегрирования в методе жесткостей. Ракетная техника и космонавтика, 4, № II, стр. 213-216 (1966).
4. Coons S. А., Surfaces for Computer Aided Design of Space Form, MIT Project MAC, AUC-TR-41, 1967.
5. Forrest A. R., Curves and Surfaces for Computer Aided Design, Сотр. Aided Design Group, Cambridge, England, 1968.
6. Murnaghan F. D., Finite Deformation of an Elastic Solid, Wiley, 1951.
7. Schied F., Numerical Analysis, Schaum Series, McGraw-Hill, 1968.
8. Kopal Z., Numerical Analysis, 2nd ed., Chapman and Hall, 1961.
9. Irons B. M., Quadrature Rules for Brick Based Finite Elements, Int. 1. Num. Meth. Eng., 3 (1971).
10. Radau, Journ. de. Meth., 3, 283 (1880).
11. Anderson R. G., Irons B. M., Zienkiewicz O. C, Vibration and Stability of Plates Using Finite Elements, Int. J. Solids Struct., 4, 1031-1055 (1968).
12. Hammer P. C, Marlowe O. P., Stroud A, H.. Numerical Integration Over Sim-plexes and Cones, Math. Tables Aids Сотр., 10, 130-137 (1956).
13. Felippa C. A., Refined Finite Element Analysis of Linear and Non-Linear Two Dimensional Structures, Structures Materials Research Rept. № 66-22, Univ. of Caliiornia. Berkeley, Oct. 1966.
9.1. Введение
Применение элементов высоких порядков, рассмотренных в двух предыдущих главах, требует некоторого обоснования. Усложнение элементов приводит к дополнительным затратам мащинного времени. Поэтому необходимо рассмотреть вопрос экономичности их использования.
На фиг. 9.1 представлены результаты расчета консольной балки с помощью'различных элементов. Сравнение результатов, показывает, что при одном и том же числе степеней свободы использование сложных элементов значительно повышает точность. Однако их применение не обязательно сопровождается пропорциональным уменьшением времени решения, так как ширина ленты матрицы для сложных элементов увеличивается, тем не менее, вообще говоря, оно существенно сокращается.
При использовании сложных элементов значительно сокращается время подготовки исходных данных. В приведенном примере три сложных элемента заменяют соответственно шесть и восемнадцать простых треугольников, поэтому в итоге приходится иметь дело с меньшим количеством элементов. Кроме того, если стороны элементов представляют собой прямые линии, координаты дополнительных узлов легко определить путем введения подпрограммы интерполирования. В результате значительно сокращается число задаваемых координат.
Использование сложных элементов не будет иметь указанных преимуществ, если процесс разбиения области на элементы автоматизирован, однако программно осуществить это трудно.
С другой стороны значительное сокращение количества элементов может привести к ухудшению аппрокси.мации реальной геометрии. В таких случаях бывает лучше использовать простые элементы.
По-видимому, самой серьезной проблемой при использовании сложных криволинейных элементов являются затраты машинного
НЕКОТОРЫЕ ПРИМЕРЫ ПРИМЕНЕНИЯ ИЗОПАРАМЕТРИЧЕСКИХ ЭЛЕМЕНТОВ ПРИ ИССЛЕДОВАНИИ ДВУМЕРНОГО И ТРЕХМЕРНОГО НАПРЯЖЕННЫХ СОСТОЯНИИ
1 ...
5 6 7 [
8 ]
9 10 11 ...
27

