Главная страница сайта  Российские промышленные издания (узловые агрегаты) 

1 ... 4 5 6 [ 7 ] 8 9 10 ... 27

прямоугольником очевидно и не нуждается в дальнейшем обсуждении.

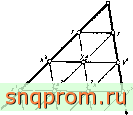
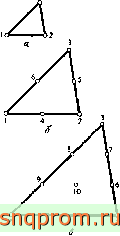
Фиг. 7.10. Семейство треугольных элементов, а -элемзнт первого порядка; б -элемент второго порядка; в -элемент третьего порядка^

i,=0

Рассмотрим ряд треугольников, изображенных на фиг. 7.10. Число узлов в каждом.элементе этого семейства таково, что

позволяет построить полный полином порядка, необходимого для обеспечения совместности между элементами. Это характерное свойство ставит семейство треугольников в привилегированное положение, так как обращение матрицы [С] всегда будет существовать [2] (см. (-7.3)]. Однако, как и ранее, пред-(х^ц 1 почтительнее прямой путь полу-чения функций формы, и, как Фиг. 7.11. L-координаты. будет показано, он достаточно прост.

Удобно ввести для треугольника специальную систему нормализованных координат.

7.7.1. L-координаты)

При рассмотрении прямоугольных элементов выбор декартовой системы координат с осями, параллельными сторонам прямоугольника, был естественным. Однако для треугольника такая система неудобна.

Для треугольника с узлами 1, 2, 3 (фиг. 7.11) удобно ввести систему координат Li, й и 1з, связанную с декартовой следующими линейными соотношениями:

у = + L2yi + Цуъ, (7.23)

Каждой совокупности координат Li, Li, La (которые не являются независимыми и связаны между собой третьим соотношением) соответствует единственная пара декартовых координат. Узел 1 имеет координаты i-i = 1, = L3 = О и т. д. Линейная связь между новыми и декартовыми координатами osHaiiaeT, что линии Li = const представляют собой прямые, параллельные стороне 2-3, на которой L\ = 0.

Легко видеть, что координату Ц точки Р можно определить как отношение площади заштрихованного треугольника к площади всего треугольника:

, площадь Р23 ,

1 - площадь 123

Разрешая соотношения (7.23), получаем ai + bix + dy

2Д

О; -I- bjX + С2У

аз -I- Ьзх + Сзу

2Д

где

1 3

= площадь 123

(7.25)

(7.26)

Отметим, что эти выражения тождественны полученным в гл. 4 [соотношения (4.56), (4.5в)].

) В оригинале Area coordinates, т. е. координагы, связанные с площадью. - Прим. ред.

7.7.2. Функции формы

Для первого элемента семейства, изображенного на фиг. 7.10, а, функции формы - просто L-координаты. Таким образом,

iV, = L N2== Li, Ыз = Ьз, (7.27)

поскольку каждая из этих координат равна единице в одном узле н нулю -в остальных узлах и изменяется линейно.

Для построения функций формы остальных элементов можно получить простое рекуррентное соотношение [2]. Предполо-

!п'0-и порядок

Фиг. 7.12. Рекуррентное правило построения функций формы для треугольников.

жим, что функции формы для треугольника я-го порядка известны. Построим функции формы для треугольника (я + 1)-го порядка. На фиг. 7.12 показаны два таких треугольника с рав-ноотстояшими друг от друга узлами. Для типичного узла i известная функция формы я-го порядка

(7.28)

выражается через L-координаты треугольника 123. Эта функция формы может быть выражена через L-координаты большего треугольника 12*3* после установления связи между координатами. Она будет принимать единичное значение в точке i и нулевое во всех остальных узлах нового треугольника, кроме узлов, расположенных на основании 2*3* треугольника. Легко показать, что

iV?+> = cLrV? (7.29)

будет искомой функцией формы, если с - масштабный множитель, обеспечиваюший единичное значение в точке ( при равенстве L * нулю на основании большего треугольника, Масштаб-

(7.30)

ный множитель задается соотношением

где / - число слоев, для которых номера узлов меньше (. Функции формы для узлов, расположенных на основании треугольника, могут быть получены простой перестановкой индексов.

Связь между этими двумя координатами ясна из фиг. 7.12, откуда видно, что

. fi+1 площадь PI3* площадь 12*3*

, п площадь Р\3

площадь 123

Следовательно,

-п площадь Р13 площадь 12*3* n+l

площадь Р\Т площадь 123

Аналогично

Ln ге-Ь 1 гп+1

и, учитывая, что ,+2 + -з=1. получаем

L?=i[( +i)/r- 1].

(7.316)

(7.31в)

Читатель может легко проверить, что приведенные ниже функции являются функциями формы для элементов второго и третьего порядков, и получить аналогичные функции для элементов более высоких порядков,

Треугольник второго порядка (фиг. 7.10,6).

Для угловых узлов

iV, = (2L,- 1)L, и т. д., для узлов на сторонах

iV4=4L,L2 и т. д.

Треугольник третьего прядка (фиг. 7.10, а|.

Для угловых узлов

jV,=y(3Z.,- 1)(3L,-2)L, и т. д..

для узлов на сторонах

(7.32)

JV4 = 11:2(31,-1) и т. д.,

(7.33)

и, наконец, для-внутреннего узла

Последняя функция обращается в нуль на границе. В гл. 10 она используется в другом смысле.

Треугольник вто.рого порядка впервые был построен Вебеке [9] и применен Аргирисом [10] для исследования плоского напряженного состояния.

При получении матриц элемента возникает проблема интегрирования по площади треугольника величин, зависящих от L-координат. Поэтому полезно иметь в виду следующее соотношение:

\ \ LXLUxdyJ,2. (7.34)

ОДНОМЕРНЫЕ ЭЛЕМЕНТЫ

7.8. Линейные элементы

До сих пор рассматривались только двумерные и трехмерные задачи. Для одномерных задач метод конечных элементов не-применялся, поскольку для них, как правило, можно получить точное решение. Однако во многих встречающихся на практике случаях могут по- требоваться и такие элементы, поэтому желательно рассмотреть их с тех же позиций, что и остальные. При решении задач упругости одномерными элементами можно аппроксимировать армирующие волокна (в двумерных и трехмерных задачах) или тонкие листовые обшивки в осесимметричных и трехмерных телах. При исследовании задач теории поля, типа рассматриваемых в гл. 15, они могут аппроксимировать дренаж в пористой среде меньшей проводимости.

. Если для элемента такого типа выбрана функция формы, то можно определить его характеристики, причем такие величины, как деформация и т. д., должны рассматриваться только в одном направлении.

На фиг. 7.13 показан такой элемент, расположенный между двумя соседними элементами третьего порядка. Ясно, что для выполнения условий совместности необходимо, чтобы функция формы была полиномом третьего порядка относительно единственной переменной . Такими функциями формы являются полиномы Лагранжа, определяемые формулой (7.15).

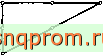
Фиг. 7.13. Линейный элемент, расположенный между двумя двумерными элементами.

ТРЕХМЕРНЫЕ ЭЛЕМЕНТЫ

7.9. Прямоугольные призмы. Сирендипово семейство [11, 12]

По аналогии с предыдущими разделами' можно построить трехмерные, элементы с дополнительными узлами. Однако теперь описанные ранее простые правила обеспечения непрерывности между элементами нужно изменить. Необходимо, чтобы изменение функции формы на грани элемента единственным образом определялось узловыми значениями. Для некоторых полиномов это можно обеспечить только подбором.

Семейство элементов, показанное на фиг. 7.14, эквивалентно семейству, изображенному на фиг. 7.4. Используя трехмерные

>?= -1

гоцзлов

32 узла

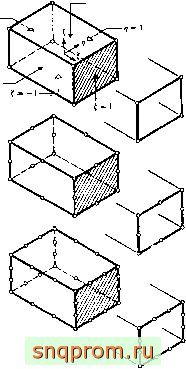
Фиг. 7.14. Правильные призтиы с узлами на границе (сирендипово семейство) и соответствующие плоские и линейные элементы.

нормализованные координаты и следуя терминологии разд. 7.3, получим следующие функции формы: Элемент первого порядка (8 узлов):

iV,=-(l+lo)(l+ria)(l+So). (7.35)

Элемент второго порядка (20 узлов): угловые узлы

iV, = I (1 + 1о) (1 + ria) (1 + to) (la + % + So - 2); (7.36) типичный узел на ребре

. = 0, Г1(=±1, £i = ±l. iV,=(l-2)(l+Ti )(l+So). , Элемент третьего порядка (32 узла): угловой узел N,==-(1+ У (1 + ria) (I + So) [9 il + vi + - 19]; (7.37) типичный узел на ребре

,= ±у, %=±1, ?,= ±1,

iV, = -- (1 - 1) (1 + 9о) (I + ria) (1 + So).

При S = I = So приведенные выражения сводятся к (7.12) - (7.14). Такие трехмерные элементы могут соединяться с плоскими или одномерными элементами соответствующего типа, как показано на фиг. 7.14.

7.10. Прямоугольные призмы. Лагранжева семейство

Функция формы для элементов показанного на фиг. 7.15 типа может быть построена в виде полинома Лагранжа. Обобщая обозначения, использованные в (7.16), запишем

iV, = L?()L7(Ti)L?(S). (7.38)

Элемент такого типа предложен Эргатудисом [6] и подробно изучен Аргирисом [7]. Все замечания относительно внутренних узлов и пределов применимости, сделанные в разд. 7.4, справедливы и здесь.

7.11. Тетраэдральные элементы

Не удивительно, что семейство тетраэдров, показанное на фиг. 7.16, обладает свойствами, сходными со свойствами семейства треугольников.

Во-первых, снова на каждом этапе используются полные полиномы от трех координат. Во-вторых, поскольку грани раз-

Фиг. 7.15. Правильная призма из лаграажева семейства.

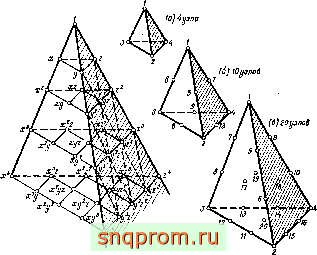
Фиг. 7.16. Семейство тетраэдров. -элемеит первого порядка; б -элемент второго порядка; з -элемент третьего порядкЗв

деляются, как и соответствующие треугольники, то в плоскости грани получается полином одинакового порядка по двум координатам и, таким образом, совместность элементов обеспечивается.

7.II.I. Пространственные L-координаты )

Введем специальные координаты (фиг. 7.17) с помощью соотношений

X = LXi + + Цхз + UXi,

у = L,!/, + Z,2(/2 -f зУз + -Уь

z = L,Zi + LiZi + z + Цг,

Разрешая эти соотношения относительно Lj, получаем выра жения типа (7.25) и (7.26), коэффициенты которых определяются соотношениями, тождественными (6.5), Координаты

(7.39)

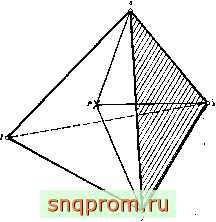
Фнг. 7.17. Пространственные -коордннаты.

точки Я представляют собой отношения объемов тетраэдров с вершиной в этой точке к объему всего тетраэдра (см., например, фиг. 7.17):

объем Р234 . >

- - объем 123Г Д- ( О)

) В оригинале Volume coordinates, т. е. координаты, связанные с объемоц. - Прим. ред.

7.11.2. Функция формы

Поскольку пространственные L-координаты связаны с декартовыми линейно и принимают значения от единицы в какой-либо вершине до нуля иа противоположной грани, то функции формы элемента первого порядка (фиг. 7.16) имеют вид

iV, = L iV2 = L2 и т. д. (7.41)

Выражения для функций формы тетраэдров более высоких порядков получаются, как и для треугольников, с помощью соответствующего рекуррентного соотношения. Оставляя его получение в качестве упражнения, приведем ряд примеров.

Тетраэдр второго порика (фиг. 7.16, б):

для угловых узлов

Af, = (2Z.,- 1)L, и т. д., (7.42)

для узлов на ребрах

ч= 4L1L2 и т. д.

Тетраэдр третьего порядка:

для угловых узлов

A/,=-i(3L,-1)(3L,-2)L, и т. д., (7.43)

для узлов на ребрах

iV5 = z L2(3L,-l) и т. д., для узлов на гранях

Ais = 27,2э и т. д. Приведем формулу интегрирования

\\\LfLUtLUxdy<iz=lll;6V. (7.44)

7.12. Некоторые другие простые трехмерные элементы

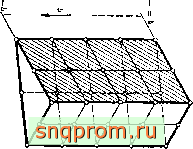
Ясно, что возможности построения элементов простых форм в трехмерном случае гораздо шире, чем в двумерном. Например, ряд элементов можно построить, исходя из трехгранной призмы (фиг. 7.18). При этом опять можно использовать ла-гранжев и сиреидипов подходы. Первые элементы обоих семейств одинаковы, и функции формы для них столь очевидны, что приводить их здесь нет необходимости.

© I

Для элемента второго порядка, изображенного на фиг. 7 . 18, б, функции формы имеют вид:

для угловых узлов (L, =,= 1)

(7.45)

iV,=L,(2L,-l)(l+S)-ii(l -а

ДЛЯ узлов на сторонах треугольников

7110 = 21,2(1+?) и т. д.. (7.46)

для узлов на сторонах прямоугольников

Mt = L{1-1) и т. д.

Сами такие элементы используются мало, но иногда находят практическое применение как составляющие сложного элемента в виде параллелепипеда с двадцатью узлами.

7.13. Заключительные замечания

В настоящей главе было описано множество различных типов элементов, причем возможности построения элементов этим не исчерпываются [4, 12]. Что же можно сказать о применении сложных элементов? За исключением треугольников и тетраэдров, все остальные рассмотренные элементы применяются только в тех случаях, когда исследуемая область может быть представленав виде некоторой совокупности правильных призм. Это очень сильное ограничение, и построение функций формы для таких элементов было бы практически бесполезным, если бы не существовало возможности деформирования элементов в соответствии с границами области. Методы деформирования в настоящее время существуют, и они будут описаны в следующей главе.

ЛИТЕРАТУРА

1. Dunne Р. С, Complete Polynomial Displacement Fields for Finite Element Methods, Trans. Roy. Aero. Soc., 72, 245 (1968).

2. Irons B. M., Ergatoudis J. G., Zienkiewicz O. C, Comment on ref. I, Trans. Roy. Aero. Soc, 72, 709-711 (1968),

3. Ergatoudis J. G., Irons B. M.. Zienkiewicz 0. C, Curved, Isoparametric, Quadrilateral Elements for Finite Element Analysis, Inf. J. Solids Struct., 4, 31-42 (1968).

4. Zienkiewicz O. C. et al.. Isoparametric and Associate Elements Families for Two and Three Dimensional Analysis, Ch. 13, in: Finite Element Methods in Stress Analysis, Holand 1., Bell K. eds., Techn. Univ. of Norway, Tapir Press, Norway, Trondheim, 1969.

5. Scott F., A Quartic, Two Dimensional Isoparametric Element, Undegraduate Project, Univ. of Wales, Swansea, 1968.

6. Ergatoudis J. G., Quadrilateral Elements in Plane Analysis: Introduction to Solid Analysis, M. Sc. Thesis, Univ. ofWales, Swansea, 1966.

7. Argyris J. Н., Buck К. E., Fried I.. Marecrek G., Scharpf D. W., Some New Elements for iVlatrix Displacement Methods, 2nd Conf. on Matrix Methods in Struct. Mech., Air Force Inst, of Techn Wright Patterson Base, Ohio, Oct. 1968.

8. Doherty W. P., Wilson E., Taylor R. L., Stress Analysis of Axisymmetric Solids Utilizing Higher-Order Quadrilateral Finite Elements. Rept, 69-3, Structural Engineering Laboratory, Univ, of California, Berkeley. Jan. 1969.

9. De Veubeke В F., Displacement and Equilibrium Models in the Finite Element Method, Ch, 9 in: Stress Analysis, Zienkiewicz 0. C, Holister G. S., eds., Wiley, 1965.

10. Argyris J. H., Triangular Elements with Linearly Varying Strain for the Matrix Displacement Method, Л Roy. Aero. Soc. Tech. Note, 69, 711-713 (Oct, 1965).

11. Ergatoudis J. G., Irons B. M., Zienkiewicz 0. C, Three Dimensional Analysis of Arch Dams and Their Foundations, Symposium on Arch Dams, Inst. Civ. Eng., London, 1968.

12. Zienkiewicz 0. C Irons B, M Campbell J., Scott P., Three Dimensional Stress Analysis, Int. Un. Th. Appl. Mech. Symp. en High Speed Computing in Elasticity, Liege, 1970.

ГЛАВА 8

КРИВОЛИНЕЙНЫЕ ИЗОПАРАМЕТРИЧЕСКИЕ ЭЛЕМЕНТЫ И ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ

8.1. Введение

В предыдущей главе было показано, как можно построить некоторые семейства элементов. Каждый новый элемент этого семейства характеризуется увеличением числа узлов и повышением точности; число таких элементов, необходимых для получения достаточно точного решения, по-видимому, будет быстро уменьшаться. На практике часто приходится рассматривать тела гораздо более сложной формы, чем в академических задачах, поэтому для аппроксимации тела относительно сложной формы небольшим числом элементов нельзя довольствоваться только простыми прямоугольниками и треугольниками. В этой главе рассматривается вопрос преобразования этих простых элементов в элементы произвольной формы.

На фиг. 8.1 и 8.2 изображены одномерные, двумерные и трехмерные элементы и соответствующие криволинейные элементы.

Здесь показано, что координаты %, ц, t, или Li, Lq, L3, L4 могут быть преобразованы в новые криволинейные координаты.

Двумерные элементы можно деформировать не только в двумерные, но и в трехмерные элементы, как показано на фиг. 8.2. При деформировании должно иметь место взаимно однозначное соответствие между декартовыми и криволинейными координатами, т. е. должны существовать соотношения типа

или /

(8.1)

Если связь между координатами известна, то, построив функции формы в локальной системе координат, после соответствующих преобразований можно определить характеристики элементов. Однако необходимо исследовать, удовлетворяют ли функции формы критериям сходимости. Можно показать, что при определенном виде преобразований координат эти критерии выполняются.

(-1, lie

	-<	>-	-<
					I <
и				>-

L, -0

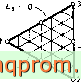
Локальные координаты

t, =0

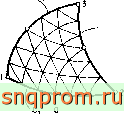
Оекартовы координаты

Фиг. 8.1. Преобразованне некоторых элементов в двумерном пространстве.

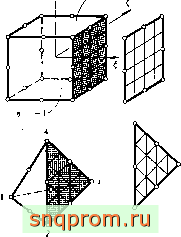
Локальные лоординаты

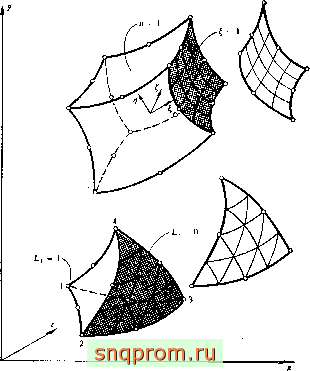
Некартовы координаты Фиг. 8.2. Преобразование некоторых элементов в трехмерном пространстве.

8.2. Использование функций формы для установления связи между координатами

Наиболее удобно для установления связи между координатами использовать функции формы, введенные ранее для аппроксимации неизвестной функции.

Если записать, например.

x = N,Xi + N2X2+ ... =liV]

(8.2)

z=N[zi + N2Zi+ ... =\N]

где \N\ - функции формы в локальных координатах, то сразу же получим искомое соотношение. Точки с координатами X\,y\,z и т. д. совпадают с соответствующими точками границы элемента (так как по определению функции формы равны единице в рассматриваемой точке и нулю в остальных).

Каждой, совокупности локальных координат будет соответствовать одна и, как правило, только одна совокупность глобальных декартовых координат. Однако далее мы увидим, что иногда при значительном деформировании взаимно однозначное соответствие может нарушиться.

Идея использования функций формы для введения криволинейных координат впервые упоминается Тайгом [I]. Он применил ее при деформировании прямоугольника в произвольный четырехугольник. Айронс [2, 3] обобщил эту идею на другие элементы.

Разрабатывая методы получения кривых поверхностей для иужд техники, к аналогичным соотношениям совершенно независимо пришел Кун [4, 5]. В настоящее время вопросы теории метода конечных элементов и исследования поверхностен становятся взаимосвязанными.

На фиг. 8.3 изображены деформированные элементы, полученные из элементов второго и третьего порядков снрендипова

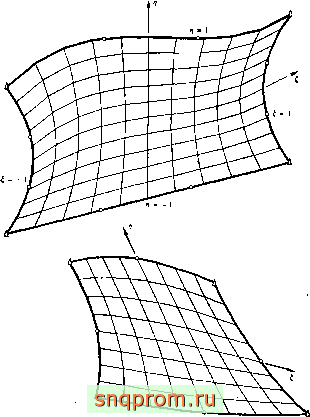
Фиг. 8 3. Построенные ЭВМ криволинейные координатные линии для элементов второго и третьего порядков (небольшое аскривлеине).

семейства. Очевидно, что между локальными (, т)) и глобальными (х, у) координатами существует взаимно одиозиачное соответствие. Если искривление элемента в некоторых точках велико, то может появиться неоднозначность, как, например, в двух случаях, показанных на фиг. 8.4. Здесь некоторые внутренние точки отображаются за пределы криволинейного элемента. Кроме того, существуют внутренние точки, которым

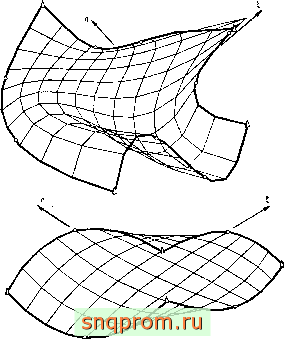
Фиг. 8.4. Чрезмерное искривление элемента, приводящее к иеоднозначностн преобразования н перегибу . Даны элементы второго и третьего порядков.

соответствуют разные локальные координаты. На практике следует избегать такого сильногоискривления.

На фиг. 8.5 приведены два примера искривления двумерного (I, ц) элемента в трехмерном пространстве (х, у, г).

Далее в этой главе часто будем называть основной элемент в недефорйированных локальных координатах первичным элементом.

8.3. Геометрическое соответствие элементов

Хотя было показано, что при использовании функции формы для преобразования координат каждый первичный элемент единственным образом отображает некоторую часть реального объекта, важно, чтобы разбиение на новые криволинейные эле-

менты не оставляло щелей между ними. Воз.можность возникновения таких щелей показана на фиг. 8.6.

Теорема 1. Если два смежных криволинейных элемента образуются из первичных, функции формы которых удовлетворяют условиям непрерывности, то они будут соприкасаться по всей границе.

Эта теорема очевидна, ибо однозначность любой функции ф, вытекающая из условия непрерывности, означает однозначность преобразования координат х, у, г. Так как координаты узлов одни и те же, непрерывность имеет место. Узлы новых искривленных элементов не обязательно располагать только в точках, для которых определены функции формы. Внутри элемента или на его границах можно ввести дополнительные узлы.

8.4. Изменение неизвестной функции в криволинейных элементах. Условия непрерывности

После построения элемента с помощью функций формы [/V] для исследования его характеристик необходимо задать вид неизвестной функции-. Удобнее всего использовать в криволинейных координатах обычное представление

Ф=т{фг,

(8.3)

где {}-набор узловых значений.

Теорема 2. Если функции формы [Щ, входящие в (8.3), в первичных координатах удовлетвор.чют условиям непрерывности ф, то и в криволинейных элементах условия непрерывности будут выполняться.

Эта теорема доказывается так же, как н теорема предыдущего раздела.

Узловые значения могут соответствовать узлам, используемым для задания геометрии элемента. Например, обозначенные кружочками на фиг, 8,7 точки используются для определения геометрии элемента. Для установления характера изменения неизвестной функции можно было использовать ее значение в точках, обозначенных квадратиками.

На фиг. 8.7, а для задания геометрии и конечно-элементной аппроксимации используются одни и те же точки. Итак, если

IN] = IN], (8.4)

т. е. функции формы, определяющие геометрию элемента и неизвестную функцию, одинаковы, то элемент называется изопа-раметрическим.

1 ... 4 5 6 [ 7 ] 8 9 10 ... 27