Главная страница сайта  Российские промышленные издания (узловые агрегаты) 

1 ... 3 4 5 [ 6 ] 7 8 9 ... 27

6.2.4. Матрицы жесткости, напряжений и нагрузок

Выражение для матрицы жесткости, определяемой в общем случае соотнощением (2.10), можно проинтегрировать точно, так как компоненты деформации и напряжения постоянны внутри элемента.

Подматрица с индексами rs матрицы жесткости имеет размерность 3 X 3 и определяется соотнощением

[UWrVmBAV, (6.15)

где V-объем тетраэдра.

Узловые силы, обусловленные начальной деформацией, записываются в виде, аналогичном (4.31):

{F}l = -lBflD]{eo}V, (6.16)

или для i-й компоненты

{Fi}:=-lBf[D]{e,} V.

Аналогичные выражения получаются для сил, обусловленных начальными напряжениями.

Фиг. 6.2. Способ разбиения трехмерного тела иа элементы типа кирпичикоЕ>,

Сходство с результатами гл. 4 очевидно, так что необходимость в дальнейших выводах отпадает. Читатель не встретит никаких трудностей при составлении вычислительной программы.

Распределенные объемные силы снова могут быть заданы их составляющими X, y, z или потенциалом объемных сил. Как и раньше, можно показать, что если объемные силы постоянны, то компоненты их результирующей распределяются по узлам элемента равномерно [см, (4,34)].

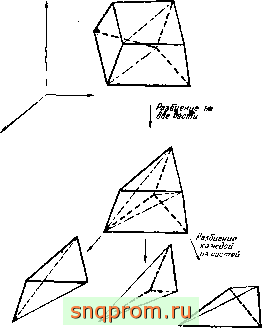
Фнг. 6.3. Составной элемент с восемью узлами и два способа разбиения его на пять тетраэдров (о и 6).

6.3. Составные элементы с восемью узлами

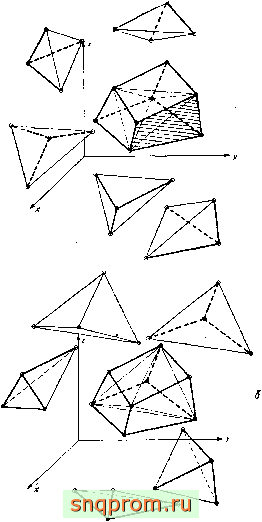
Иногда при аппроксимации объема отдельными тетраэдрами теряется наглядность, что может легко привести к ошибкам в нумерации узлов и т. д. Удобнее разбивать пространство на восьмиугольные кирпичики . Это осуществляется, как показано на фиг. 6.2, рассечением трехмерного тела параллельными плоскостями и разбиением полученных сечений на четырехугольники.

Элементы такого типа можно считать состоящими из нескольких тетраэдров, построение которых осуществляется с помощью простой логической программы. Например, как показано иа фиг. 6.3, любой кирпичик можно разделить на пять тетраэдров двумя (и только двумя) различными способами. Усреднение результатов этих двух типов разбиения приводит к незначительному увеличению точности. Напряжения хорошо представлять усредненными по всему кирпичику.

фиг. 6.4, Способ разбиения восьмиугольного кирпичика на шесть тетраэдров.

Разбиение кирпичика на шесть тетраэдров показано на фиг. 6.4. Очевидно, что существует много других возможностей.

В последующих главах мы увидим, что такое разбиение может быть полезным для построения и более сложных типов элементов.

6.4. Примеры и заключительные замечания

Простой пример применения тетраэдральных элементов показан на фиг. 6.5 и 6.6. Приближенное решение хорошо извест-

Фиг. 6.5. Задача Буссннеска как пример исследования трехмерного напряженного состояния.

Граничяые условия: и=о=ю=0 на ДЙСС, Ц AEFs} У^ tHeTpHH, вса дру. гне границы свободные.

ной задачи Буссинеска о действии сосредоточенной силы на упругое полупространство получено в результате исследования конечного объема кубической формы. Использование симметрии позволяет сократить число неизвестных и записать краевые условия для перемещений в указанном на фиг. 6.5 виде [И]. Так как нулевые перемещения заданы на конечном расстоянии от места приложения нагрузки, перед построением представленных на фиг. 6.6 графиков результаты корректировались по точному решению. Значения полученных напряжений и перемещений оказались довольно точными, хотя следует отметить, что раз-биенне было достаточно грубым. Однако даже для т9Ко(5

Сечение г = - 15см

г=-53.5см

39,г-/о^н

г=- 4см

чВьшисленное значение -Точное значение

а

-tr-

3.05

e,fo-

9./5

3.05

5,10

3.05

Фиг. 6.6. Задача Буссшнеска. й.-напряжения в вертикальном направлеыин о^; б-вертикальные перемещения tp.

рит^ммо Бвгпон

SHMBS -j t= 3,38to Н/м

= 0.15

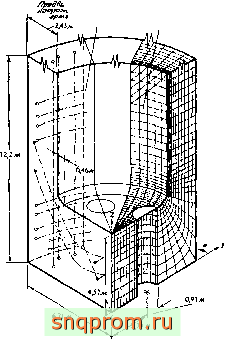
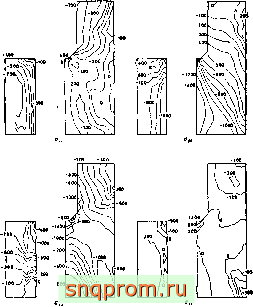
Фнг. 6.7. Расчет сосуда высокого давления реактора с использованием простых тетраэдральных элементов. Геометрия,

элементы н некоторые результаты расчета напряжений.

простой задачи пришлось решать систему из 375 уравнений. В работах [5-11] с помощью тетраэдральных элементов рассмотрены более сложные задачи. На фиг. 6.7, взятой из работы [5], приведены результаты расчета сосуда высокого давления сложной формы. В этой задаче рассматривалось около 10 000 степеней свободы. В гл. 9 буде показано, что использование более сложных элементов позволяет провести достаточно точный расчет аналогичной задачи с гораздо меньшим общим числом степеней свободы.

ЛИТЕРАТУРА

1. Gallagher R. В., Padlog J., Bijlaard P. P., Stress .Analysis of Healed Complex Shapes, ARS J., 700-707 (1962); есть русский перевод; Галлагер, Пад-лог, Бейлард, Анализ напряжений в конструкциях сложной формы, подверженных нагреву, Ракетная техника и космонавтика, 32, № 5, стр. 52- 6! (1962).

2. Melosh R. J., Structural Analysis of Solids, Proc. Amer. Sac. Civ. Eng., S. T. 4, 205-223 (Aug. 1963).

3. Argyris J. H., Matrix Analysis of Three-Dimensional Elastic Media - Small and Large Displacements, }A[AA, 3, 45-5] (Jan. 1965); есть русский перевод: Аргиряс, Матричный анализ малых и больших перемещений в трехмерных упругих средах, Ракетная техника и космонавтика, 3, № 1, стр. 177-186 (1965).

4. Argyris J. Н., Three-Dimensional Anisotropic and fnhomogeneous Media - Matrix Analysis for Small and Large Displacements, fngeniour Archiv., 34, 33-55 (1965).

5. Rashid Y. R., Rockenhauser W., Pressure Vessel Analysis by Finite Element Techniques, Proc. Conf. on Prestressed Concrete Pressure Vessels, fnst. Civ. Eng., 1968.

6. Argyris J. H., Continua and DIscontinua, Proc. Conf. Matrix Methods in Structural Mechanics, Wright Patterson Air Force Base, Ohio, Oct. 1965.

7. Irons B. M., Engineering Applications oi Numerical Integration in Stiffness Methods, JAIAA, 4, 2035-2037 (1966); есть русский перевод: Айроис, Инженерные приложения численного интегрирования в методе жесткостей. Ракетная техника и космонавтика, 4, № 11, стр. 213-216 (1966).

8. Ergatoudis J., frons В. М., Zienkiewicz О. С., Three Dimensional Analysis of Arch Dams and Their Foundations, Proc. Symp. Arch Dams, Inst. Civ. Eng., 1968.

9. Argyris J. H Redshaw J. C, Three Dimensional Analysis of Two Arch Dams by a Finite Element Method, Proc. Symp. Arch Dams, fnst. Civ. Eng., 1968.

10. FJeld S., ТЬгее Dimensional Theory of EIastics , Finite Element Methods in Stress Analysis, Holand 1., Bell K., eds., Tech. Univ. of Norway, Tapir Press, Trondheira, 1969.

U. Pedro J. 0., Thesis 1967, Laboaratorio Nacional de Engenharia Civil, Lisbon.

7.1. Введение

В предыдущих трех главах дано довольно подробное описание, как могут быть поставлены и решены задачи линейной тео^-рии упругости с помощью конечных элементов простейших форм. Хотя подробные выкладки проведены только для функций формы, относящихся к треугольным и тетраэдральным элементам, очевидно, что точно гак же можно было бы рассмотреть и другие элементы. Фактически если выбран тип элемента и определены соответствующие функции формы, то все дальнейшие действия просты, порядок их ясен и они могут быть выполнены вычислителем, не знакомым с физическим содержанием задачи. Из последующего станет ясно, что вполне возможно составить программу, позволяющую решать на машине широкие классы задач только при задании определенных функций формы. Однако выбор функций представляет собой вопрос, требующий разумного решения, в принятии которого роль человека пока является определяющей. В настоящей главе излагаются правила построения некоторых семейств одномерных, двумерных и трехмерных элементов.

В задачах теории упругости, рассмотренных в гл. 4-6, перемещения представляли собой двух- или трехкомпонентный вектор, а функции формы записывались в матричном виде. Однако функции формы строились для каждой компоненты в отдельности, и матричные выражения, по существу, получались путем умножения некоторой скалярной функции на единичную матрицу [см., например, (4.7), (5.3) и (6.7)]. Поэтому в этой главе ограничимся рассмотрением только скалярных функций формы Ni (штрихи в обозначениях опущены).

Функции формы, использованные при решении задач теории упругости в перемещениях, удовлетворяли критериям сходимости глав 2 и 3:

а) непрерывность только неизвестных должна иметь место между элементами (т. е. непрерывность угла наклона не требуется);

б) функция должна допускать выбор произвольной линейной формы, обеспечивающей постоянство деформаций (постоянство первой производной функции).

ФУНКЦИИ ФОРМЫ ЭЛЕМЕНТА. НЕКОТОРЫЕ СЕМЕЙСТВА ЭТИХ ФУНКЦИЙ

От функций формы, которые рассматриваются в этой главе, требуется только, чтобы они удовлетворяли этим двум критериям. Поэтому их можно использовать во всех задачах предыдущих глав и .в других задачах, в которых требуется выполнение только этих условий. Например, введенные здесь элементы и функции можно использовать во всех задачах гл. 15. Фактически они применимы всегда, когда в функционал / (см. гл. 3)] входят производные только первого порядка.

Семейства элементов отличаются друг от друга числом степеней свободы. Возникает вопрос: можно ли получить преимущества экономического или какого-либо другого характера, усложняя элемент путем увеличения числа степеней свободы? Ответить на него нелегко, хотя можно сказать, что, как правило, при заданной степени точности усложнение элемента приводит к уменьщению общего числа неизвестных. Однако экономичность алгоритма определяется как временем счета, так и степенью сложности подготовки входных данных. При уменьшении числа переменных может заметно увеличиться время, необходимое для получения.основных соотношений, хотя время решения уравнений при этом уменьшается.

В предыдущей главе уже упоминалось, что повышение эффективности алгоритма особенно важно при решении трехмерных задач.

Это важно и при решении других задач, поэтому в каждом конкретном случае должна быть найдена оптимальная форма элемента.

ДВУМЕРНЫЕ ЭЛЕМЕНТЫ

7.2. Прямоугольные элементы.

Некоторые предварительные соображения .

Очевидно, что (особенно, если читатель привык использовать декартову систему координат) простейшим плоским элементом является прямоугольник со сторонами, параллельными осям X VL у. Рассмотрим, например, прямоугольник, изображенный на фиг. 7.1. Здесь узловые точки пронумерованы от 1 до 8. Значения неизвестной функции ф в них представляют собой параметры элемента. Как определить функции формы для элемента такого типа?

Предположим сначала, что они являются полиномами по х и у. Для того чтобы функция ф была непрерывна между элементами, она должна изменяться вдоль верхней и нижней границ по линейному закону. Для каждого из элементов, расположенных выше или ниже рассматриваемого прямоугольника, существуют две точки, в которых функции принимают заданные зна-

чения, и, так как два значения единственным образом определяют линейную функцию, условие непрерывности выполняется во всех точках этих сторон. Это обстоятельство уже использовалось при выборе линейной функции формы для треугольника.

Аналогично если вдоль вертикальных сторон принят кубический закон изменения функции формы, то условия непрерывности на них выполняются, так как четыре значения единственным образом определяют кубическое разложение. Первый критерий при этом удовлетворяется.

Фиг. 7.1. Прямоугольный элемент.

Для того чтобы производная могла принимать любые наперед заданные значения, в разложении необходимо учитывать все линейные члены.

Так как для определения функции имеется восемь точек, в разложении можно оставить только восемь членов, т. е. можно положить

= а, + оаж + Озг/ -Ь а^ху + а^у^ + а^у^ + щур + аяху\ (7.1)

Вопрос о том, какие именно члены следует сохранить в полиноме, можно решить едиистйенным образом, если оставить члены возможно более низкого порядка, хотя мы поступили по-другому'). Читатель может легко убедиться, что теперь выполнены все необходимые требования.

Подставляя координаты различных узловых точек, получим систему уравнений для определения коэффициентов. Она запи-

) Сохранение в разложении члена высшего порядка, а не более низкого приводит обычно к несколько худшей аппроксимации, хотя сходимость прн это сохраняется (1].

сывается, как и (4.4) для треугольника, в виде

			/]. х,у\, у1 х,у\-
		.......			. 8 ,

(7.2)

(7.3) (7.4)

(7.5) (7.6)

Таким образом, функция формы для этого элемента, определяемая равенством

= [N\{j.Y={ N .... Ы^ЩУ, (7.7)

или

{ФУ={С]{а).

Отсюда получаем

н формулу (7.1) можно записать в виде

= [Р](а} = [Р][СГ{Г. [Р] = [1,, у,ху,у\ху\у',Х1\.

где

находится из соотношения

[л/] = [Р][сг.

(7.8)

Этот метод, не требующий большой изобретательности, часто используется на практике, однако он имеет существенные-недо-статки. Иногда матрица [С] может не иметь обратной [2], и, кроме того, всегда нахождение обратной матрицы в общем виде, пригодном для элементов всех конфигураций, сопряжено с преодолением значительных алгебраических трудностей. Поэтому целесообразно выяснить, нельзя ли прямо записать функции формы Ni(x,y). Прежде чем сделать это, рассмотрим некоторые общие свойства этих функций.

Некоторые важные свойства можно выявить, анализируя соотношение (7.7). Во-первых, так как это равенство справедливо для всех {фУ, то

N,= 1

в узле i н обращается в нуль во всех остальных узлах. Кроме того, должны соблюдаться законы изменения функции вдоль границ, обусловленные требованиями непрерывности (в приве-. денном примере -линейный закон по д; и кубический по у). На фиг. 7.2 в изометрии изображены функции формы для рассматриваемых элементов, соответствующие двум типичным узлам. Ясно, что их можно записать в виде произведений соответствующих функций, линейных по х и кубических-по у. Очевидно, чтд

такое простое решение, как в этом примере, возможно не всегда, однако вообще рекомендуется записывать функции формы в явном виде.

В дальнейшем удобно использовать нормализованные координаты. Такие координаты показаны на фиг. 7.3; они выбираются так, чтобы стороны прямоугольника совпадали с координатными

Фиг. 7.2. Функции формы для э.пемента, показанного иа фиг, 7.1.

				О
	£=-/	с		О
			5 = /

Фиг. 7,3, Нормализованные координаты для прямоугольника.

ЛИНИЯМИ ±1. Эти координаты связаны с координатами х я у соотношениями

(7.9)

Если функции формы известны в нормализованных координатах, то переход к первоначальной системе координат и преобразование различных выражений, встречающихся, например, при определении жесткости, тривиальны и их можно осуществить с помощью соотношений (7.9).

7.3. Прямоугольные элементы. Снрендипово семейство [3, 4]

Удобнее всего выразить функции через координаты узлов на границе элемента. Рассмотрим, например, первые три элемента, изображенные на фиг. 7.4. Количество узловых точек

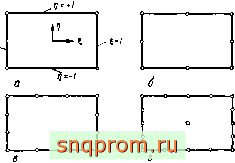
Фиг. 7.4. Прямоуго.чьипки с узлами иа границе (сирендипово семейство), о -элемент первого порядка; 6 -элемент второго порядка; в-элемент третьего порядка г -элемент четвертого порядка.

на сторонах этих элементов увеличивается, причем их число на каждой стороне одинаково. Для обеспечения непрерывности функция формы должна изменяться вдоль границ элементов а -е по линейному, параболическому и кубическому законам соответственно.

Чтобы построить функцию формы для первого элемента, отметим, что произведение

-j(l+l)(n+l) (7.10)

равно единице в верхнем правом углу, где = т)= 1, и нулю в остальных углах. Эта функция изменяется вдоль всех сторон линейно, и, следовательно, условие непрерывности выполняется. Введение новых переменных

1о = 1? , По = 11Ч< (7-И)

позволяет записать все функции формы в виде одного выражения

iV = j(l+y(l+tio). С7.12)

Так как линейная комбинация этих функций формы позволяет описать произвольный линейный закон изменений ф, второй критерий сходимости тоже удовлетворяется.

Читатель легко может убедиться, что приведенные ниже функции для элементов второго и третьего порядков удовлетворяют всем необходимым критериям.

Элемент второго порядка:

угловые узлы

= 1 (1 + 1о) (1 + Ло) Но + Т1о - 1), (7.13)

узлы на сторонах li = 0,

iVi=j(l-=)(l+4o).

iV =4(H-lo)(i-n=5.

Элемент третьего порядка: угловые узлы

(7.14)

узлы на сторонах

1, = ±1

и Т1(=±-=,

iV,=-(i-fio)(i-f)(H-4)-

Выражения для узлов на других сторонах получаются заменой переменных.

В следующем элементе этого семейства - элементе четвертого порядка [5] -добавляется центральная узловая точка, так что следует рассматривать все члены полного полинома четвертого порядка. Благодаря наличию центрального узла добавляется функция формы (1 -12) (1 - ti), которая обращается в нуль на всех сторонах.

Приведенные функции были найдены путем подбора. Получить функции формы для элементов этого семейства более

высокого порядка достаточно трудно, и требуется некоторая изобретательность. Своим названием это семейство обязано принцам Сирендипским, прославившимся своими неожиданными открытиями (Гораций Уолпол, 1754). -

Для многих практических целей могут потребоваться элементы с различным числом степеней свободы в направлениях и г]. В частности, такие элементы могут использоваться, когда в каком-то определенном направлении напряжеиия изменяются по заданному закону, а в другом - произвольно (как, например, в балке). Некоторые функции формы таких элементов, а также элементов с различным числом степеней свободы на противоположных сторонах рассматриваются в работе [2], но читатель может и сам испробовать свое мастерство для их построения.

7.4. Прямоугольные элементы. Лаграижево семейство [3, 6, 7]

Простой и универсальный способ получения функции формы любого порядка состоит в перемножении соответствующих полиномов по каждой из двух координат. Рассмотрим элемент, показанный на фиг. 7.5, в котором внутренние и внешние узлы располагаются на правильной сетке. Пусть требуется определить функцию формы для точки, обведенной кружочком. Очевидно, что произведение полинома пятой степени по \, равного единице в точках второго столбца и нулю во всех остальных узлах, на полином четвертой степени по ц, равный единице при значениях координат, соответствующих верхней строке узлов, и нулю в остальных узлах, удовлетворяет условиям непрерывности между элементами.

Полиномы от одной переменной, обладающие таким свойством, называются полиномами Лагранжа. Они записываются в виде

... (S-I.)(g-Si) . (S-;-i)(S-Si-)-i) (S -g ) (J

(Ii-li)(?i-l2)...(li-li-i)(li-li-n)..-(li-?n)

Таким образом, если пометить узел номером столбца и номером строки, на пересечении которых он расположен, то получим

Ni, = Lni)Lf(4),

(7.16)

где ft и m - количество разбиений в каждом направлении.

На фиг. 7.6 показано несколько элементов этого бесконечного семейства. Несмотря на то что такие элементы просто получить, применение их не всегда полезно не только вследствие введения большого числа внутренних узлов, но и из-за плохой аппроксимации кривых полиномами высоких порядков. Следует

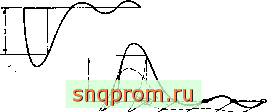
фиг. 7.5. Типичная функция формы для элемента лагранжева семейства.

о о о о

в

Фиг. 7.6. Три элемента лагранжева семейства, д -элемент первого порядка; б -элемент второго порядка; d -элемент третьего порядка.

отметить, что выражения для функций, формы содержат члены высоких порядков, тогда как некоторые члены более низкого порядка в них отсутствуют.

7.5. Внутренние узловые точки и неузловые переменные

На фиг. 7.4 и 7.6 элементы первого порядка одинаковы, а элементы второго порядка отличаются наличием центральной точки. Функции формы для двух типов элементов второго порядка приведены на фиг. 7.7.

Фнг. 7.7. Функции формы для элементов второго порядка снрендипова и лагранжева семейств.

На границах элементов эти функции однозначно определяются значениями в граничных узлах, и, следовательно, на границах они совпадают (хотя внутри элементов и существуют различия). Дополнительная степень свободы элемента лагранжева семейства описывается дополнительной функцией, умно- женной на некоторый параметр и равной нулю на границах. Этот параметр представляет собой значение функции ф в центральном узле.

Ясно, что можно построить элемент семейства Сирендипа с таким же числом степеней свободы, вводя дополнительную функцию формы, обращающуюся на границах в нуль, и умножая ее на некоторый параметр элемента ф*. Все функции формы для элементов Лагранжа можно использовать и для элементов Сирендипа, но при этом множители не соответствуют никаким узловым значениям функции ф. Множитель ф* можно назвать неузловым параметром элемента.

Минимизация функционала по такому параметру осуществляется так же, как и для внутреннего узла, ио физический смысл таких величин, как узловые силы и т. д., теперь уже не ясен. При желании каждому элементу можно поставить в соответствие несколько неузловых параметров.

Этот прием обычно не имеет больших преимуществ, так как введение неузловых параметров не изменяет функцию формы на границах.

До сих пор функции формы строились только в виде полиномов. Это имеет много преимуществ. В частности, в полином входят линейные члены, необходимые для выполнения требования постоянства производной. Однако при наличии дополнительных степеней свободы нет необходимости ограничиваться полиномами. С таким же успехом в предыдущем примере можно было бы использовать, например, функцию

cos--?cos-t), (7.17)

тождественно равную нулю на границах.

7.6. Исключение внутренних переменных при составлении ансамбля. Подконструкцин

При использовании внутренних узлов и неузловых параметров обычным путем выводятся соотношения (см. гл. 2 и 3):

= [кПФГ + {РГ.

(7.18)

Поскольку каждую из фyJкций {ф} можно разделить на две части, одна из которых {фУ связана с соседними элементами,

а другая {f} характерна только для данного элемента, можно записать

д д

и исключить {ФУ нз дальнейшего рассмотрения. Запишем (7.18) в виде

О

[кУ [к]

Ikf iw}

\{ФУ) \{РУ

(7.19) (7.20)

Из второй строки (7.19) находим

0y = -[kr4lkf{fy + {Fy)

и после подстановки этого выражения в первую строку (7.19) получаем

-1кГ{фУ+{ГУ, (7.21)

где

{гу = {РУ-[кГ1кГЧП-

Далее составляется система уравнений, содержащая лишь переменные, связанные с границами элементов, для всей области. Такой прием позволяет за счет некоторых преобразований

(7.22)

Фнг. 7.8. Сложный элемент.

на начальной стадии рассмотрения отдельного элемента существенно упростить решение системы уравнений.

Уместно дать интерпретацию такому способу исключения ноузловых переменных и провести аналогию со строительной механикой, Описанный прием, по существу, сводится к выделе-

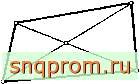
нию части конструкции и нахождению решения для этой части при заданных произвольных перемещениях на границах. Матрица [k*Y представляет полную жесткость выделенной части, а {/*) -эквивалентную систему узловых сил.

Если разбиение на треугольные элементы, показанное на фиг. 7.8, интерпретировать как совокупность шарнирно соединенных стержней, читатель без труда узнает хорошо известный прием выделения подконструкций, часто используемый в строительной механике.

Такая подконструкция, по существу, представляет собой сложный элемент, внутренние степени свободы которого исключены.

Описанный прием позволяет строить сложные элементы, которые обеспечивают получение более точного решения.

На фиг. 7.8, а изображена разделенная на треугольные элементы часть сплошной среды. Подконструк-цией в этом случае является один сложный элемент с несколькими граничными узлами (фиг. 7.8,6).

Единственное отличие таких элементов от элементов, построенных в предыдущем разделе, состоит в том, что неизвестная функция аппроксимируется не гладкими функциями формы, а набором кусочно-гладких функций. Это, по-видимому, приводит к несколько худшей аппроксимации, но зато может позволить сократить общее время расчета всей конструкции. Выделение подконструкций удобно при решении сложных задач, особенно если рассматриваемая область составлена из повторяющихся элементов.

Результаты решения простейших задач методом конечных элементов показывают, что использование сложных элементов, составленных из треугольников (или тетраэдров), приводит к лучшим результатам, чем применение простых треугольных элементов. Например, использование четырехугольника, составленного из четырех треугольников, с исключенной центральной точкой (фиг. 7.9) выгоднее использования простых треугольников. Этот и другие виды составленных из треугольников элементов подробно рассмотрены Уилсоном [8].

Фиг. 7.9. Четырехугольник, составленный из четырех простых треугольников.

7.7. Семейство треугольных элементов

В предыдущих главах в достаточной мере продемонстрированы преимущества произвольного треугольника при аппроксимации любой формы контура. Превосходство его перед

5 Зак. 613

1 ... 3 4 5 [ 6 ] 7 8 9 ... 27