Пром-Снег: Промышленность узловых агрегатов

Главная страница сайта Российские промышленные издания (узловые агрегаты)

1 2 3 4 [ 5 ] 6 7 8 ... 27

Используя функции перемещений, определенные соотношениями (5.3) и (5.4), получаем

{е} = [В] {бГ = [Ви В,. В J {6Г.

где

а, . . . с,г

дг О О

2Д

- + + -

и т. д. (5.6)

Поскольку матрица В содержит теперь координаты г и 2, деформации в элементе не будут постоянными, как в случаях плоского напряженного и плоского деформированного состояний. Это различие обусловлено членом ее. Если заданные узловые пере.мещения таковы, что и пропорционально г, то все деформации будут постоянны. Очевидно, что, поскольку только такие перемещения соответствуют постоянным деформациям, используемая функция перемещений удовлетворяет основному критерию гл. 2.

5.2.3. Начальная деформация (температурная деформация)

В общем случае должны быть рассмотрены четыре независимые компоненты вектора начальной деформации

{ео} =

вго УггО

(5.7)

Хотя, вообще говоря, начальная деформация может изменяться внутри элемента, удобно считать ее постоянной.

Возникновение начальной деформации чаще всего обусловлено тепловым расширением. Для изотропного материала в этом случае будем иметь

{8о} =

(5.8)

где 9 -средняя по элементу температура, а а - коэффициент линейного расширения.

Общий случай анизотропии материала нет необходимости рассматривать, так как при этом осевая симметрия невозможна. Некоторый практический интерес представляет слоистый материал, аналогичный рассмотренному в гл. 4, плоскость изотропии которого перпендикулярна оси симметрии (фиг. 5.3). У та-

Фиг. 5.3. Слоистый материал в случае осевой симметрии.

ких материалов возможны два различных коэффициента линейного расширения: kz в осевом направлении и кг в плоскости, перпендикулярной этому направлению.

В этом случае начальная температурная деформация имеет вид

. О .

{ео} =

(5.9)

Такая анизотропия часто встречается при исследовании деталей машин из слоистых или стекловолокнистых материалов.

5.2.4. Матрица упругости

Теперь надо получить матрицу упругости [D], связывающую деформации {е} и напряжения {о} стандартным соотношением

Or v. Т

:[D]({8}-{eo}).

Рассмотрим сначала слоистый анизотропный материал, так как матрица упругости для изотропного материала может быть получена как частный случай.

Слоистый анизотропный материал (фиг. 5.3). Полагая, что ось 2 направлена по нормали к плоскостям слоев, перепишем соотношения (4.22) (пренебрегая для удобства, как и ранее, начальными деформациями) в виде

8, = -

V =

	1 г	1%
		Ег

(5.10)

Вводя опять обозначения Е,

- = п и

и разрешая систему относительно напряжений, находим

D =-el V

(l + v,)(l-v.-2/.v)

I-v2 nv,(l+v,) rtV2(l-fv,) 0

n(l-nv2) 0

Симметрично f (l.. V)(l v,-2nv2)

(S.fl)

Изотропный материал. Для изотропного материала матрицу [D] получаем, полагая

= = £ или я = 1

V= V2=V,

а также используя известную зависимость между упругими постоянными

G2 G 1

£j ~ £ ~2(l--v)

Подстановка приведенных выше выражений в (5.11) дает

E{\-v)

(H-v)(l-2v)

1-v 1-v

Симметрично

О О

1 -2v 2(l-v)

(5.12)

5.2.5. Матрица жесткости

Матрицу жесткости элемента Цт можно составить, используя соотношение (2.10). Так как объемный интеграл берется по всей кольцевой области, получим

(5.13)

[кУ = 2л\[ВГ10] [B]rdrdz,

где матрица [В] определяется равенством (5.6), а матрица [D] - соотношениями (5.11) или (5.12) в зависимости от свойств материала.

Интегрирование теперь не удается выполнить так же просто, как в случае плоского напряженного состояния, поскольку матрица [В] зависит от координат. Существуют две возможности: первая - интегрировать численно и вторая - перемножить входящие в интеграл матрицы и затем почленно проинтегрировать.

Простейший приближенный метод состоит в определении матрицы [Б] для центра тяжести сечения элемента с координатами

-..... ; + ; + >

В этом случае первое приближение имеет вид

lk] = 2л[BY[D][B]f, где А - площадь треугольника.

(5.14)

Мо&но было бы использовать более точные методы, требующие вычисления подынтегрального выражения в нескольких точках треугольника. Такие методы будут подробно рассмотрены в гл. 8. Однако можно показать, что если используемый метод численного интегрирования позволяет точно вычислить объем элемента, то при неограниченном возрастании числа разбиений решение будет сходиться к точному [4]. Предложенное здесь одноточечное интегрирование является методом численного интегрирования именно такого типа, поскольку известно, что объем тела вращения равен произведению площади сечения на длину пути пройденного центром тяжести. Для получения достаточной точности при использовании простых треугольных элементов обычно требуется довольно мелкое разбиение, поэтому большинство созданных программ использует этот простейший метод интегрирования, который, возможно несколько неожиданно, иногда оказывается лучше точного. Причина этого состоит в том, что при точном интегрировании появляются члены, содержащие логарифмы. Под знак логарифма входят отношения типа / j/гт. Когда элемент находится на большом расстоянии от оси, величина этого отношения близка к единице и логарифм вычисляется неточно.

Если возникает необходимость в точном интегрировании, то удобно поступить следующим образом.

Как и в предыдущей главе, разобьем матрицу жесткости на отдельные подматрипы размерности 2X2 [см. соотношения (4.28) -(4.30)] вида

\KA2n\\[B,Y[D]\B,]rdrdz. (5.15)

Целесообразно выделить в подматрицах [В] постоянную и переменную части. Так, например, можно написать

[в,1 = [в,] + [вп,

(5.16)

где [Sj]- матрица [В,] для центра тяжести элемента [использованная в (5.14)], а второе слагаемое - отклонение от этой величины. Легко показать, что это слагаемое можно записать в виде

Г О От

0 о

1 о L0 0.

Подставляя эти выражения в (5.15) и замечая, что \[B\]rdrdz = [Q],

[В\] =

(ai + c,z)jr - (fl; + CjZYr 2

(5.17)

получаем

[krs] = lkrs]-\-[krsl (5.18)

где первое слагаемое в точности совпадает с (5.14), а второе - поправочный член, определяемый выражением

гО 0-1

t = wLo о о oj1

о о 1 01

0 о

1 о

L0 OJ

X \ {(а,+с,2)/г-(а,+с,2) =} {(a,+c,z)lr-{a,+CsZ)lr}rdr dz. (5.19) Если для интегралов использовать сокращенные обозначения

5drd2 = A./2, (5.20)

\~drdz = I3, то окончательно поправочный член можно записать в виде

°1х

О О

X {arus (/, - иП + (a,cs + а,сЛ (/2 - z/f) + с,с, (/3 - zr}]- (5.21)

Интегралы /j -/3 вычисляются в явном виде через узловые координаты.

5.2.6. Внешние узловые силы

В двумерных задачах, рассмотренных в предыдущей главе, вопрос определения узловых сил, обусловленных внешней нагрузкой, был настолько ясен, что не нуждался в комментариях. В рассматриваемом случае, однако, следует иметь в виду, что узловые силы изображают совокупность сил, действующих по всей длине окружности, образующей узел элемента. Это обстоятельство уже учитывалось при составлении матрицы жесткости элемента, когда интегрирование проводилось по всей кольцевой области элемента.

Следовательно, если R представляет собой радиальную составляющую силы на единицу длины окружности узла радиуса г. То в расчетах должна использоваться внешняя сила 2nrR, Аналогично сила в осевом направлений 2nrZ характеризует совокупность осевых сил.

5.2.7. Узловые силы, обусловленные начальной деформацией Снова используя (2.9), получаем

{Щ = - 2я j [Bf [D] Ы г drdz. (5.22)

Учитывая, что деформация {во} постоянна, для каждого узла можно записать

{Fi}:. = -2:i(S [Btfrdrdz)[D\{z,}. (5.23)

Интегрирование осуществляется тем же способом, что и при определении жесткости. Ясно, что опять можно использовать приближенное выражение

(5.24) (5.25)

с поправочным членом. Таким образом, имеем

Однако можно показать, что в этом случае поправочный член равен нулю, так как

{F\}1 = 2:1 (5 [ВП г dr dz) [D] {е„} = 0.

поэтому представление

{F.r=-2n[Bf[D] {e,}r

(5.26)

является точным. Силы, обусловленные начальными напряжениями, определяются таким же образом.

5.2.8. Распределенные объемные силы

При рещении осесимметричных задач часто возникает необходимость рассматривать распределенные объемные силы, такие, как сила тяжести (если она действует вдоль оси г), центробежная сила во вращающихся механизмах, внутреннее давление в пористом материале.

Запишем такие силы в виде вектора

(5.27)

где R, Z - компоненты силы в направ.лениях гиг соответственно на единицу объема материала. В соответствии с (2.11) имеем

{F}l==-2n\[N\{}rdrdz,

или для 1-го узла

{Fi};=-2n\{}mrdrdz:

(5.28)

Если в первом приближении допустить, что объемные силы постоянны, то с помощью переноса начала координат, так же как в подразд. 4.2.7, легко получить

{Fdl = (Fi); = [Fm]; = - 2я { I} -f -. (5.29)

Хотя это выражение не совсем точно, можно показать, что величина поправочного члена уменьшается с уменьшением размеров элемента и вследствие самоуравновешенности он не приведет к заметной ошибке. Ясно, что в случае необходимости интегрирование в (5.28) можно произвести точно.

Если объемные силы заданы потенциалом, аналогичным введенному в подразд. 4.2.8, т. е.

--~дГ

Z= -

(5.30)

и если этот потенциал линеен относительно своих узловых значений, то можно использовать выражение, эквивалентное (4.40).

Во многих задачах объемные силы пропорциональны расстоянию г от оси симметрии. Например, во вращающемся теле

(5.31

где и -угловая скорость, а р - плотность материала. Очевидно, что аппроксимация (5.29) в этом случае будет очень грубой, и для получения хорошего результата необходимо точное интегрирование.

5.2.9. Вычисление напряжений

Как следует из формул (5.5) и (5.6), напряжения не постоянны внутри элемента. В этом случае удобно усреднять напряжения и относить их к центру тяжести элемента. Матрица напряжений, получающаяся из формул (5.6) и (2.3), имеет, как обычно, вид

{дГ = [0][В] {бГ - [D1 {во} + {его}.

Можно показать, что значения напряжений несколько колеблются от элемента к элементу и усреднение узловых, напряжений позволяет улучшить результат,

4 Зак, 61?

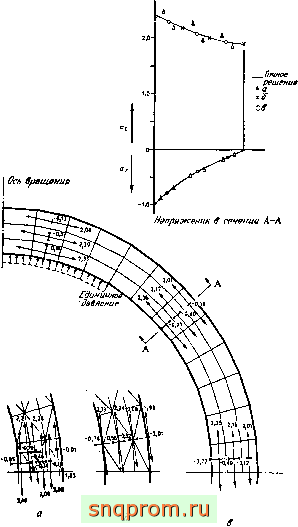
Фиг. 5.4. Напряжения в сфере при действии внутреннего давления (коэффициент Пуассона v = 0,3). а - Треугольные элементы - эначеиин в центрах тяжести; б -треугольные элементы--усреднение по узлам; в -четырехугольные элементы-усреднение по смежным треугольникам.

V Вь-тсленное значоние5,

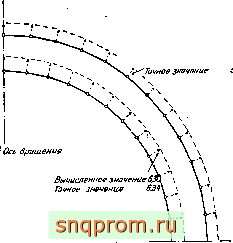
Фиг. 5.5. Перемещения внутренней и внешней поверхностей сферы при показанном на фнг. 5,4 нагруженнн.

-422

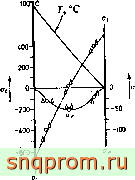
Фиг 56 Сфера прн установившемся распределении температур (100 °С на внутренней поверхности и 0° на внешней).

Г=%о™ о?Ж Гу?рГн?и^ угольиикои. 1- четырехугольникам.

5.3. Некоторые примеры

Решения тестовых задач, таких, например, как задачи о цилиндре с постоянными осевыми или радиальными напряжениями, как и следовало ожидать, совпадают с точными. Это очевидное следствие того, что функция перемещений может описывать однородные деформации.

Задача о сфере под действием внутреннего давления, для которой характерно почти линейное изменение напряжений, имеет точное решение. На фиг. 5.4, а показаны отнесенные к центрам тяжести элементов напряжения, полученные при использовании достаточно крупной сетки. Следует отметить, что полученные напряжения несколько колеблются около точного решения. (Эти колебания становятся еще более заметными при больших значениях коэффициента Пуассона, хотя точное реше-

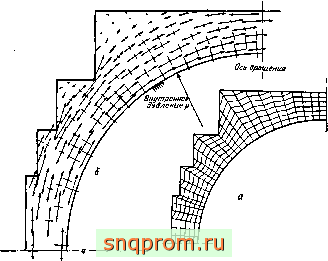
Фнг. 5.7. Сосуд реактора высокого давления, й-использованные прН расчете четырехугольные элементы, разбиение на элементы осуществлялось ЭВМ автоматически; б-напряжения при равномерно распределенной даале-НИИ р (чертеж, выполненный ЭВМ). При решении определялись средние по четырехуголь-аикам значения. Коэффициент Пуассона v=0.I5.

ние не зависит от него.) На фиг. 5.4,6 приведено гораздо лучшее приближенное решение, полученное усреднением значений напряжений в узловых точках; с помощью усреднения, результаты которого приведены иа фиг. 5.4, в, решение можно еще

улучшить. Хорошее совпадение с точным решением даже при использовании весьма грубого разбиения свидетельствует о высокой точности метода. На фиг. 5.5 с точным решением сравниваются перемещения узловых точек.

На фиг. 5.6 показаны температурные напряжения в той же самой сфере, вычисленные для установившегося температурного поля. Сравнение с точным решением снова показывает высокую точность метода.

5.4. Практические приложения метода

В этом разделе приводятся два примера практического применения метода к исследованию осесимметрического нагружения.

Оса симметрии

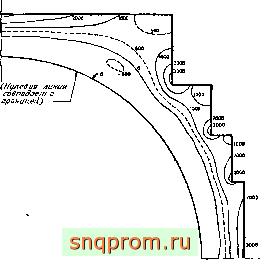
Фиг. 5.8. Сосуд реактора высокого давления. Температурные напряжения в установившемся состоянии. Линии максимальных главных напряжений (фунт/дюйм), (Температура внутри 400°С, снаружи 0°С, а = 5-10 1ГС, е = 2,58-10* фунт/дюйм , v = 0,15.)

Реактор из предварительно напряженного железобетона под давлением. На фиг. 5.7 показано распределение напряжений в упрощенном варианте такого реактора. Вследствие симметрии рассматривается только одна его половина. Приведены

сваи = 600 vceau =0,25

2 Радиус сваи-LS* I Л?г?яа сваи

Масштаб длины.

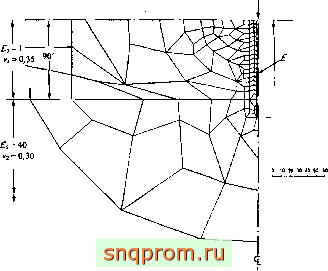
Фиг. 5.9а, Свая в слоистом грунте. Нерегулярное разбиение и исходные данные.

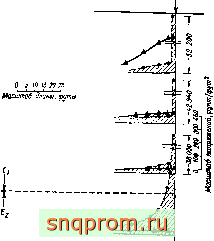
Фиг. 5.96, Свая в слоистом грунте График вертикальных напряжений в горизонтальных сечениях Показано также решение задачи Буссииеска при Е\ =

= Ei = Eosai и проведено сравнение с точным решением. - точное решение задачи Буссииеска; А решение задачи Буссинеска методом конечных элементов; решение вадачн о свае методом конечных элементов^

напряжения, возникающие при действии внутреннего давления. Аналогичные результаты легко получить для случая предварительно напряженной арматуры, если в узловых силах учесть нагрузку от арматуры.

На фнг. 5.8 приведены линии равных максимальных главных температурных напряжений. Температурные напряжения и само температурное поле в установивщихся условиях определены с помощью метода конечных элементов, как описано в гл. 15.

Свая фундамента. На фиг. 5.9а и 5.96 показано распределение напряжений вокруг сваи фундамента, проходящей через два различных пласта грунта. Решение этой неоднородной задачи не представляет трудностей и получается с помощью стандартной программы.

5.5. Несимметричное нагружение

Метод, изложенный в настоящей главе, может быть распространен на случай несимметричного нагружения. Если изменение нагрузки по окружности описывается с помощью круговых гармоник, то можно рассматривать только одно осевое сечение, хотя число степеней свободы при этом увеличивается до трех.

Некоторые детали метода описаны в гл. 13. В работе [5] можно найти полное его изложение.

ЛИТЕРАТУРА

1. Clough R. W., Ch. 7 in: Stress Analysis, Zienkiewicz 0. C, Holister G, S eds Wiley, 1965,

2. Clough R, W Rashid Y., Finite Element Analysis of Axi-Symmetric Solids, Proc. ASCE, 91, EM.l, 71 (1965),

3. Timoshenko S., Goodier J, N., Theory of Elasticity, 2nd ed McGraw-Hill, 1951.

4. Irons B. M., Comment on Stiffness Matrices for Sector Element, Raju t, R Rao A. K., JAIAA, 7, 156-157 (1969); есть русский перевод: Айронс, Замечание к статье Матрицы жесткости элементов в форме сектора . Ракетная техника и космонавтика, 8, № 3, стр. 271 (1970),

Б. Wilson Е. L., Structural Analysis of Axi-Symmetric Solids, JAIAA, 3, 2269- 2274 (1965); есть русский перевод: Вильсон, Расчет на прочность осесимметричных тел, Ракетная техника и космонавтика, 3, № 12, стр. 124-132 С1У65).

6.1. Введение

Метод конечных элементов применяется и для решения трехмерных задач. Такие задачи охватывают почти все практические случаи, хотя иногда предположение о том, что напряженное или деформированное состояние двумерно, дает вполне приемлемую и более экономичную модель .

Простейшим элементом для двумерных задач был треугольник. В трехмерном случае его аналогом является тетраэдр - элемент с четырьмя узлами. В настоящей главе будут рассмотрены основные характеристики этого элемента. Трудность, не встречавшаяся ранее, состоит в порядке индексации узлов, т. е. в построении конечно-элементной модели тела.

Впервые тетраэдральный элемент предложили использовать Галлагер и др. [1] и Мелош [2]. Позднее Аргирис [3, 4] подробно разработал этот вопрос, а Рашид [5] показал, что с помощью больших современных ЭВМ могут бытб решены поставленные таким образом практические задачи. Очевидно, однако, что для получения заданной степени точности количество простых тетраэдральных элементов должно быть очень большим. Это приводит к огромному числу уравнений, что несколько ограничивает на практике применение метода. Кроме того, ширина ленты матрицы основной системы уравнений становится большой и в результате увеличивается необходимый объем памяти вычислительной машины.

Чтобы представить себе степень сложности такого рода задач, предположим, что точность аппроксимации двумерных задач треугольными элементами сравнима с точностью аппроксимации - трехмерных задач тетраэдрами. Если, например, для достижения заданной точности при определении напряжений в квадратной двумерной области требуется сетка размерности 20 X 20, т. е. надо рассмотреть 400 узловых точек, то число уравнений для определения двух компонент перемещений каждого узла будет около 800. (Это вполне приемлемая цифра.) Лента матрицы системы содержит 20 узлов (см. главу, посвященную методам вычислений), т. е. около 40 переменных.

Эквивалентная трехмерная область представляет собой куб с 20 X 20 X 20 = 8000 узловых точек. Так как теперь должны

быть определены три компоненты перемещений в каждой узловой точке, общее число уравнений достигает 24 000, а лента матрицы содержит 20 X 20 = 400 взаимосвязанных узлов, т. е. 1200 переменных.

Если учесть, что вычислительные трудности при использовании обычных методов решения, грубо говоря, пропорциональны количеству уравнений и квадрату ширины ленты матрицы, то нетрудно представить себе сложность решения таких задач. Не удивительно поэтому, что попытки уточнить решение трехмерных задач связаны в основном с использованием сложных элементов, обладающих большим числом степеней свободы [6-10]. В последних главах будут приведены примеры практического применения таких элементов. Эта глава содержит все необходимые сведения для постановки трехмерных задач теории упругости. Обобщение на случай более сложных элементов не вызовет затруднений.

6.2. Характеристики тетраэдрального элемента 6.2J. Функции перемеи^ений

На фиг. 6.1 изображен тетраэдральный элемент Црт в системе координат х,утлг.

Перемещение любой точки определяется тремя компонентами и, и и ьу в направлениях координат х, у к z. Таким образом, вектор перемещений имеет вид

(6.1)

Если для задания линейного закона изменения какой-либо величины в плоском треугольном элементе требовались три узловых значения, то в трехмерном случае необходимо задать четыре узловых значения. По аналогии с представлением (4.3) можно записать, например,

= а, -f ttiX + щу -f 042.

(6.2)

Приравнивая эти выражения перемещениям узловых точек, получаем четыре уравнения типа

u; = а, -f a2Xi -f ayi + aZi и т. д., fi3 которых определяются коэффициенты а.\ - щ.

(6.3)

ИССЛЕДОВАНИЕ ТРЕХМЕРНОГО НАПРЯЖЕННОГО СОСТОЯНИЯ

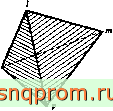
Фиг. 6.1. Тетраэдральный элемент. (Прн нумерации узлов следует придерживаться определенного порядка, начиная, например, с точки р, остальные узлы нумеруются в направлении против часовой стрелки по отношению к ней - рЦт ели mipi и т. д.)

Запишем теперь соотношение (6.2) в форме, аналогичной (4.5), с использованием определителя

и == bF i -bix-\-c,y-\- diz) щ + + (a; + Ъ,х + c,y + d,z) и, +

+ (яр + М + <рУ + dpz) Up),

где

6У = det

1 Xi yi Zi

1 X, у, Zi

1 Xm Ут Z

1 Ур Zp

(6.4)

(6.5a)

Величина в данном случае представляет собой объем тетраэдра. Коэффициентами а;, С;, d( обозначены определители

О; = det

Ci = -det

&, = -det

d, =--det

I 2 1

1 Ур

XI У1

Xm Ут.

Xp Ур

(6.56)

Остальные коэффициенты получаются циклической перестановкой индексов р,!, /, т.

Как видно из фиг. 6.1, узлы р, /, /, m пронумерованы в соответствии с правилом правой руки, причем первые три узла пронумерованы по часовой стрелке, если смотреть со стороны последнего узла.

Перемещение элемента определяется двенадцатью компонентами перемещений его узлов:

(6.6)

где

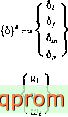
и т. д.

Перемещение произвольной точки можно записать в виде

{nVNi.INi, INm,INp]{<,Y, где скалярные величины определяются соотношениями

Ni=-- и т. д.,

(6.7)

(6.8)

а / - единичная матрица размерности 3X3.

Ясно, что эти функции перемещений будут удовлетворять требованиям непрерывности на границах между элементами. Этот результат является прямым следствием линейного закона изменения перемещений.

6.2.2. Матрица деформаций

В трехмерном случае учитываются все шесть компонент деформации. Используя известные обозначения Тимошенко, запишем матрицу деформаций в виде

{е} =

8г Уху Ууг Угх

ду ду dw ~дТ

ди . dv ду + дх

ду , дт dz df dw , ди дх f дг

(6.9)

С помощью соотношений (6.4) -(6.7) легко убедиться, что.

где

{е} = [В]{бГ = [ВьВ/, Вь. Вр]{бГ.

(6.10)

[В,] =

дЫ\ 1г

dN, ~di

dNi ~дг

dN\ ду dN. ~дГ.

(6.11)

Остальные подматрицы получаются простой перестановкой индексов.

Начальные деформации, такие, как обусловленные тепловым расширением, можно записать обычным образом в виде шести-компонентного вектора, имеющего, например, для изотропного

теплового расширения прЬстой вид;

{е } =

(6.12)

где а - коэффициент линейного расширения, а б'-средняя по элементу температура.

6.2.3. Матрица упругости

В случае материала с анизотропией свойств матрица [/)], связывающая шесть компонент напряжения с компонентами деформации, может содержать не более чем 21 независимую постоянную (см. подразд. 4.2.4).

В общем случае

{а} =

= [D]({e}-{e }) + {a }.

(6.13)

Так как такое умножение никогда не выполняется в явном виде, запишем здесь матрицу [D] только для изотропного материала, хотя это нетрудно сделать и для случая произвольной анизотропии. При использовании обычных упругих постоянных: модуля упругости Е и коэффициента Пуассона v - матрица имеет вид

mi - g<-v)

I J (l + v)(l-2v)

1 - v

Симметрично

1 -2v 2(1-v)

0 0 0

1 -2v 2(1 -v)

0 0 0

1 - 2v 2(l-v)

(6.14)

1 2 3 4 [ 5 ] 6 7 8 ... 27