Главная страница сайта  Российские промышленные издания (узловые агрегаты) 

1 2 3 [ 4 ] 5 6 7 ... 27

Расчленяя это соотношение, можно записать

{Pi}l=-\Btf[D\[Eo]t и т. д. (4.32)

Силы, обусловленные начальной деформацией, распределяются по узлам элемента неравномерно и должны быть вычислены точно. Аналогичные выражения получаются для сил, обусловленных начальными напряжениями.

4.2.7. Распределенные объемные силы

В общем случае плоского напряженного или деформированного состояния на каждый элемент единичной площади в плоскости X, у действуют силы

в направлениях соответствующих осей.

В соответствии с (2.11) вклад этих сил в узловые силы определяется выражением

{Fn-\[Mf[y]dxdy, или, на основании (4.7),

{!b = -{y}S(rfrfy и т. д., (4.33)

при условии, что объемные силы X и У постоянны. Так как Л^ не является постоянной, должно быть выполнено интегрирование. Некоторые общие формулы интегрирования для треугольника приведены в приложении HI.

Если за начало координат выбран центр тяжести элемента, вычисления упрощаются. В этом случае

{xd.xdy-ydxdy = 0,

И, используя (4.8), получаем

{Fi}p-[y}\aidx dyl2S = -{y} /2. ИЛИ, учитывая примечание на стр. 62, имеем

(4.34)

Ясно, что для всякого элемента

(4.35)

Это означает, что все объемные силы, действующие в направлениях хну, распределены между тремя узлами поровну. Этот факт не противоречит физическому смыслу и часто неявно использовался.

4.2.8. Потенциал объемных сил

Во многих случаях объемные силы определяются через потенциал объемных сил f в виде

]Г = -

дФ Зу

(4.36)

и чаще не значения X и У, а именно этот потенциал известен по-всюдТв области и считается заданным в узловых точках Если {} содержит три значения потенциала в узлах элемента, т. е. имеет вид столбца

fi 1

(4.37)

то в случае постоянных К и У потенциал должен изменяться внутри элемента по линейному закону. Фун^ия ФоР^ него очевидно, может быть построена, как и ранее [см. (4.4)-

[NlN N.mY- (4-38)

Следовательно,

х = -y = -

[bj, Ь Ь„] {ФУ 2Д

дФ [Oj, с,. g ] W

ду ~ 2Д

(4.39)

Вектор узловых сил, обусловленных потенциалом объемных сил, будет описываться соотношением

{П? = : г (4.40)

	bi

заменяющим (4.35).

4.2.9. Вычисление напряжений

Полученные формулы дают возможность составить полную матрицу жесткости конструкции и получить решение для перемещений.

Матрица напряжений, определяемая в общем виде равенством (2.15), получается для каждого элемента после соответствующих подстановок.

По предположению напряжения постоянны внутри элемента. Обычно их приводят к центру тяжести; это будет сделано и в большинстве примеров этой главы. Иногда значения напряжений в узлах получают усреднением напряжений в смежных элемента. Кроме того, имея некоторый опыт, можно использовать и метод усреднения с весом , но он не намного лучше.

Обычно с помощью ЭВМ определяются главные напряжения и их направления в каждом элементе.

4.3. Примеры. Оценка тонкости

Не вызывает сомнения, что решение плоских задач теории упругости методом, изложенным в разд. 4.2, при неограниченном уменьшении размеров элементов стремится к точному. Однако при любом конечном числе разбиений это решение будет приближенным, как, скажем, решение в виде ряда Фурье с ограниченным числом членов.

Как уже объяснялось в гл. 2, приближенное значение полной энергии деформации всегда будет ниже истинного значения, соответствующего точному решению. Практически это означает, что полученные перемещения, а следовательно, и напряжения будут в целом заниженными. Однако следует подчеркнуть, что все это не всегда справедливо для каждой отдельной точки сплошной среды. Поэтому практическое значение такой оценки невелико.

при разном числе разбиении.

TovHoe решение л =0,15

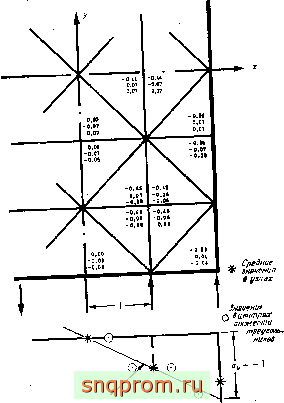
Ф.. 4.4. Результат. Р- Г Tsaaetn н^

грубом разбиении -\;lll7 .3,..L порядке.)

При наличии опыта инженер может заранее оценить порядок точности результатов для данной конкретной задачи при заданном числе разбиений. Некоторый такой опыт, вероятно, можно приобрести, изучая примеры, приведенные в этой книге.

Сначала рассмотрим некоторые простые задачи, для которых известны точные решения.

Одиородиое поле иапряженин. В этом случае решение, полученное методом конечных элементов, будет полностью совпадать с точным решением независимо от числа разбиений.

Фиг. 4.5. Круглое отверстие в области однородного напряженного

состояния.

Очевидно, что этот результат следует из постановки задачи, но тем не менее он полезен для первоначальной проверки вычислительных программ.

Линейно изменяющееся поле напряжений. В этом случае предположение о постоянстве напряжений внутри элементов означает, что решение всегда будет приближенным. На фиг. 4.4 в качестве примера представлены результаты расчета при довольно грубом разбиении балки, работающей в условиях чистого изгиба. Видно, что осевые напряжения а^, полученные методом конечных элементов, берут в вилку точное решение. Если постоянные по элементам значения напряжений отнести к центрам тяжести элементов и нанести их на график, то прямая, наименее отклоняющаяся от этих точек, фактически является точным решением.

Компонента напряжения в горизонтальном направлении и напряжение сдвига отличаются от точных (нулевых) значений-они колеблются около них с небольшой амплитудой.

Можно убедиться, что если напряжения во внутренних узлах вычисляются как средние по примыкающим к ним элементам, то они очень мало отличаются от точных. Однако на внешних поверхностях усреднение дает несколько худшие результаты. Усреднение напряжений в узловых точках часто применяется для уточнения приближенного решения (фиг. 4.4).

Для уточнения решения в узловых точках, расположенных вблизи поверхности конструкции, можно использовать усреднение с весом. Нам, однако, кажется, что для получения большей

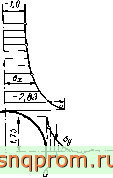
Фиг 4 6 Сравнение теоретических результатов с результатами решения методом конечных элементов задачи, иллюстрированной на фиг..Ь. о-изотропный материал; 6 -ортотропный материал. Я^=£, - -

=0, е =0,42.

- точное решение для бесконечноВ пластнньц 0 решение, полученное методом конечных элементив.

точности целесообразнее производить разбиение на более мелкие элементы.

Коицеитрация напряжений. На фиг. 4.5. и 4.6. иллюстрируется тестовая задача о концентрации напряжений. Исследуется распределение напряжений вокруг круглого отверстия в изотропном и слоисто-анизотропном материалах в условиях однородного напряженного состояния вдали от отверстия [6]. Чтобы можно было лучше изучить область, в которой ожидаются большие градиенты напряжений, используется неравномерное разбиение. Сравнение некоторых результатов расчета с точными решениями [3, 7] (фиг. 4.6) позволяет сделать вывод о высокой точности метода.

4.4. Некоторые практические приложения

элe?Pнтni n; возможности применения метода конечных элементов практически безграничны. В настоящее время при истедовании плоских задач этот метод благодаря своей вь со

няет ~1 ?т УНерсальности часто заме-

няет эксперимент. Преимуществами метода являются простота

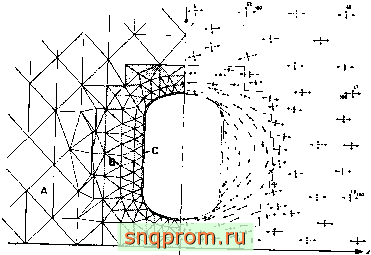
Фиг. 4.7. Подкрепленное отверстие в пластине.

Вдали от отверстая однородное напряженное состояние а^ =101}. ст-=5Э, Толщины областей пластины Л, В и С относятся как I :3; 23. (Перемещение в налравленвн 1/ на осн л

равно нулю.)

учета анизотропии свойств материала, а также легкость решения задач о температурных напряжениях и задач о действии объемных сил.

Ниже будет приведено несколько примеров применения метода к решению сложных инженерных задач.

Распределение напряжений около подкрепленного отверстия (фиг. 4.7). В стальных сосудах высокого давления или на несущих поверхностях самолетных конструкций часто приходится делать различные отверстия. Входящий трубопровод сам несколько подкрепляет отверстие, и, кроме того, для уменьшения напряжений, возникающих из-за эффектов концентрации, стенка вблизи отверстий обычно утолщается.

Исследование таких задач в плоской постановке не вызывает затруднений. Выбор размеров элементов и их расположение определяются характером изменения толщины.

Узкий утолщенный слой материала вблизи края отверстия можно аппроксимировать специальными элементами балочного типа или просто обычными треугольными (сильно вытянутыми) элементами. В задаче, иллюстрированной на фиг. 4.7, использовался последний способ, позволивший изучить распределение напряжений вблизи отверстия. Отметим, что исследовалась область сравнительно больших размеров и при решении применялось неравномерное разбиение.

Тектонические напряжения в анизотропной долине [6] (фиг. 4.8). Рассматривается симметричная долина, находящаяся под действием однородных напряжений в горизонтальном направлении. Порода состоит из различных слоев; следовательно, материал трансверсально изотропен с изменяющимися от точки к точке направлениями слоев.

Анализ полученных напряжений указывает на существование области растяжения. Это явление представляет интерес для геологов и инженеров, занимающихся механикой горных пород.

Плотина под действием внешнего и внутреннего давлений воды [8, 9] (фиг. 4.9). Исследуется опорная плотина на сложном скалистом основании. Неоднородное основание находится в условиях плоской деформации, а сама плотина рассматривается как пластина переменной толщины (плоское напряженное состояние).

Исследование нагружения внешними силами н собственным весом не ставит новых проблем, хотя, возможно, следует отме- тить, что оказалась полезной автоматизация расчета узловых нагрузок, вызванных силой тяжести.

Некоторого разъяснения требует случай действия внутреннего давления в порах.

Хорошо известно, что в пористом материале давление воды действует на конструкцию в виде объемной силы величиной

И ЧТО в этом случае нет необходимости рассматривать внешнее давление.

Давление в порах р, как это следует из формулы (4.36), является потенциалом объемных сил. Разбиение рассматриваемой области и тела плотины на элементы показано на фиг. 4.9. На фиг. 4.10, а и б приведены значения напряжений, возникающих под действием силы тяжести (учитывается только собственный вес плотины) и давления воды, которое рассматривается либо как внешняя нагрузка, либо как внутреннее давление в порах.

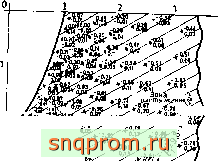
--- -0,05

, о 1

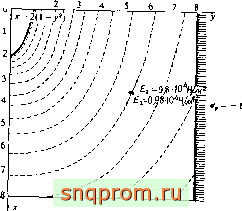
и = о исрледиемая ооласть

Фиг. 4.8. Долина с искривленными слоями под действием тектониа -кппп , пряжения в горизонтальном направлении (плкаГдф^ормарло:; 298 элементов).

Толщина стенки коитрдзарса г.75м

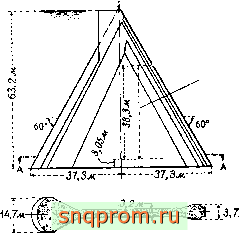
Постоянная конусность стенки /м на 82,5м

Сечение А-А в плане

а

Предполагается отсутствие переме щениа

Трещина : (не накладывается никаких ограни-\ чениа)

Гравий E=,iEc

тныи песок =£J,

Предполагается отсутствие перемещении

Фиг. 4.9. Расчет напряжений в контрфорсной плотине. Предполагаются плоское

напряженное состояние плотины и плоская деформация основания, й-сечение рассчитываемого контрфорса: б-рассчитываемый участок основания п конечные элементы.

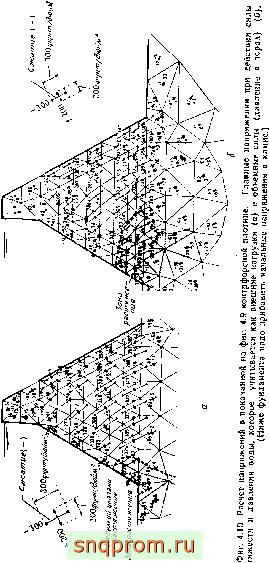
Оба решения указывают на наличие больших областей растяжения, но очень важно отметить, что во втором случае уровень напряжений выше.

Растрескивание. В приведенном примере растягивающие напряжения, без сомнения, вызовут образование трещин в породе. Если процесс распространения трещины устойчив, то можно считать, что плотина в безопасности. Наличие трещин

Сжатие(-)

Верхний Sbej> Зона растяжения

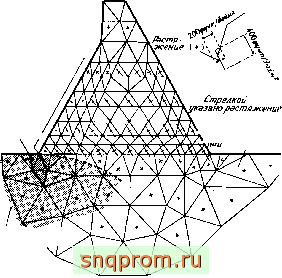
Зона растрескивания, (Е-0)

Напряжения Ses i/vema начальных напрдже- в основании

Зона растд-~\ 1 жения, не правы- I тающего верояг наго начального сжатия

Фиг. 4.11. Напряжения в контрфорсной плотине. Введение в расчет трещины меняет распределение напряжений (нагружеиие такое же, как на фиг. 4.10,6),

легко учесть в расчете, если приравнять нулю упругие постоянные соответствующих элементов. На фиг. 4.11 показана расчетная схема и результаты расчета при наличии клинообразной трещины у края плотины. Видно, что при таком размере трещины в теле плотины не возникает никаких растягивающих напряжений.

Более подробно исследование распространения трещин и связанного с ним перераспределения напряжений будет описано ниже (см. гл. 18).

Температурные напряжения. В качестве примера расчета температурных напряжений рассматривается та же плотина при

Температура изменяется -

измен, линейно

Сжатие {-) <

в основании температура не изменяется

Фиг, 4.12. Расчет напряжений в контрфорсной п-тетине. Температурные напряжения при охлаждении заштрихованной области до -9,44 С

(£ = 2.02-10 Н/м2, а = 1,08-10-6 1/°С).

Уровень воды

Локальный I. юруят-м -Ж^Гэтд прваваритв/1ьиого i - *5Г^ напряжемш

4. \}ipijHm

Р 10 fymi/

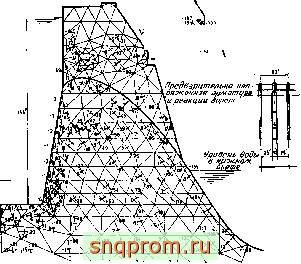
о 20 40 60 10 108 уг

фиг, 4,13, Большая водоподъемная плотина с быками и предварите.тьно напряженной арматурой.

довольно простом распределении температур. Результаты расчета приведены на фиг. 4.12.

Гравитационные плотины. Расчет опорной плотины является характерным примером применения метода конечных элементов. Несложно рассмотреть и другой тип плотины - гравитационную плотину с быками или без них. На фиг. 4.13 приведены результаты расчета большой плотины с быками и подъемными затворами.

Ясно, что в этом случае аппроксимация напряженно-деформированного состояния в окрестности резкого изменения геометрии сечения, т. е. в области, где быки соединяются с телом плотины, двумерным состоянием сомнительна. Однако она приводит лишь к локальным ошибкам.

Здесь иажно отметить, что для одновременного изучения концентрации напряжений в местах крепления тросов и распределения напряжений в плотине и в основании используются элементы разных размеров. Линейные размеры элементов относятся как 30: 1 (самые большие элементы, использовавшиеся для исследования основания, на рисунке не показаны).

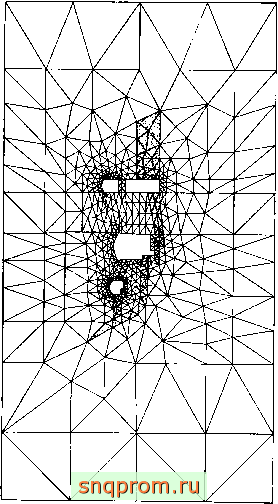
Подземная электростанция. Этот пример, иллюстрированный на фиг. 4.14 и 4.15, демонстрирует возможности метода. Главные напряжения вычерчиваются ЭВМ автоматически. Расчеты проводились при различных начальных напряжениях {оо), что связано с неточностью знаний геологических условий. Возможность быстрого решения задачи и представление результатов в виде графиков позволили оценить границы изменения напряжений и принять техническое решение.

4.5. Особенности исследования плоского деформированного состояния в несжимаемом материале

Следует отметить, что соотношение (4.20), определяющее матрицу упругости [D] для изотропного материала, теряет смысл, если коэффициент Пуассона становится равным 0,5, так как при этом знаменатель обращается в бесконечность. Эту трудность можно просто обойти, если в расчете использовать значения коэффициента Пуассона, близкие к 0,5, но не равные этой величине. Однако опыт показывает, что такой прием ухудшает решение. Геррманн [10] предложил другой метод, связанный с использованием нового вариационного принципа. Подробно этот метод изложен в упомянутой работе.

ЛИТЕРАТУРА

1. Turner М. J., Clough R. W., Martin Н. С, Торр L. J., Stiffness and Deflection Analysis of Complex Structures, /. Aero. Set., 23, 805-823 (1956).

2. Clough R. W., The Finite Element in Plane Strese Analysis, Proc. 2nd ASCE Conf. on Electronic Computation, Pittsburgh, Pa., Sept. I960.

3. Timoshenko S., Goodier J. N., Theory of Elasticity, 2nd ed., McGraw-Hill, 1951.

4. Лехницкий С. Г., Теория упругости анизотропного тела, ГИТТЛ, М.-Л., 1950..

5. Hearmon R. F. S., An Introduclion to Applied Anisotropic Elasticity, Oxford Univ. Press, 1961.

6. Zienkiewicz 0. C, Cheung Y. K.. Slagg K. G., Stresses in Anisotropic Media with Particular Reference to Problems of Rock Mechanics, J. Strain Analysis, f, 172-182 (1966).

7. Савин Г. Н., Коицеитрация напряжений около отверстий, ГИТТЛ, М. - Л. 1951.

8. Zienkiewicz О. С, Cheung Y. К, Bultress Dams on Complex Rock Foun dations, Water Power, 16, 193 (1964).

9. Zienkiewicz 0. C, Cheung Y. K., Stresses in Buttress Dams, Water Power. 17, 69 (1965).

10. Herrmann L. R., Elasticity Equations for Incompressible, or Nearly Incom pressible Materials by a Varialional Theorem, JAIAA, 3, 1896 (1965); есть русский перевод: Геррманн, Вариационный принцип для уравнений упругости несжимаемых и почти несжимаемых материалов. Ракетная техника и космонавтика, 3, № 10, стр. 139-144 (1965).

ОСЕСИММЕТРИЧНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ

5.1. Введение

Исследование распределения напряжений в телах вращения (осесимметричных телах) при осесимметричном нагружении представляет большой практический интерес. Поскольку эти задачи тоже двумерные [I, 2], с математической точки зрения они аналогичны задачам о плоском напряженном и плоском деформированном состояниях. Вследствие симметрии деформированное, а следовательно, н напряженное состояния в любом сеченни по оси симметрии тела полностью определяются двумя компонентами перемещений. Такое сечение показано на фиг. 5.1. Если г и 2 -радиальная и осевая, координаты точки, а и о - соответствующие перемещения, легко заметить, что перемещения внутри показанного на рисунке треугольного элемента ijm могут быть описаны с помощью тех же самых функций перемещения, которые использовались в гл. 4.

Соответствующий рассматриваемому элементу объем, по которому должны браться все интегралы, представляет собой тело вращения, показанное на фиг. 5.1.

Как и прежде, треугольный элемент рассматривается главным образом с иллюстративной целью, хотя все основные выводы имеют общий характер.

Для плоской задачи было показано, что в выражение для внутренней работы входят только три компоненты деформации в координатной плоскости, а компоненты напряжения, нормальные к координатной плоскости, не дают вклада в энергию, ибо равны нулю либо напряжения, либо соответствующие деформации.

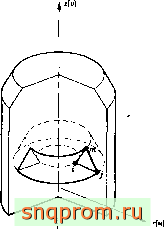
Фиг. 5.1. Элемент осесимметричного тела.

В осесимметричном случае любое радиальное перемещение вызывает деформацию в окружном направлении, и, так как напряжения в этом направлении не равны нулю, в рассмотрение должны быть введены четвертая компонента деформации и соответствующее напряжение. В этом состоит отличительная особенность осесимметричного случая.

Читателю может показаться, что математические выкладки этой главы несколько сложнее использованных в предыдущей, но, по существу, они тоже основываются на общих соображениях, изложенных в гл. 2.

5.2. Характеристики элемента

5.2.1. Функция перемещений

Используя треугольный элемент (фиг. 5.1) с узлами i, j, т, пронумерованными против часовой стрелки, определим узловое перемещение через две его компоненты

а перемещения элемента - вектором

(5.1)

(5.2)

Очевидно, что, как и в подразд. 4.2.1, для однозначного определения перемещений внутри элемента можно использовать линейный полином. Поскольку в этом случае алгебраические выкладки идентичны проделанным в гл. 4, мы не будем их повторять.

Поле перемещений снова определяется соотнощением (4.7)

{n-{l} = UN<,in /Л/;] {6Г.

где

и т. д.,

(5.3)

а / - единичная матрица размерности 2 X 2. В этих соотношениях

Ь(=г/-2 = 2, , (5.4)

f 1 - та if ~ /

остальные коэффициенты получаются циклической перестановкой индексов. Величина Д, как и раньше, представляет собой площадь треугольника.

5.2.2. Деформация (полная)

Как уже упоминалось, в осесимметричном случае необходимо рассматривать четыре компоненты деформации. Это фактически все компоненты, которые могут быть отличны от нуля при осесимметричной деформации. Они и соответствующие им напряжения схематически изображены на фиг. 5.2.

Ггг{т„)

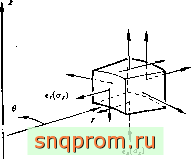
Фиг. 5.2. Деформации и напряжения, определяемые при расчете осеснмметрич-

ных тел.

Все рассматриваемые компоненты вектора деформации можно выразить через перемещения с помощью приведенного ниже соотношения. Использованные выражения очевидны, и они здесь выводиться не будут. Читатель, интересующийся подробным выводом, может обратиться к любому учебнику по теории упругости [3]. Таким образом, имеем

89 f

dv dz ди дг

и

г

(5.5)

1 2 3 [ 4 ] 5 6 7 ... 27