Главная страница сайта  Российские промышленные издания (узловые агрегаты) 

1 2 [ 3 ] 4 5 6 ... 27

подход является единственно возможным. Например, в первых работах по строительной механике строились чисто физические модели, и, хотя приходилось делать некоторые математические оговорки, касающиеся обоснования и сходимости использованных методов, зачастую получались неплохие инженерные решении.

Существуют и другие возможности, позволяющие математически получить основные соотношении метода конечных элементов непосредственно из дифференциальных уравнений задачи. Они будут здесь кратко описаны. Возможные преимущества таких методов состоят в том, что:

а) исчезает необходимость искать функциональный эквивалент известным дифференциальным уравнениям;

б) эти методы могут быть распространены на задачи, для которых функционал либо вообще не существует, либо прка еще не получен [10].

Рассмотрим задачу приближенного решения системы дифференциальных уравнений, которым должна удовлетворять неизвестная функция {ф} в области V. Запишем основное уравнение в виде

Л(Ш) = 0, (3.17)

а граничное условие на границе S как

С({}) = 0. (3.18)

Если пробная функция, удовлетворяющая граничным условиям, записана в общей форме

{ф}а=[тт. (3.19)

где, как и прежде, [N] является функцией координат, а {Ф} - система п параметров, то в общем случае

А{Ш = ЯФ(- (3.20)

Наилучшим решением будет то, которое дает во всех точках области V наименьшую невязку R [1].

Очевидно, это решение можно получить, использовав то обстоятельство, что если невязка R тождественно равна нулю всюду в области, то

\WRdV=Q, (3.21)

где IP-любая функция координат. Если число неизвестных параметров {Ф} равно п, то, выбрав п линейно независимых функций Wi, запишем соответствующую систему уравнений

{WiRdV =\WiA(lN]{(I>})dV = 0, (3.22)

Из которой может быть найдена функция {Ф}. Этот процесс называется методом взвешенных невязок, а Wi - весовой функцией. Выбор различных весовых функций приводит к различным классическим методам.

Коллокация в точке. В этом случае полагается, что Wi=l в некоторой точке i и равна нулю во всех остальных. При этом фактически основное дифференциальное уравнение удовлетворяется в п отдельных точках.

Коллокация в подобласти. В этом методе считается, что Wi= I в некоторой подобласти и Wi - O в остальной части области. Это эквивалентно тому, что интеграл обращается в нуль в некоторых подобластих, число которых достаточно для того, чтобы получить необходимое число уравнений.

Метод Галеркина. В этом случае №'< - Ni, т. е, в качестве весовой функции выбирается функция формы, с помощью которой аппроксимируется решение. Этот метод обычно приводит к наилучшим результатам.

При использовании в любом из упомянутых методов соотношения (3.19), определяющего принятую аппроксимацию, можно выявить основные особенности метода конечных элементов.

Во-первых, результирующая система уравнений будет иметь ленточный вид, так как влияние каждого параметра распространяется только на элементы, примыкающие к рассматриваемой узловой точке.

Во-вторых (в предположении, что, как и ранее, границы между элементами не дают, никакого вклада), интегралы вы-чйс;1яются для каждого элемента независимо, а затем полученные результаты суммируются.

Очевидно, Что правила получения коэффициентов для ансамбли будут такими же, как и в задачах строительной механики, если оператор А линеен [см. уравнение (1.13)].

Здесь следует отметить один недостаток метода взвешенных невязок, В STOM методе дифференциальный оператор А содержит производные более высоких порядков, чем вариационный функционал Х- Таким образом, чтобы избежать вкладов от межэлементных зон (см. разд. 3.2), необходимо обеспечить выполнение условий непрерывности функции формы более высокого порядка. Это обстоятельство имеет важное значение, так как оно сильно ограничивает выбор функции формы и тем самым может вызвать непреодолимые трудности').

) Ниже будет показано, как сужается выбор функций, обеспечивающих непрерывность переменных, если дополнительно задается условие непрерывности угла наклона. В большинстве случаев можно подобрать функцию, обеспечивающую непрерывность только вторых производных.

Эту трудность иногда можно обойти, преобразовывая интегралы в выражении (3.22) с помощью интегрирования по частям (или преобразования Грина - Стокса). Если это преобразование удается выполнить в общем виде и если в результате порядок производных, входящих в полученные интегралы, понижается, то условиям непрерывности должны удовлетворять только эти производные.

Ранее полагалось, что выбранная аппроксимация неизвестной функции [соотношение (3.19)] автоматически удовлетворяет краевым условиям. Однако удобнее записывать уравнения в общей форме, требуя выполнения краевых условий на заключительной стадии, подобно тому, как, например, в строительной механике заданные перемещения и граничные нагрузки учитываются после составления матрицы жесткости ансамбля.

3.5. Пример. Уравнение Пуассона

Для пояснения основных идей, изложенных в предыдущих разделах, рассмотрим чисто математическую задачу решения уравнения в частных производных

(3.23)

в некоторой области V при заданных значениях функции ф = фь на границе (фиг. 3.2, а).

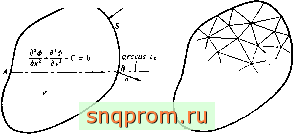
Фиг. 3,2. Метод взвешенных невязок.

Можно показать, что решение этой задачи эквивалентно нахождению функции ф, удовлетворяющей краевым условиям и минимизирующей функционал

Для приближенного решения этого уравнения разобьем область на элементы (фиг. 3.2,6), для каждого из которых

h l = [ivl{r-

(3.25)

где f} -набор параметров, представляющих собой в данном случае значения функции ф в узловых точках элемента.

3.5.1. Минимизация функционала

Равенство (3.4) выполняется, если матрицу [N\ определить так, что функция ф непрерывна между элементами, и, таким образом, мы можем ограничиться рассмотрением типичного элемента.

Подставляя (3.25) в (3.24) и интегрируя по площади элемента, получаем

-))\.дх дф,\дх) ду дф1 \ду) дФГ'У

=SU(

ДЛГ, дМ

дЩ дх

.( дМ,

или

где

дМ, dNi dNi dNj

дх дх

- +

ду ду

)dxdy.

F,=:-\\CNidxdy.

(3.26) (3.27) (3.28)

При заданных форме элемента и функциях формы все эти величины могут быть вычислены и система уравнении для ансамбля будет определяться соотношениями (3.7) -(3.9).

Задача будет полностью сформулирована после учета граничных условий, а ее решение находится из решения системы линейных уравнений,

Глаеа 3

3.5.2. Метод взвешенных невязок

С помощью уравнений (3.22) и (3.23) можно получить типичное уравнение:

И^[1 + 13-+Ф* = 0 (3.29)

в котором функция ф определяется соотношением (3.25). От подынтегральной функции требуется непрерывный переход по границам между элементами с тем, чтобы второй дифференциал был ограниченным. Если мы хотим избежать этого ограничения, можно использовать интегрирование по частям. Так, например.

(3.30)

дх дх

(3.31)

Первый интеграл не содержит вкладов от границ между элементами, если функция ф непрерывна. Теперь необходимо наложить ограничение на весовую функцию W,-. Она должна быть непрерывной, поэтому метод коллокаций в точке или подобласти неприменим. Однако можно использовать метод Га- леркина или любой другой метод, в котором функция Wj непрерывна.

Для Примера используем метод Галеркина, в котором функция веса

Wi = iV,. (3.32)

Используя соотношение (3.25), вклад каждого элемента в интеграл (3.31) можно записать в виде

t кЬФ, + (Fi) -\Ni{-l+ ly)dS=0. (3.33)

В соотношении (3.33) выражения для kb и Ft, по-видимому, не случайно идентичны соответствующим выражениям (3.27) и (3.28), полученным вариационным методом. После суммирования вкладов всех элементов полу1им систему уравнений, аналогичную прежней, за исключением того, что добавляется поверхностный интеграл. Ясно, что этот интеграл не дает вклада в уравнения для внутренних точек (т. е. когда точка i не лежит на границе). Если же точка i лежит на границе, где заданы значения фь, то становится не ясно, как вычислять эгог интеграл; учет же краевых условий делает задачу разрешимой-

Для рассмотренного примера при использовании метода взвешенных иевязок и вариационного метода [11] получаются Одинаковые результаты. Однако если бы использовались другие весовые функции, то совпадения можно было бы и не получить. Тот факт, что прямой метод решения, не требующий знания вариационного исчисления, приводит к тем же самым окончательным результатам, может быть сам по себе интересен читателям и указывает на возможность выбора различных методов решения.

Кроме того, интересно отметить, что поверхностный интеграл в (3.31) имеет определенный физический смысл. Фактически он представляет собой взвешенный интеграл от потока дф1дп через границу, так как

,)dS==\WidS. (3.34)

Иногда На границе бывают известны не значения функции фь, а значения дф!дп. ,В таких случаях правильное решение мог бы дать прямой метод Галеркина, но при этом функционал должен быть модифицирован введением некоторых граничных величин (как это будет сделано в гл. 15).

3.6. Следующий пример. Уравнения вязкого течения

Оператор основного дифференциального уравнения (3.17) может зависеть не только от одной переменной. Можно также рассмотреть систему дифференциальных уравнений. Рассмотрим, например, уравнения, описывающие плоское установившееся течение вязкой несжимаемой жидкости без учета инерционных членов. Неизвестные - давление р и компоненты скорости к и у в направлениях х и у - связаны между собой двумя уравнениями равновесия (уравнения Стокса, полученные

из более общего уравнения Навье - Стокса) [12]: г Р J. Г-и -М п

Y-P j- Г J- о

(3.35)

где X и У -объемные силы на единицу объема жидкости. Уравнение неразрывности дает третье соотношение между этими тремя величинами

л./ я

(3.36)

дх ду

Запишем выражения для р, и, v через узловые значения:

p = [N]{p). u==[N][u}, v = [N]{v), (3.37)

где [N] - функции , формы, обеспечивающие только непрерывность переменных. Используя метод Галеркина, можно записать для точки i систему трех уравнений. Первое нз них и.меет вид

Интегрируя по частям два последних члена в соответствии с соотношением (3.30) и выполняя некоторые преобразования, получаем

dS = 0. (3.39)

После подстановки выражений (3.37) в первое слагаемое имеем

(3.40)

Второе уравнение имеет аналогичный вид н получается из предыдущего путем замены х п и па у к v соответственно. Последнее уравнение, получающееся нз уравнения неразрывности

(3.36), имеет вид

Группируя все переменные, относящиеся к рассматриваемой точке, в виде

получаем уравнение ансамбля в стандартной форме: [К]{Ф} + {Р}==0,

где, опять выделяя вклады каждого элемента, имеем дN дМ,

(3.42)

(3.43)

dN, dNf

aiVj aiv, aJV( алг,

дх дх If ду i dfi

a.v,

(3.44)

Поверхностный интеграл в (3.39) исчезает на той части границы, где задано и, ибо в этом случае Ni = 0. Там, где задано ди/дп, он дает дополнительный член в вектор {F} в уравнении (3.43). Таким образом,

/ ди

I Y\dV+[N,u-

о)

дп ду дп

О

(3.45)

В приведенных уравнениях поверхностный интеграл берется только по внешним границам, на которых заданы duldn или dv/dn. Если же на границе заданы величины и и у, то в граничных точках уравнения не составляются.

Задача о течении жидкости в более простой постановке рассматривалась Докторсом [13].

При другом подходе к решению задачи вводится понятие функции тока. Если положить, что

v = , (3.46)

ТО уравнение неразрывности (3.36) тождественно удовлетворяется и остаются два уравнения

(3.47)

Дифференцируя первое уравнение по у, а второе по д; и вычитая одно из другого, исключаем р, в результате чего остается только одно уравнение

Это уравнение можно решить описанным выше приближенным методом. Читатель может проделать это в качестве упражнения. При решении матрица жесткости получится симметричной и основные соотношения, по существу, будут идентичны соотношениям, рассматриваемым в главе, посвященной изгибу пластин. Однако в этом случае функция формы должна удовлетворять условию неразрывности первых производных между элементами, так как в интегралы будут входить производные второго порядка. Осесимметричные задачи такого рода рассматривались в работе [14].

Примеры были приведены для того, чтобы проиллюстриро--вать общность метода. Однако рассмотренная здесь задача представляет значительный практический интерес, так как в настоящее время большое внимание уделяется разработке методов решения уравнений Навье -Стокса. С целью линеаризации уравнений (3.35) были опущены динамические члены

ду дх ду-

Их можно было и оставить, но тогда уравнение (3.43) получилось бы нелинейным, причем матрица {к\ зависела бы от скоростей. Решение таких уравнений слишком сложно, чтобы его подробно рассматривать здесь, однако можно использовать обобщения рассмотренных в гл. 18 методов решения нелинейных задач.

3.7. Заключительные замечания

В этой главе понятие конечных элементов используется для приближенного решения вариационных задач и рассматривается возможность непосредственного приближенного решения дифференциальных уравнений. Области применения обоих подходов еще недостаточно изучены. Некоторые общие идеи, изложенные в этой главе, рассматривались Оденом [15].

ЛИТЕРАТУРА

1. Crandall S. Н., Engineering Analysis, McGraw-Hill, 1956.

2. Washizu К., Variational Methods in Elasticity and Plasticity, Pergamon Press, 1968.

3. Weinstock R., Calculus of Variations, McGraw-Hill, 1952.

4 Berg P. N, Calculus of Variations, Ch. 16 in; Handbook of Engineering Mechanics, Flugge W., ed., McGraw-Hill, 1962.

5 Southwell R. V., Relaxation Methods in Theoretics Physics, Oxford Univ. Press, 1946.

6. Forsythe G. E., Wasow W. R., Finite Difference Methods for Partial Differential Equations, Wiley, I960; есть русский перевод: Базов В., Форсайт Дж., Разностные методы решения дифференциальных уравнений в частных производных, ИЛ, 1963,

7 Pian Т. Н. Н. and Tong P., Basis of Finite Element Methods for Solid Con-tinua. Int. J. Num. Meth. in Eng., 1, 3-28 (1969).

8 Melosh R J. Basis for Derivation of Matrices for the Direct Stiffness Method, JAIAA, 1, 1631-1637 (1963)-, русский перевод: Мелош, Основы получения матриц для прямого метода жесткостей, Ракетная техника и космонавтика, 1, № 7, стр. 169-176 (1963). ...

9, Plan Т Н. Н., Derivation of Element Stiffness Matrices, JAIAA, 2, 576- 577 (1964); есть русский перевод: Пиан, Получение матриц жесткости элементов. Ракетная техника и космонавтика, 2, № 9, стр. 20 (1964).

10. Stakgold I., Boundary Value Problems in Mathematics and Physics, Mac-millan, N. Y., 1966.

11 Szabo В A., Lee G, C, Derivation of Stiffness Matrices for Problems in Plane Elasticity by Galerkin Method, Int. J. Num. Meth. Eng., 1, 301-310

12 La№rltrom P. A., Chang I, D., Flow at Low Reynolds Numbers, .Ch. 81 in- Handbook of Eng. Mech Flugge W., ed., McGraw-Hill, 1962.

13 Doctors L. J., An Application of the Finite Element Technique for Boundary Value Problems of Potential Flow, Int. I. Num. Meth. Eng., 2, 243- 252 (1970).

14 Atkinson В., Brocklebank M, P., Card C. C, M., Smith J. M Low Reynolds Number Developing Flows, A. I. Ch Eng. J., 15, 548-553 (1969),

15 Oden J T A General Theory of Finite Elements: I, Topological Considera- tions pp. 205-221; II, Applications, pp. 247-260; Int. I. Num. Meth. Eng.,

1 (1969).

4.1. Введение

Решения двумерных задач теории упругости были первыми удачными примерами применения метода конечных элементов [1, 2]. В гл. 2, где были получены основные соотношения метода, такие задачи уже рассматривались для иллюстрации его основ. Эти основные соотношения [(2.1) - (2.3), (2.9), (2.10) и (2.16)] для удобства собраны в приложении II.

В настоящей главе будут более подробно рассмотрены и проиллюстрированы на примерах, имеющих практическое значение, основные зависимости для указанных задач. В дальнейшем мы будем придерживаться именно такого подхода к изложению материала.

Подробно рассмотрен только простейший треугольный элемент, хотя аналогичным образом можно получить основные соотношения и для более сложных элементов, которые описываются в последующих главах.

Читатель, мало знакомый с основными понятиями теории упругости, может найти их в элементарных курсах по этому предмету, в частности в книге Тимошенко и Гудьера [3], обозначения которой будут здесь широко использоваться.

В обеих задачах - о плоском напряженном и плоском деформированном состояниях -поле перемещений однозначно определяется перемещениями и и о в направлениях осей хну прямоугольной системы координат. В обоих случаях рассматриваются только по три компоненты напряжения и деформации в плоскости X, у. В случае плоского напряженного состояния все остальные компоненты напряжения равны нулю по определению и, следовательно, не совершают внутренней работы. В случае плоской деформации напряжение в направлении, перпендикулярном плоскости X, у, не равно нулю. Но поскольку в этом направлении деформация равна нулю по определению, это напряжение также не дает вклада во внутреннюю работу. При желании его можно определить через значения главных компонент напряжения.

4.2. Характеристики элементов

4.2.1. Функции перемещений

На фиг 4 1 показан типичный треугольный элемент с узлами t, i, т, пронумерованными против часовой стрелки. Пере-мещениякаждого узла имеют две компоненты

Ivi)

(4.1)

а шесть компонент перемещений элемента образуют вектор

(4.2)

Перемещения внутри элемента должны однозначно опреде-лятьсятими шестью величинами. Ясно, что простейшим пред-

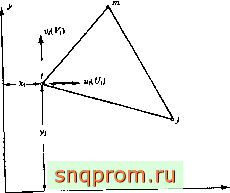
Фиг 4 I Элемент сплошной среды для расчета плоского напряженного или * плоского деформированного состояния.

ставлением являются линейные полиномы u - Oi + aiX + ay, v = ai + aiX-\-a.

(4.3)

Зняцения шести постоянных г легко найти из двух систем, состоящих Г трех уравнений, которые получаются в результате подстаиов^ки в'(4.3) узловых координат и приравнивания

ПЛОСКОЕ НАПРЯЖЕННОЕ

И ПЛОСКОЕ ДЕФОРМИРОВАННОЕ

СОСТОЯНИЯ

перемещений соответствующим перемещениям узловых точек. Записав, например,

= + ал + азУ1, u, = ai + a2Xi + a3yf, (4.4)

выразим а аг, Оз через величины узловых перемещений щ, щ. Urn и окончательно получим

где

+ (а„ + Ь„х + с„у)и„}, (4.5а) (4.56)

Ь1 = У!-Ут = У1т, <!i-Xm - Xj = Xmj;

остальные коэффициенты получаются циклической перестановкой индексов (, /, т, а величина 2Д определяется соотнощением

1 Xi yi

2A = det 1 Xj у,

1 x г/

= 2 (площадь треугольника Цт). (4.бв)

Аналогично можно представить перемещение о в вертикальном направлении;

о = {(а, + btx + ay) vi + (а, -f bjX.+ С/у) v, +

+ (a + b,nx + cy)v}. (4.6)

Хотя на данном этапе в этом нет особой необходимости,

можно записать соотнощеиия (4.5а) и (4.6) в стандартной форме (2.1):

= [N] {бУ = [Ши /Г/, {б} (4.7)

где 7 -единичная матрица размерности 2X2, а Ni = ---- и Т. д.

(4.8)

Примечание: если за начало координат принять центр тяжести элемента, то

Xi + x + x, = yi-\-y -\-y, = Q и а, = -з- = ау = а„.

Выбранная функция перемещений автоматически гарантирует непрерывность перемещений между смежными элементами, так как вдоль любой стороны треугольника они изменяются линейно, и, следовательно, из равенства перемещений в узлах следует их равенство по всей границе.

4.2.2. Деформация (полная)

Полную деформацию в любой точке внутри элемента можно охарактеризовать тремя составляющими, которые дают вклад во внутреннюю работу:

{е} =

ди дх до Зу ди j до

(4.9)

ду дх

Используя равенства (4.7) или (4.5а) и (4.6), имеем

{е} =

дМ] дх

О

О

dtf, ~дГ

О

ду ду dNi dNi dNi dNj ду дх ду дх

ь, о

2Д

дх О

О

щ

от ьп О

О С/ О с, Cl b,

О

bi о

т (4.10)

что явным образом определяет матрицу [В] из равенства (2.2), Следует заметить, что в этом случае матрица [В] не зависит от координа- точки внутри элемента, и, следовательно, деформации в нем постоянны. Очевидно, что эти функции формы удовлетворяют критерию постоянства деформаций, приведенному в гл. 2.

4.2.3. Начальная деформация (температурная деформация)

Начальные деформации, т. е. деформации, не зависящие от напряжений, могут возникать по разным причинам. Усадка, рост кристаллов или чаще всего колебания температуры будут

(4.11)

приводить в общем случае к начальным деформациям, характеризуемым вектором

Хотя величина этой начальной деформации, вообще говоря, может зависеть от координат точки внутри элемента, обычно

Фиг. 4.2. Элемент для расчета слоистого (трансверсально-изотропного) материала.

она считается постоянной и равной некоторому среднему по элементу значению. Это согласуется с условием постоянства деформаций, которому отвечает принятая функция перемещений.

Таким образом, в случае плоского напряженного состояния изотропного материала для нагретого до температуры 9* элемента при коэффициенте линейного расщирения а будем иметь

{ео} = ае=. (4.12)

поскольку при тепловом расширении деформации сдвига отсутствуют.

Сложнее случай плоской деформации. Предположение о плоской деформации означает, что при тепловом расширении возникают напряжения в плоскости, перпендикулярной к плоскости X, у, даже если отсутствуют остальные компоненты напряжения.

Следовательно, величина начальной деформации будет зависеть от упругих постоянных.

Можно показать, что в этом случае

{eo} = (l + v)ae. (4.13)

где v - коэффициент Пуассона.

Особого рассмотрения требуют анизотропные материалы, для которых коэффициенты линейного расширения могут быть различными в разных направлениях. Пусть х' и у' на фиг. 4.2 соответствуют главным направлениям материала. Начальная температурная деформация для случая плоского напряженного состояния в этих координатах будет

{8о} = е^о = а2е'. (4.14)

где 1 и 2 - коэффициенты линейного расширения в направлениях х' и у' соответственно.

Чтобы получить компоненты деформаций в координатах х и у, необходимо использовать соответствующую матрицу [Г] преобразования деформаций:

{8о} = тЧео}. (4.15)

Легко проверить, что

cosp sinp ~2sinpcosf

sinp cosp 2 sin p cos p

l sinPcost

~ sin в cost

cos

где p -угол, определенный на фиг. 4.2. Таким образом, {во} легко вычисляется. Следует заметить, что в координатах х, у компоненты деформаций сдвига отличны от нуля.

4.2.4. Матрица упругости

Матрица [D\ входящая в соотношение (2.3), которое в рассматриваемом случае имеет вид

может быть записана в явном виде для любого материала (в это соотношение не включен аддитивный член {оо}).

(4.16)

3 Зак. 013

Плоское напряженное состояние в изотропном материале.

Для плоского напряженного состояния изотропного материала имеем по определению

2(l+v)T

(4.17)

Разрешая эти соотношения относительно напряжений, получаем матрицу [D] в виде

1 V О

[0] = Т^

V 1 О О

О

1 -у 2 J

(4.18)

где -модуль упругости, а v - коэффициент Пуассона.

Плоское деформированное состояние в изотропном материале. В этом случае, кроме трех компонент напряжения, существует нормальное напряжение Ог. Для частного случая изотропного теплового расширения имеем

EE ~ + >

+ oe

(4.19)

Уху

и, кроме того,

Исключая а„ определим три остальные компоненты напряжения. Полагая начальную деформацию в (4.13) равной нулю и сравнивая с соотношением (4.16), получаем матрицу [D] в виде

(l-fv)(l-2v)

1 - v

о

1 о

о о

1-2у 2(l-v)

(4.20)

Анизотропные материалы. Для описания зависимости между напряжениями и деформациями в случае общей анизотропии в трехмерном состоянии необходима 21 независимая упругая постоянная [4, 5].

Для двумерного состояния число независимых постоянных в матрице [D] не превышает шести. Поэтому в самом общем двумерном случае можно написать

ID] =

d-a d23 ЬСимметрично djj

(4.21)

(Необходимость симметрии матрицы [D] следует из теоремы взаимности Максвелла - Бетти и является следствием инва-

Фиг. 4.3. Слоистый (трансверсально-изотропиый) материал. Плоскость слоев параллельна плоскости х, г.

риантности энергии относительно пути достижения заданного деформированного состояния.)

Особый практический интерес представляет слоистый или трансверсально-изотропный материал, в слоях которого существует круговая симметрия свойств. Свойства такого материала характеризуются пятью независимыми упругими постоянными.

Общие соотношения между напряжениями и деформациями в этом случае в обозначениях, введенных Лехницким [4], при направлении оси у (фиг. 4.3), перпендикулярном плоскости слоев, и отсутствии начальных деформаций имеют вид

vjoj,

El

2(1 +vi)

(4.22)

Уху Xy,

У иг (jj уг

Здесь постоянные Е\, vj (Gi - зависимая величина) характеризуют поведение материала в плоскости слоев, а £2. G2, V2 - в перпендикулярном к ним направлении.

В двумерном случае матрица [D] после введения обозначений

п и

- = т

принимает для плоского напряженного состояния вид

(l- v=)

а для плоской деформации \т - Ё2

(l + v,)(l-v,-2 v)

ft(l- v) /tV2(l+Vi) nV2(l+V,) (l-vl)

n nV2

0

0 m(l- v2)J

j(l+v,)(l -v,-2 vg

(4.23)

(4.24)

Если же слои расположены под некоторым углом к оси х, как показано на фиг. 4.2, то для получения матрицы [D] в произвольной системе координат необходимо выполнить преобразование. Обозначая через \D] матрицу, связывающую напряжения и деформации в системе координат х', у', легко показать, что

[D\ = \T][D]\TY, (4.25)

где [Г] - матрица, введенная в (4.15).

Если напряжения {а') и {а} соответствуют деформациям {е'} и {е}, то из условия равенства работ

или

{eYlD] {e} = {e}4D]{e}

после подстановки (4.15) следует равенство (4.25) (см. гл. 1).

4.2.5. Матрица жесткости

Матрица жесткости элемента ijm определяется с помощью общего соотношения (2.10), в соответствии с которым

lk]=\[BV[D]lB]tdxdy, (4.26)

где t - толщина элемента, а интегрирование производится по площади треугольника. Если предположить, что толщина элемента постоянна, что тем ближе к истине, чем меньше размеры элемента, то, поскольку ни одна из матриц не содержит х или у, имеем простое выражение

[k] = lBV[D][B]t (4.27)

где Л -площадь треугольника [введенная соотношением (3.5)]. Такая форма записи позволяет вычислить матрицу с помощьк) ЭВМ. Матрицу [В], определенную соотношением (4.10), можно записать в виде

lB] = \B Bi,BJ, где [В,] = 0 c,2 и т. д. (4.28) Матрица жесткости может быть записана в виде

(4.29)

где подматрицы размерности 2X2 строятся следующим образом:

lkrs] = [в,r[D][в,]t. (4.30)

Такая форма часто бывает удобной для вычислений,

4.2.6. Узловые силы, обусловленные начальной деформацией

Эти силы определиются в явном виде выражением (2.12), которое после интегрирования принимает вид

{f)l=-[bf[d][zo] ит. д.

(4.31)

1 2 [ 3 ] 4 5 6 ... 27