Главная страница сайта  Российские промышленные издания (узловые агрегаты) 

1 ... 24 25 26 [ 27 ]

Симметричные матрицы

В задачах расчета конструкций часто встречаются симметричные матрицы. Если элементы матрицы [А] обозначить через а,- то для симметричной матрицы

ац = а11.

Можно показать, что матрица, обратная симметричной, всегда симметрична.

Разбиение матриц на клетки

Легко убедиться, что матричное произведение [Л][й],

в котором матрицы имеют, например, вид

		fl32			35

[В] =

&3,

&41

6,2 622 632 642 652

МОЖНО получить, разбивая матрицы, как указано пунктиром, на подматрицы, применяя сначала правила умножения матриц так, как будто каждая подматрица является скаляром, и производя дальнейшее умножение обычным образом. Если записать

Ai . Л21

12 А22-

LB2J

[Л] [В] =

то можно показать, что

. Л21В, -Ь Л22В2-

При разбиении матриц на клетки существенно, чтобы строение подматриц обеспечивало существование произведений вида Лпбь т.е. число столбцов матрицы Лц должно быть равно числу строк матрицы Bi и т. д. В этом случае любые действия над матрицами можно производить так, как будто каждая клетка является скаляром. Отметим, что любую матрицу можно умножить на скаляр (число).

(2.1) {n = [Nm = [Nt,N N ,...]

(2.2) {е} = [В1{бГ.

(2.3) {a} = [D]({e}-{eo}) + {ao}.

(2.9) [FY

=[r{6r+{F}; + {F}:. + {f};.

(2.10)+ [kr\\BY[D\[B]dV, + (2.13) {F)l = -\{NY{p}dV.

{F}l - \[BY\D]dV.

{f}:.= +5[Bf{a }dK.

(2.16) {a} = [D\[fl] {6} - [D] {eo} + a .

(2.17) [5Г = 1Д]1В].

ОСНОВНЫЕ СООТНОШЕНИЯ ГЛАВЫ 2

Приложение з

НЕКОТОРЫЕ ФОРМУЛЫ

ИНТЕГРИРОВАНИЯ

ДЛЯ ТРЕУГОЛЬНИКА (ФИГ. 4.1)

Пусть треугольник в плоскости х - у определен тремя точками (1. yi)i Уд и ( т. Ут)< а начало координат находится в центре тяжести, т. е.

Xi + x, + x У1+У1 + Ут г, 3 3

Интегрируя по площади треугольника, получаем

xdxdy=\ydxdy = 0,

1 Xi yt 1 Xi У/

1 X Ут

\xxdy = j(x + x, + xl).

\dxdy=Y

= Д = площадь треугольника,

\y4xdy(y, + y) + yl), xydxdy=- {х,у( + х/у/ + xy).

Приложение 4

НЕКОТОРЫЕ ФОРМУЛЫ ИНТЕГРИРОВАНИЯ ДЛЯ ТЕТРАЭДРА (ФИГ. 6.1)

Пусть тетраэдр определен в системе координат х, у, г, начало которой расположено в центре тяжести, четырьмя точками

{Хг, Уи Zi), {Xj, У;, Zj), (Хт, Ут, 2ш), (Хр, Ур, Zp), ПрИЧеМ

*i + *; + *m + Ус + У1 + Ут + Ур I+l-m+p

Интегрируя по объему тетраэдра, получаем 1 Xi yt Zi

1 X, У; Z, 1 m Ут Z

= 0.

dxdydz =

= V - объем тетраэдра.

При указанной иа фиг. 6.1 нумерации верщин тетраэдра справедливы следующие формулы:

xdxdydz=ydxdydz=zdx dy dz = О, x4xdydz = {xi+xi + xl, + x,), ydxdydz-(y] + y] + yl + yl), z4xdydz = (z] + zi + zl + zl),

у

ху dx dydz = - (xiyt -f Xjy, -f x </ -f Хру^), xz dx dydz= (XiZt + XjZ, -f x 2 -f x,), yz dx dydz = (yiz, + yjZi + yz + у^г^).

При использовании элементов, произвольно ориентированных в пространстве, например при расчете оболочек и т. п., требуется знание и понимание основ векторной алгебры. Кратко изложим некоторые основные понятия.

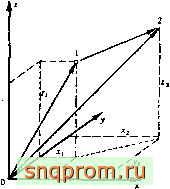
Векторы (с геометрической точки зрения) можно определить их компонентами по направлениям осей х, у, г').Таким образом, вектор .Vol, показанный на фиг. А5.1, можно представить в виде

Voi = i*i + j</i + kz {А5.1)

где i, j, к -единичные векторы в направлениях осей х, у, г. С другой стороны, этот же вектор можно записать как

{loi}=j/! (А5.2)

(как вектор-матрицу), располагая его компоненты в виде столбца.

Сложение и вычитание. При сложении и вычитании векторов производится сложение и вычитание их компонент:

Vo2 - Vo, = Va, = i (X2 - X,) + j ( /2 - J/i) + к (Z2 - 2,). (A5.3)

Этот же результат можно получить, используя правила матричной алгебры, т. е.

У2-уЛ. (А5.4)

Z2 - 2, J

Длина вектора. Из геометрических соображений длина вектора V21 определяется выражением

/2, = V(*2 - х^Г + ({/2 - У1? + (22 - (А5.5)

или в обозначениях матричной алгебры

/i2 = V{iFTiM. (А 5.6)

I) Здесь и дзлее предполагается прямоугольная декартова система координат. - Прим. ред.

Направляющие косинусы. Направляющие косинусц вектора определяются через длины его проекций:

cos о;

и т. д.,

(А5.7)

где 0; - угол между вектором и осью х.

Скалярные произведения. Скалярное произведение двух векторов определяется как произведение длины одного из векторов на длину проекции на линию его действия другого вектора. Та-

Фиг. А5.!. Векторное сложение.

КИМ образом, если у -угол между двумя векторами Л и В, длина которых /д и k, то

А.В = гЛсозу = В. А. B = i&. + j + k6

(А5.8) (А5.9)

то, учитывая, что в соответствии с приведенным определением i.i = j.j=k.k=l.

ролучаем

i-j=j.k = k.i = 0 и т. д.,

(А5.10)

НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ВЕКТОРНОЙ АЛГЕБРЫ

В матричных обозначениях

{4}=а {S} = u,. (А5.11)

X.B=={Ay{B} = {BY{A}. (А5.12)

Векторное произведение. Векторное произведение определяется как вектор, направленный по нормали к плоскости, задаваемой двумя векторами, и равный по величине произведению

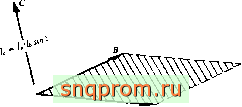
Фиг. А5.2. Умножение векторов (векторное произведение).

длин этих векторов на синус угла между ними. Его направление определяется по правилу правой руки. Так, иа фиг. А5.2 показан вектор

АХВ = С. (А5.13)

Ясно, что

АХВ = -ВХА-. {А5.14)

Отметим, что величина {или длина) вектора С равна площади показанного иа фнг. А5.2 параллелограмма.

Используя представления (А5.9) и замечая, что

iXi = JXj = kXk = 0,

iXJ = k, jXk = l, kXi=J,

(A5.15)

получаем Л X В = det

i j к

a Uy bx by b

(a &, - афу) 1 + {аф, - a,&,) j + {a,by - a,&,) k. (A5.16)

В матричной алгебре нет простого аналога векторному произведению, однако можно использовать для вектора С следующее определение );

{С} = ЛХВ

rayb,-aj}y - J а,6 V - Яг

{А5.17)

афу - Uybj,.

Векторное произведение особенно полезно при построении нормали к поверхности (см. гл. 11).

Элементарные площадь и объем. Если 5 и г) -некоторые криволинейные координаты, то векторы

/ дх \ / дх \

dr)

{А5.18)

определяемые соотнощениями между декартовыми и криволинейными координатами, направлены по касательным к линиям I = const и т) =. const. Поскольку длина векторного произведения d X равна площади элементарного параллелограмма, используя (А5.17), можно записать

дх дх

dl <Jti ду ду

S = det

di d.

(A5.19)

ai дц

Аналогично в криволинейных координатах , t], g трехмерного пространства элементарный объем определяется смещанным произведением

dV=dl-{dfiXdU) = dei

дх dl ду dl dz dl

дх дх

ду дц дг дц

dl dz dl

dld-dt,. (A5.20)

Это соотнощение следует из геометрических соображений. Произведение, стоящее в скобках, по определению представляет собой вектор, длина которого равна площади параллелограмма, построенного на векторах dr\ и d. Скалярное умножение этого вектора на вектор d дает элементарный объем.

) Подробнее см. в книге: Б. Е. Победря, Лекции по тензорному анализу, Изд-во МГУ, {т.- Прим. ред.

Продемонстрируем здесь относительно простой переход от вариационного соотношения к эквивалентному дифференциальному уравнению. Однако обратный процесс гораздо сложнее и его не всегда удается осуществить, поскольку зачастую не удается установить вариационный принцип.

Рассмотрим задачу минимизации функционала

% = \f{x,y, г, ф, ф фу, ф^)йУ + \{яФ+)(18. (А6.1)

V с

Здесь / произвольная функция, фх = дф/дх и т. д., С - часть границы, на которой не заданы значения функции ф. На остальной части границы ф = ф£.

Рассматривая произвольную вариацию неизвестной функции и ее производных, получаем

+ \{д6> + аф6ф)й8. (А6.2) с

Поскольку

соотношение (А6.2) можно переписать в виде

= S й + 1 ()+ )+S +=О-

V с

(А6.3)

Величина 6% приравнена нулю, так как в точке минимума (стационарной точке) вариация обращается в нуль.

Подставляя dV = dxdydz и интегрируя второе слагаемое в первом интеграле по частям [см. формулу (3.25)], получаем

где /х-косинус угла между внешней нормалью к поверхности и осью X. Интегрируя таким же образом остальные слагаемые в (А6.3), окончательно получаем

С

Второй интеграл берется только по части границы С, поскольку на остальной части поверхности S значения ф заданы и поэтому = 0.

Поскольку равенство (А6.4) должно выполняться при произвольной вариации б^, повсюду в области V должно выполняться условие

а на части границы

(А6.56)

Если функция ф удовлетворяет этим двум уравнениям, то она минимизирует функционал %). В случае единственности решения постановки задач с использованием соотношений (А6.1) и (А6.5) эквивалентны. Приведенные дифференциальные уравнения известны как уравнения Эйлера.

Если функционал зависит и от производных функции ф более высокого порядка, то соответствующие этому случаю уравнения Эйлера получаются аналогично. Точно так же можно найти систему дифференциальных уравнений Эйлера для функционала от нескольких независимых функций 0, г|) и т. д. и их производных.

1) При указанных условиях функпионал имеет экстремальное значение. Для того чтобы это экстремальное значение соответствовало минимуму, требуется дополнительное условие. Подробнее см.: Г. Е. Шилор, Математический анализ. - Прим. р^д.

ТЕОРЕМА ЭЙЛЕРА ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ

СОДЕРЖАНИЕ

Предисловие к русскому изданию................5

Предисловие автора ..................... 7

Глава 1. Предварительные сведения: метод жесткостей расчета конструкций и исследование сетей..............11

Глава 2. Конечные элементы упругой среды. Метод перемещений ... 26

Глава 3. Обобщение понятия конечных элементов......... 44

Глава 4. Плоское напряженное и плоское деформированное состояния . 60

Глава 5. Осесимметричное напряженное состояние......... 87

Глава 6. Исследование трехмерного напряженного состояния..... 104

Глава 7. Функции формы элемента. Некоторые семейства этих функций 117

Глава 8. Криволинейные изопараметрические элементы н численное интегрирование ....................143

Глава 9. Некоторые примеры применения изопараметрических элементов при исследовании двумерного и трехмерного напряженных состояний.....................169

Глава 10. Изгиб пластин...................186

Глава II. Оболочки как совокупность плоских элементов ....... 230

Глава 12. Осесимметричные оболочки..............259

Глава 13. Полуаналитнческий метод конечных элементов. Применение

ортогональных функций...............274

Глава 14. Расчет толстостенных оболочек как частный случай исследования трехмерного тела................. 294

Главз 15. Задачи о стационарных полях (теплопроводность, электрический потенциал, течение жидкости и др.).........316

Глава 16. Постановка нестационарных и динамических задач.....344

Глава 17. Динамические задачи. Полуаналитическое исследование. Колебания и собственные значения.............371

Главз 18. Физически нелинейные задачи. Пластичность, ползучесть, задачи

нелинейной теории поля и т. д..............393

Глава 19. Геометрически нелинейные задачи; большие перемещения и неустойчивость конструкций...............438

Глава 20. Вычислительные методы н программы (Ченг и Кинг) , , . . 462

Приложение 1. Матричная алгебра...............526

Приложение 2. Основные соотношения главы 2...........53)

Приложение 3. Некоторые формулы интегрирования для треугольника

(Фи!-- * !).............. .... 532

Приложение 4. Некоторые формулы интегрирования для тетраэдра

(Фис. 6.1)...................

Приложение 5. Некоторые сведения из векторной алгебры......534

Приложение 6. Теорема Эйлера вариационного исчисления . , , , . 538

Ь'ВАЖЛЕМЫЙ ЧИТАТЕЛЬ!

Ваши замечания о содержании кинги, ее оформлении, качестве перевода и другие просим присылать по адресу;

129820, Москва. И-110, ГСП, 1-й Рижский пер., 2. Издательство Мир .

О. ЗЕНКЕВИЧ

МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ В ТЕХНИКЕ

Редактор Л. Якименко Художник А. Смелякоа Художественный редактор В. БНсенгалнев Технический редактор 3. Резннк

Сдано в набор 6ЛП 1975 г. Подписано к печати 8/ГХ 1975 г. Бумага № 2 60X90/,8=17 бум. л. 34 печ. л. Уч.-изд. л. 31.76. Изд. № 20/7928. Цена 2 р. 70 к. Зав. 613

ИЗДАТЕЛЬСТВО МИР Москва, 1-й Рижский пер-., 2

Ордена Трудового Красного Знамени Ленинградская типография- № 2 имени Евгении Соколовой Союзполнграфпрома DpK Государственном комитете Совета Министров СССР по делам издательств, полиграфии н книжной торговли. 198052, Ленинград, Л-62, Измайловский просоект, 29

1 ... 24 25 26 [ 27 ]