Главная страница сайта
Российские промышленные издания (узловые агрегаты)
1 ...
22 23 24 [
25 ]
26 27 С
с с
Учет граничных условий
DO 500 N= ),NB NX= 10..(NDF~ 1)
I = NBC(N)
NROWB = (I - 1).NDF
Проверка каждой степени свободы
DO 490 М = I.NDF
NROWB = NROWB + 1
ICON = NFIX(N)/NX
1F(ICON)450,450,420 420 SK(NR0WB,1)= 1
DO 430 J = 2,\BAND
SK(NROWB,J) = 0
NR = NROWB+ 1 - J
IF(NR)430,430,425 425 SK(NR,J) = 0. 430 CONTINUE
450 ?3i<i=0 *- ° 490 CONTINUE 500 CONTINUE
RETURN
С С С
Программа 20-6
SyBROUTINE SOLVE Спецификация
C0MM0N/C0NTR/TITLE(12),NP,NE,NB,NDF,NCN,NLD,NMAT, NSZF,LI,NT4
COMMON cord(100,2),NOP(200,4},1MAT(200),ORT(25,2),NBC(25), NFIX(25)
1,R1(200),SK(200,40)
IB.AND = 40
Сокращение матрицы
do 300 n = i;ns2f
I = n
do 290 l = 2,nband 1 = 1 + 1 IF(SK(n,l)) 240,290,240 j=gSK(n,l)/SK(n,l)
do 270 K = l,nband J=J+ I
1F(SK(n,K)) 260,270.260
С
С
с с
280 SK(N,L) = C
Сокращение вектора нагрузки для каждого уравнения
RI(I) = R1(I)-C.RI(N) 290 CONTINUE 300 Rl(N) = Rl(N)/SK(N.l)
С С
с
350 360
370 400
Обратный ход
N = NS2F N = N-1 1F(N) 500,500,360 L = N
DO 400 K = 2,NBAND L = L+ 1
IF(SK(N,K)) 370,400,370
R1(N) = R1(N)-SK(N,K)*R1(L)
CONTINUE
GO TO 350
RETURN END
20.6. Вычисление внутренних усилий и вывод результатов
Последним этапом решения обычных линейных задач методом конечных элементов является вычисление внутренних усилий для элемента.
Для каждого элемента необходимо выполнить следующие две операции:
а) сформировать вектор решения в координатах, связанных с рассматриваемым элементом;
б) построить матрицу напряжений для перехода от вектора решения к внутренним усилиям. Эта матрица уже упоминалась в разд. 20.4, где рассматривалась подпрограмма вычисления матрицы жесткости. Она формируется либо путем считывания с внешней памяти, либо путем дополнительного вызова подпрограммы вычисления матрицы жесткости.
Кроме внутренних усилий, часто бывает удобно вычислить некоторые другие силы. Например, в плоских задачах вычисляются значения максимального и минимального напряжений и их направления. В конце работы программы иа печать выводятся необходимые сведения о напряжениях.
При решении более сложных нелинейных задач подпро--грамма вычисления напряжений обычно становится отправной
С С С
точкой для циклического процесса вычисления уточненной матрицы жесткости (зависящей от уровня напряжений) или уточненного вектора нагрузки. Вектор нагрузки обычно строится с^помощью метода начальных напряжений или деформаций (см
Блок-схема и пример подпрограммы. Подпрограмма STRESS выводит на печать перемещения, считает и печатает напряжения в элементах в задачах о плоской деформации.
Обозначения переменных в подпрограмме STRESS
Вектор перемещений Вектор сил элемента Л1атрица обратного хода Вектор перемещений элемента
Максимальное напряжение в Л^-м элементе Минимальное напряжение в М-и элементе Отклонение от вертикали в направлении часовой стрелки линии действия максимального напряжения iV-ro элемента
Примечание. Предложение EQUIVALENCE позволяет использовать массив DIS (2, 100) для вектора решения R1 (200), а массир внутренних сил FORCE (200, 3) - для хранения массива SK.
Программа 20-7
SUBROUTINE STRESS 1
DIMENSION DIS(2,100),FORCE(200,3)
C0MM0N/C0NTR/TITLE(t2),NP,NE,NB,NDF,NCN,NLD.NMAT, NS2F,LI,NT4
COMMON CORD(100,2),NOP(200,4),IMAT(209),ORT(25,2)NBC(25),
NFIX(25) 1,R1(200),SK(200,40) 2,B(3,6), R(8)
EQUIVALENCE (D1S( 1),R1 (1 )),(SK( 1 ),FORCE(I))
DIS (2, 100)* (cm. примечание)
FORCE (200, 3)* (cm. примечание) В (3,6) R (8)*
SMAX
SMIN
Блок-схе.ча подпрограммы STRESS
Вывод перемещений
Начало цикла по злементам
Считывание матрицы напряжений, тлу-ченноО в результате обратного хода
вычисление вектора перемещений элеметА
Вычисление напряжений злемента
Конец иикпа по апементам
Начало иинла по злементам
ычиоление векторов главных напряжений
Печать напряжений
Кшец цикла по злементам
Возврат в основную программу
С С С
С С С
Печать перемещений write(6,i00)
write(b,110) (m,(dis(j,m),j = l.ndf) м ? Ж^( 5>-зно18Р1:асемеытГ)
no f0rmat(i1u,2fi5.4)
Вычисление усилий в элементе
= I.NP)
С С С
с
DO 200 NC= 1,NE
READ(M4) N,((B(I,J),J = 1,6),I = 1.3)
DO 260 1 = l.NCN
M = N0P(N,1)
1F{M.EQ.0) GO TO 260
K = (I- 1).NDF
DO 240 J= l.NDF
IJ = J + К 240 R(U) = D1S(J,M) 260 CONTINUE
IA = K + NDF
DO 300 1 = 1,3
FORCE(N,1) = 0.
DOO 300 J = 1,IA 300 FORCE(N,I) = FORCE(N,I) + B(I,J).R(J) 200 CONTINUE
WR!TEC6,10l)
Вычисление главных напряжений и их направлений
ООО 600 N = l.NE 250 C = (FORCE(N,l)4-FORCE(N,2)U2.
А = SQRT(((F0RCE(N,2) - FOrCE(N,I))/2)..2 + FORCE(N,3)..2) SMAX=C + A SMIN=C-A
IF(F0RCE(N,2).EQ.SMIN)G0 to 700
ANG == 57.29578.ATAN(FOrCE(N,3)/FORCE(N,2)- SMIN))
GO TO 210 700 ANG = 90. 210 CONTINUE
I Печать всех компонент напряжений
400 WRITE(6,I11)
101 FORMAT(I07HO ELEMENT X-STRESS Y.STPP45
Ш {L-fMTT?,0,5F17,Ff2t) - - RETURN
10 12
16 16 17 .18 19 20 21 22 23 24 26 28
29 38 39 40 41 42 43 44 45
54 55
20.7. Пример задачи
На фиг. 20.3 показана простая задача о плоской деформации треугольной области при нагружении вертикальной силой. Для расчета область разбита на 9 элементов с 10 узлами. Треугольник закреплен в точках 1 и 4.
В этой задаче используются следующие подпрограммы:
а) программа
б) подпрограмма
в) подпрограмма
г) подпрограмма
д) подпрограмма
е) подпрограмма
MAIN GDATA LOAD STIFT2 FORMK SOLVE
ж) подпрограмма STRESS
(пр. 20-1),
(пр. -20-2),
(пр. 20 3),
(пр. 20-4),
(пр. 20-5),
(пр. 20-6),
(пр. 29-7).
Ниже приведены инструкции для ввода исходных данных, а также образец данных и печати результатов для показанной на фиг. 20.3 задачи.
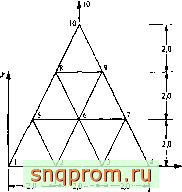
Фнг. 20.3. Плоская деформация треугольной области. -0,96iV=0,2. Эквивалент для плоского напряженного состояния; £=t,0, Л1=0,25.
Инструкции для ввода исходных данных
1. Перфокарта, содержащая информацию о задаче (15)
Кол. 1-5* Номер задачи (nprob) .
2. Перфокарта, содержащая заголивэк (12а6)
Кол. 1-72 Зеголовок, печатаемый при выводе (title)
3. Перфокарта кастройки иа задачу (715) Кол. 1-5* Числ) узловых точек 6-10* Количество элементов 11 - 15* Количество граничных точек 16-£0* Количества случаев нагружения 21-25* К'лнчество степеней свободы = 2 Количество различных материалов О печать исходных данных
26-30 31-35*
1 пропуск печати исходных данных
(NP)
(NE)
(NB)
(NLD)
(NDF)
(NMAT)
4. Перфокарты, содержащие информацию о свойствах материалов (110,2F10.2) (по одной на каждый .материал) Кол. 1 - 10* Номер материала 11-20 Модуль Юнга 21-30 Коэффициент Пуассона
(0RT(N,1)) (0RT(N,2))
5. Перфокарты, содержащие информацию о коордипатах (по одной на каждую узловую точку) (I10,2F10.0) Кол. 1 - 10* Номер узла 11-20 Координата X 21-30 Координата Y
(C0RD(N,1)) (C0RD(N,2))
Перфокарты, содержащие информацию об элементах (615) (по одной иа каждый элгмент)
Кол. 4-5 * Номер элемента (N)
6-10* i (N0P(N,1))
11 - 15* / \ связи между элементами (N0P(N,2))
16-20 т ) (N0P(N,3))
21-25 Не используются (N0P(N,4))
26-30 * Номер материала (IMAT(N))
7. Перфокарты, содержащие информацию р граничных условиях (215) (по одной иа каждое граиичЕгое условие)
Кол. 1-5* Номер граничного узла
6-10* 01 - закрепление в направлении Y
10 - закрепление в направлении X
11 - закрепление в обеих направлениях
8. Перфокарты, содержащие информацию о нагрузке (I10,2F10.2) (по одной иа каждую точку)
Кол. 1-10* Нпмрп v4.:Ta
11-20 21-30
Номер узла Нагрузка по оси X Нагрузка по оси Y
(NBCII)) (NFIX(I))
R(l)
R(2)
Примечание. Перфокарты, содержащие информацию о нагрузке, заканчиваются информацией о нагрузке в поаеднем ya.te незавиЪимо от того, задана в нем нагрузка или иет.
* Означает, что десятичная точка в числе не набивается, остальные числа обязательно должны содержать десятичные точки.
Образец печати исходных данных и результатов Колонки
12 3 4 5 6 7 8
12345678901234567890123456789012345678901234567890123456789012345678901234567890
Расчет треуеольника
9 2 1 0.96
1 2 0.2
| | 2 2. | | |
| | 3 4. | | |
| | 4 6. | | |
| | 6 1. | | |
| | 6 3. | | |
| | 7 6. | | |
| | | | |
| | 9 4. | | |
| | 10 3. | | |
| | | |
| | | |
| | | |
| | | |
| | | Б |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | | |
Расчет треуволькика
10 9 2 1 2
свойства материала
1 96
Топовые точци
2 3 4 Б 6 7 8 9
.ООО 2.000 4 ООО 6,000 1 ООО
3.000
S.000 2.000 4.000
3.000
.ООО ООО .ООО .ООО 2.000 2.000 2.000 4.000 4.000 6.ООО
Элементы
1 2 S
4 7 7 6 6 5
7 9 9 8 9
Граничные условия 1 11
4 11
Расчет треугольника
Случай нагружения 1
Нагрузки
10 .00
Перемещения
10.00
| .0000 | .0000 |
| 1.0941 | 17.7565 |
| -1.0941 | 17.7565 |
| .0000 | .0000 |
| -1.6412 | 15.6785 |
| .0000 | 20.9599 |
| 1.6412 | 15.6785 |
| .8206 | 25.3126 |
| -.8206 | 25.3126 |
| .0000 | 44.4729 |
| Напряже- | Напряже- |
| ние в на- | ние в на- |
| правле- | правле- |
| | | |
1.4902 -.7399 1.4902 .9503 .9503 1.8077 1.8077 -.2949 1.6794
г.1П1 1.4167 3.7727 .5189 .5189 3.9487 3.9487 2.1027 10.0000
Касательное fia-пряжение
3.1136 -.0000 -3.1136 - .6733 .6733 1.3845 -1.3845 .0000 .0000
| | |
мальное | мальное | |
напряже- | напряже- | |
ние | ние | |
5.9477 | -.6847 | 34.935 |
1.4167 | -.7399 | -.ООО |
5.9477 | -.6847 | -34.935 |
1.4417 | .0276 | -53.881 |
1.4417 | .0277 | 53.881 |
4.6283 | 1.1282 | 26.145 |
4.6283 | 1,1281 | -26.145 |
2.1027 | -.29* | .ООО |
10.0000 | 1.6794 | .ООО |
20.8. Графический вывод результатов
Одна из основных проблем, возникающих при практическом использовании метода конечных элементов, связана с огромной информацией, получаемой в результате счета, и с большими затратами времени на обработку выводимых на печать результатов. В значительной степени эту задачу облегчает использование при воспроизведении результатов автоматического самописца.
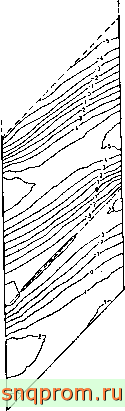
Одним из самых удобных способов представления результатов является построение изостат. Они могут быть построены либо во всей области, либо только в некоторой ее части, представляющей особый интерес. В простейшем случае напряжения в элементе усредняются по узловым значениям. При этом изо-статы вычерчиваются в виде набора прямолинейных в каждом элементе отрезков, согласующихся с этими узловыми значениями. На фиг. 20.4 приведен пример [7]. Недостаточная гладкость кривых вызывает сомнение в правильности решения. Программы, позволяющие вычерчивать гладкие кривые иа основе, данных, полученных в отдельных точках, можно приобрести у предприятий, производящих эти самописцы.
Второй способ использования самописца состоит в вычерчивании для каждого элемента в заданном масштабе векторов главных напряжений в соответствующих направлениях. Такой способ представления напряжений показан на фиг. 20.5.
Большинство применяемых в настоящее время элементов дают скачкообразно меняющиеся от элемента к элементу напряжения, хотя напряжения в двух соседних элементах колеблются относительно истинного. Для сглаживания разрывов напряжений при их описании (и в некоторых случаях для улучшения точности) обычно используются два способа усреднения. Первый заключается в усреднении напряжений по двум смежным элементам. Например, из двух треугольников составляется четырехугольник и в качестве напряжения в некоторой точке четырехугольника принимается среднее по этим двум треугольникам значение. При втором способе усреднения суммируются напряжения всех элементов, соединяющихся в рассматриваемом узле, и сумма делится на число этих элементов. Этот способ обычно дает совершенно гладкую кривую напряжений, достаточно точно описывающую их распределение во всей области, за исключением граничных точек или областей с высоким градиентом напряжений.
Блок-схема. Пример программы. Приведенная ниже программа определения вектора напряжений представляет собой неза-
Сетка С

VuHmugaJlO
Сетка А
Фиг 204 Линии уровней моментов косого моста (из Ргос. Inst. Civ. Eng., 821,
Aug. 1967).
1 тии!


Фиг. 20.5. Автоматическое вычерчивание главных напряжений подпрограммой вычерчивания векторов.
висимую подпрограмму считывания с перфокарт, содержащих напряжения, и вывода на печать в соответствующем масштабе векторов для каждого элемента.
Все такие подпрограммы являются частью набора Calcomp Fortran.Типичная блок-схема приведена на стр. 502.
Программа 20-8
С Подпрограм.ма вычерчивания ве:ктора для Calcomp DIMENSION IBUF(IOOO)
С С С С
Вывод номера барабана и определение места во внешней памяти
LDEV = 1
CALL PLOTS (IBUF,1000,LDEV)
С С С
Считывание масштаба
READ(5,I0) XSHIFT,XSCALE,YSHIFT,YSCALE 10 FORMAT(4FI0.2)
WWTE(6,11) XSHIFT,XSCALE,YSHIFT,YSCALE
Блок-схема программы PROGRAM STVECT
Считывание заданного масштаба
Начало цикла по злементам
Считывание напряжений элемента и координат
Вычерчивание вектора
Обозначение вектора
Конец цикла по элементам
Останов
С С
с с
II F0RMAT(13H1 X SHIFT = ,F10.2/
1 13Н X SCALE = ,F10.2/
2 13H Y SHIFT = ,F10.2/
3 13H Y SCALE = ,F10.2) READ(5,15) PSCALE
15 FORMATiFlO.2) WRITE(6,16) PSCALE
16 FORMAT(13H0PLOT SCALE = ,F10.2,9H UNITS/IN)
Считывание с перфокарт координат и напряжений
100 READ(5,20) N,X,Y,SMAX,SMIN,ANG
WR1TE(6,20) N,X,Y,SMAX,SMIN,ANG 20 FORMAT(I10,2F10.2,3F10.3)
С
с с
с с
Если перфокарта пустая, закончить чертеж
IF(N)210,210,110 Изменение масштаба
НО X = (X-XSHIFT).XSCALE Y = (Y-YSHIFT).YSCALE SMAX = SMAX/PSCALE SMIN = SMIN/PSCALE ANG= ANG/57.3
С С
с
с с с
с с с
с с с
с с с
Вычисление координат концов векторов
R = X + SMAX/2..SIN(ANG) S = Y + SMAX/2..C0S(ANG) р = 2..Х - R Q = 2..Y-S
Вычерчивание отрезков
CALL PL0T(R,S,3) CALL PL0T(P,Q,2) R = X - SMIN.COS(ANG) S = Y + SMIN.SIN(ANG) P = 2..X-R Q = 2..Y-S CALL PL0T(R,S,3) CALL PL0T(P,Q,2)
Печать номера элемента
A = X + 0.2 B = Y + 0.1 FPN = N
CALL NUMBER (A,B,. 14,FPN,0.,0) Переход к следующему элементу
GO ТО 100
Конец чертежа
210 CONTINUE
CALL PLOT (0.,0.,999)
STOP
20.9. Решение задачи о собственных значениях итерационным методом
При исследовании колебаний и устойчивости, а также при расчете методом конечных элементов волноводов и т. д. можно получить систему матричных уравнений вида ИХ = XX, где В - квадратная матрица известных коэффициентов, X - вектор [xi, Х2, XnY, а - скалярная величина, соответствующая собственным частотам, критической нагрузке, частотам среза и т. п. Уравнения вида НХ = XX называются уравнениями собственных значений, и в общем случае они имеют столько решений, т. е. собственных значений и соответствующих собственных векторов, сколько степеней свободы Xi. Примером моГут служить задачи о свободных колебаниях, в которых
Н = К'М. (20.12)
Наибольшее собственное значение можно определить простым итерационным методом;
а) Задать некоторое значение вектора X, которое в дальнейшем называется Xgi. Поскольку собственный вектор характеризует некоторую собственную функцию системы, нам нужны только относительные значения компонент вектора X. Поэтому можно считать, что одна из неизвестных (скажем, Xi) всегда равна единице.
б) Вычислить AXg,. -
в) Произведение AXgi представляет собой вектор, который можно записать в виде A,g2g2, где Xg2 - множитель, такой, что компонента Xi вектора Xg2 опять равна единице, а остальные переменные Х2, х^, .. ., Хп принимают соответствующие значения.
г) Сравнить Xg2 с Xgi пли в общем случае Xg с Х^(г+1). Если они не отличаются (в пределах заданной точности) друг от друга, то полученное множество значений образует собственный вектор, а множитель представляет собой наибольшее собственное значение. В противном случае снова вернуться к пункту а .
Другие собственные значения и соответствующие им собственные векторы определяются методом ловли льва в пустыне в сочетании с итерационным методом. При использовании этого метода матрица Н видоизменяется таким образом, чтобы свести максимальное собственное значение системы к нулю. В результате наибольшим собственным значением становится последующее значение X. После этого процесс итераций повторяется.
Предположим, что на некотором этапе'получены собственное значение Хг и собственный вектор Хг.
Используемую для нахождения X, и Х^ матрицу можно с помощью метода ловли льва видоизменить так, чтобы
избавиться от г-го корня, т. е. сделать Хт равным нулю, не изменяя других собственных значений и собственных векторов. Очевидно, что после этого у видоизмененной матрицы наибольшим собственным значением будет Xr+i- Пусть
Х^М
Zr= г . 20.13)
Можно записать
[Н - XZ - X2Z2 - ... - XZ,] х^ =
- - НХ - XZXf - А.22-г - . - XZjXf - я/, {х\мх я 2 {х1м.х, х\шх ~~ xlmx
(20.14)
Используя свойство ортогональности собственных функций, можно показать, что при г ф s справедливо равенство
xJmXs = 0. (20.15)
Равенство (20.14) можно переписать в виде
[Я-Я,2,-Я222- ... - Я,2,] Jf, = ЯД, - ЯД, = 0Х„ (20.16)
так как XjMXr - скалярная величина и на нее можно сократить.
Из соотношения (20.16) следует, что Х^ все еще остается собственным вектором видоизмененной матрицы, но соответствующее собственное значение Яг равно нулю.
Теперь остается доказать, что другие корни системы не изменяются в процессе ловли льва . Полагая, что Я^ и Х^ - собственное значение и собственный вектор (s > г), можно записать
[Н - XZi - X2Z2 - ... - rZr] х^ =
fix2 - XiZXg - X2Z2X - ... - Xj-ZXg =
X X ,1 -
X{MXj
Следовательно, Я остается корнем видоизменной матрицы.
Свойство ортогональности, использованное в (20.14) и 20.17), доказывается следующим образом. Записываем равенства
К MXs = X,X K~MXr = XrXr.
(20.18) (20.19)
Умножая (20.18) на Х1м\ а (20.19) на Xlhf и выполняя затем операцию транспонирования в последнем уравнении (помня
при этом, что матрицы JiC~ и LcHMMeTpH4Hbi). получаем
xJmk~mx, = хХмх,.
(20.20) (20.21)
Если теперь вычесть (20.21) из (20.20), то в результате получим {Xs-Xr)XjMX, = 0. (20.22)
Так как в общем случае Xj ф %г, то должно выполняться равенство
Х1МХ, = 0. (20.23)
Пример программы
Обозначения переменных в подпрограмме EIGEN
Характеристическаяматрица (К' М или М- К) Матрица масс (или жесткости) Требуемая точность определения собственного вектора
Максимально допустимое число итераций Количество определяемых собственных чисел Квадратный корень из обратной величины собственного значения, используемый вместе с матрицей i? М для определения низших собственных частот
EGG W
TEST
NEIG
С
С С
Программа 20-9
SUBROUTINE EIGEN (EGG,W,NV)
DIMENSION EGG(4,4),X(4),XAUX(4),XUX(4),EAUX(4,4),W(4,4)
EGG - характеристическая матрица W - матрица масс
С
С С
с
READ (5,10) TEST,NIT,NEIQ 10 FORMAT(F10.5,2I10)
TEST - требуемая точность NIT - максимальное число итераций NEIG - количество определяемых собственных чисел
DO 1 II = 1,NEIG DO 66 I = I,NV XUX(I) = 1. 66 X(I)=1.
14 CALL MPRD(EGG,X,XAUX,NV,NV,1) EIQ = XAUX(n DO 571 = 1,NV
Блок-схема программы EIGEN
Считывание основных данных
Начало щГнла Но определяемым собственным аначениям
нет
Выполнение итераций |
| | |
Проверка условия заданной | достижения точности |
| | Нет |
Проверка превышения заданного числа итераций |
| | |
Запись собственнозо значения и собственного вентора |
| | |
Формирование видоизмененной матрицы |
Конец цикла по собственным значениям
Возврат в основную лроерамму
57 X(I) = XAUX(1)/EIG DO 67 1 = 1,NV
IF(ABS((X(I) - XUX(I)/X(I)) - TEST)67,67,82 67 CONTINUE
С С
Достаточно
GO TO 50
Повторение
С С
82 ITS = ITS - 1 IF(ITS)21,21,25
21 WRITE(5,22)
22 FORMAT(26H ITERATION COUNT EXCEEDED) GO TO 50
25 DO 26 I = 1,NV
26 XUX(I) = X(I)
42 FORMAT (4E16.8)
GO TO 14 50 0M = SQRT(1./EIG)
WRITE(5,13) II.OM
WRITE(5,42) (X(IU = 1,4) 13 FORMAT (15,E16.8)
Формирование видоизменений матрицы
CALL TPRD(X,W,XUX,NV,1,NVJ CALL MPRD(XUXAXAUX,1,NV,1) AA = EIG/XAUX(1) DO 68 I = 1,NV 68 XAUX(I) = X(I).AA
CALL MPRD (XAUX,XUX,EAUX,NV,1,NV) DO 110 1 = 1,NV DO 110J=1,NV 110 EGG(I,J) = EGG(I,J) - EAUX(I,J) 1 CONTINUE RETURN END
Программа 20-10
subroutine mprd(d,B,db,l,m,n) dimension d(4,41,B(4,4),db(4,4) DB(l,n) = d(l,m).BiM,n)
x)0 110 J=1,n do 110 1= 1,l DB(i,J) = 0 do 110 k = 1,m
110 db;i,J) = db(i,J) + d(i,k).b(k,J)
return end
Программа 20-11
SUBROUTINE TPRD (D,B,DB,M,L,N) DIMENSION D(4,4),B(4,4),DB(4,4)
; DB(L,N) = (TpaHcnoHHpOBaHHafl D(M,L)).B(M,N)
DO 110 J = 1,N DO 110 I=-1,L DB(I,J)=0 DO 110 K = 1,M 110 DB(I,J) = DB(I.J) + D(K,I)B(K,J) RETURN END
20.10. Заключительные замечания
В этой главе рассмотрен весь процесс реализации метода конечных элементов и приведены образцы программ. Изложенный материал не содержит каких-либо утонченных приемов, которые могли бы оказаться непонятными для начинающих. Напротив, авторы привели достаточно простые, но весьма эффективные рабочие программы, отметив в то же вре^явозможности использования других методов и учета особенностей исследуемой системы'.
Программа решения задач о собственных значениях, приведенная в этой главе, очень проста и не использует свойство симметрии матриц жесткости и масс (или геометрической жесткости). Читателям, интересующимся применением более совершенных методов и возможностями экономии памяти машины, следует обратиться к работе Андерсона [8], посвященной задачам о колебаниях и устойчивости.
ЛИТЕРАТУРА
1. Clough R. W., The Finite Element in Plane Stress Analysis, Proc. 2nd ASCE Conf. on Electronic Computation, Pittsburgh, Pa., Sept. 1960.
2. Irons B. M., Economical Computer Techniques for Numerically Integrated Finite Elements, Ini. S. Num. Meth. Eng., 1, 201-203 (1969).
3. Martin H. C, Introduction to Matrix Methods of Structural Analysis, McGraw-Hill, 1966.
4. Clough R. W., Johnson C. p., A Finite Element Approximation for the Analysis of Thin Shells, Int. J. Solids Struct. 4, 43-60 (1968).
5. King I. P., An Automatic Recording Scheme for Simultaneous Equations Derived from Network Systems (будет опубликовано).
6. Irons В. М., A Frontal Solution Program for Finite Element Analysis, Ini. J. Num. Meth. Eng., 2, 5-32 (1970).
7. Zienkiewicz O. C, King I. P., Discussion on The Analysis of a Four-Span Bridge Using an Electrical Analogue Computers, Proc. Inst. Civ. Eng., 37, 819-820 (1967).
8. Anderson R. G., A Finite Element Eigenvalue Solution System, Ph. D. Thesis, Univ. of Wales, Swansea, 1968. .. --
1 ...
22 23 24 [
25 ]
26 27

