Главная страница сайта
Российские промышленные издания (узловые агрегаты)
1 ...
20 21 22 [
23 ]
24 25 26 27 Для описания мембранной деформации элемента использовалась приведенная в гл. 7 простейшая функция для прямоугольника, а для описания нагибной деформации -несогласованная функция формы для прямоугольника (разд. 10.4 гл. 10).
В работах [11-15] приведены другие примеры использования метода конечных элементов для расчета больших деформаций пластин.
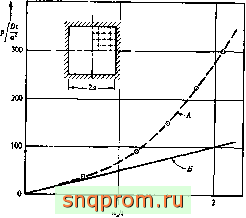
Фиг. 19.2. Прогиб Шс в центре защемленной квадратной пластины при равномерно распределенной нагрузке р [9]. Л -расчет больших прогибов; В-теория малых прогибов.
19.3.5. Бифуркация
В ряде случаев, таких, например, как классическая задача Эйлера, возможна бифуркация равновесия. Рассмотрим пластину, нагруженную лишь в своей плоскости. Поскольку поперечных перемещений w не возникает, теория малых прогибов дает точное решение. Однако даже при нулевых поперечных перемещениях можно определить матрицу начальных напряжений [/Со], хотя [Kl] = 0. Если мембранные напряжения сжимающие, то эта матрица, как правило, будет такой, что из уравнения иэгибной деформации
([кЯ + я[кЯ){б'}=о
(19.32)
можно найти действительные собственные значения. Здесь А,- множитель при мембранных напряжениял, указывающий, при
каком их значении достигается состояние нейтрального равновесия (неустойчивость). При соответствующей этим мембранным напряжениям нагрузке начинается выпучивание и могут появляться поперечные перемещения в отсутствие поперечной нагрузки.
Для постановки этой задачи достаточно записать уравнение изгиба, в которое входят введенная в гл. 10 матрица [ Ко\ и определенная соотношением (19.31) матрица [/Со].
С помощью различных конечных элементов определены точки начала выпучивания для различных задач расчета пластин [16-21]. Некоторые сравнительные результаты для простой задачи расчета квадратной свободно опертой пластины в условиях равномерного сжатия в одном направлении приведены в табл. 19.1. Параметром выпучивания в этом случае является величина
где а -сторона пластины и D - изгибная жесткость.
Таблица 19,1
Значения С для квадратной свободно опертой пластины прв одвоосиом сжатии (точное звачевне С = 4,00 [10])
| | Несогласованные элементы | Согласованные элементы |
| | прямоугольник [17]. 12 степеней свободы | треугольник 119], 9 степеней свободы | прямоугольник [20J, 16 степеней свободы | четырехугольник [21], !6 степеней свободы |
2X2 4X4 8X8 | 3,77 3,93 | 3,22 3,72 3,90 | 4,015 4,001 | 4,029 4,002 |
Все элементы относятся к описанному в гл. 10 типу. Интересно отметить, что при выполнении требования непрерывности углов наклона для параметра выпучивания всегда получаются оценки сверху. При использовании несогласованных элементов в этом случае получаются оценки снизу, хотя в общем случае справедливость этой оценки пока не установлена.
На фиг. 19.3 показана форма выпучивания для пластины более сложной формы [19]. При расчете использовались несогласованные треугольные элементы.
Практическое значение таких задач об устойчивости пластин невелико. Поскольку при наличии поперечных перемещений пластина становится жестче, она может выдерживать дополнительные нагрузки. Такое увеличение жесткости отмечалось в при-
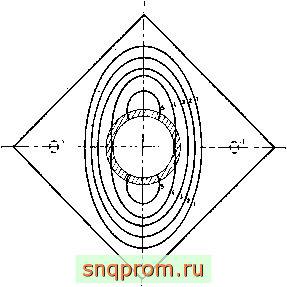
Фиг. 19.3. Форма выпучивания квадратной пластины с защемленными краями и-подкрепленным фланцем центральным отверстием при сдвиге.
Размеры фланца:
мере, иллюстрированном на фиг. 19.2. Таким образом, поведение пластины после выпучивания необходимо исследовать, применяя описанный в предыдущих разделах общий метод изучения больших деформаций [22-24]. Для того чтобы избежать связанных с бифуркацией трудностей, следует задать небольшое возмущение (или поперечную нагрузку).
19.4. Оболочки
Задачи устойчивости для оболочек имеют большее значение, чем для пластин. При исследовании оболочек матрицу тангенциальной жесткости [Кт], как правило, всегда следует определять с учетом действительных перемещений, поскольку, за исключением самых тривиальных случаев, при заданной нагрузке мембранные и изгибные эффекты всегда взаимосвязаны. Одна-
ко, вычисляя матрицу начальной устойчивости [Ко] для упругих напряжений, иногда можно получить полезные результаты относительно коэффициента устойчивости Я. В классических работах по выпучиванию оболочек почти исключительно рассматривается именно такая начальная устойчивость. Однако истинная критическая нагрузка может быть значительно ниже нагрузки, соответствующей начальной устойчивости. Поэтому важно выявить, хотя бы приближенно, влияние деформаций.
Если предполагается, что оболочки состоят из плоских элементов пластин, то к матрице тангенциальной жесткости пластины можно применить описанные в гл. И преобразования [25, 26]. При использовании криволинейных элементов оболочек следует вернуться к уравнениям теории оболочек и включить в них нелинейные члены [9, 27]. Необходимые подробности читатель может найти в упомянутых работах.
Важно опять подчеркнуть, что расчеты начальной неустойчивости имеют смысл только в частных случаях и что они часто дают сильно завышенные значения критических нагрузок. Для
I0SO 540
| | Лин реш | 9йное / вние / | ✓ | |
| | | | | |
| | \50,Всм^ | | |
0.51
1,ог 1,5г
10 Wc, см
2.03
Фиг. 19.4. Прогибы в центре цилиндрической оболочки. Все края защемлены.
=0,32 см. v=0,3, £=3 10 Н/м',
получения правильных результатов необходимо решать нелинейные задачи. Существенное размягчение оболочки под нагрузкой видно иа примере, взятом из работы [9] и иллюстрированном на фиг. 19.4. На фиг. 19.5 показано, что перемещения нагруженной
Г
IE?. 77
217,5
87,0
43,5
0,25 0.51 0.76 т Прогиб в иентре, см
1.27
Фиг. 19.5. Расчет больших деформаций арки методом начальной устойчивости н приращений.
I -решение методом начальной устойчивости; -решение методом конечных элементов [7. Л> 1,21 см. /=0,00229 см<, £=6,74 10 Щм .
арки неограниченно возрастают при величине нагрузки, гораздо меньшей определенной по линейной теории устойчивости [6].
Определение истинной критической нагрузки оболочки или другой тонкой конструкции связано с определенными трудностями (уже рассмотренного в гл. 18 вида), поскольку не может быть сходимости перемещений при увеличении нагрузки вблизи предела несущей способности.
Если рассматривается только сосредоточенная нагрузка, то удобно задавать приращения перемещений и вычислять соответствующие реакции. Аргирис [4] с помощью этого метода изучил поведение арки при нрощелкивании.
Пиан и Тонг [28] показали, каким образом этот прием можно просто обобщить на случай системы пропорционально изменяющихся нагрузок.
В работах [29-33] описаны другие методы исследования потери устойчивости.
19.5. Общий случай больших деформаций и перемещений
Использованные в разд. 19.3 нелинейные соотношения (19.5) между деформациями и перемещениями были выведены спецы' ально для этого случая. Аналогично можно вывести соотношения и для оболочек, кроме того, всегда существует возможность получения и других приближенных выражений. Однако можно использовать общее определение деформаций, справедливое как для больших, так и для малых перемеш^ений и деформаций. Такое определение введено Грином и Сеи-Венаном. Оно известно как тензор деформации Грина. В фиксированной декартовой системе координат х, у, z деформации определяются через перемещения м, о, w выражениями [34]
ди ди ,до д^ ,дт дтЛ (9.33)
Гл.- л„ Г л,.
---- WW I
а ~д7
дх \.дх ду дх ду дх ду У
Остальные компоненты получаются в результате соответствующих перестановок.
Если градиенты перемещения малы, то после пренебрежения квадратичными членами получаем обычные линейные выражения для деформации.
Геометрическая интерпретация вышеприведенных определений деформаций в общем случае не очевидна, но следует отметить, что они являются мерами удлинения и искажения углов первоначально ортогонального элемента.
Если деформации по величине малы, то нетрудно показать, что определяет изменение длины единичного отрезка, первоначально параллельного оси х, а у^у характеризует изменение угла между двумя линейными элементами, первоначально параллельными осям X \1 у. Это справедливо даже при движениях, связанных с большими переносом и поворотом первоначальных осей координат.
Далее выводятся нелинейные выражения для матриц [В] и [Кт] в общем случае трехмерного напряженного состояния. Из
этих выражений просто получить одномерные и двумерные формы. Это предоставляется проделать читателю в качестве упражнения. Общие соотношения удобно использовать для задач расчета пластин и оболочек. При этом можно учесть некоторые члены, которыми мы пренебрегали в записанных в предыдущем разделе выражениях для пластин.
19.5.1. Построение матрицы [SJ
Вектор полной трехмерной деформации можно представить через компоненты бесконечно малой и большой деформаций
где
{6 } =
{е} = | {в } -f {в^}. |
| | | |
| | | |
| | дп ду |
| | | |
| | | |
| | | dz 1 |
Угх Уху | | dw , дх + |
(19.34)
dw ду ди
dz dv
(19.35)
столбец, рассмотренный в Гл. 6. Нелинейные члены в соотношении (Ш.ЗЗ) удобно переписать в внде
где
о о о
о о о
Гди
О О
{xY о
ад [ = 4-И] {9}, (19.36)
dv dw
и т; д.,
а [Л] - матрица размерности 6x9.
Читатель легко может убедиться в справедливости записанного выше соотношения и проверить выполнение свойств матриц
[А] и {0}, описанных в подразд. 19.3.2 (примечание иа стр. 447). В этом случае
rf-{et} = {d[A] {9} +jlA]d{0} = [А]d {9}, (19.37)
и так как (9} можно выразить через функцию формы [Щ и узловые параметры (6}, то
{9} = [G]{6} (19.38)
или
d{8}=H][G]d{6}
Ш = [АШ. (19.39)
19.5.2. Построение матрицы [Кт]
Замечая, что
[S]=[Bo] + [5j,
легко построить матрицу, определенную соотношением (19.7):
[K]-=[Ko] + lKi]=\lB]4D][B]dV. (19.40)
Для получения полной матрицы тангенциальных жесткостей необходимо построить матрицу начальных напряжений [КА- В соответствии с (19.8) имеем
[Ka]d{a) = \ d [Bif {а} dV = \ [GV d[Ar {<т} dV. (19.41)
Можно записать
. Симметрично
Oyh -yzh
где /з - единичная матрица размерности 3X3. Подставляя (19.42) в (19.41), получаем
d{9} = [Af] [G]d{6}, (19.42)
[K,] = \[GY[M][G]dV,
(19.43)
где [М] - матрица размерности 9 X 9 из шести компонент напряжения, расставленных, как показано в (19.42). Очевидно, что матрица [Ко] симметрична.
В предыдущих выражениях индекс элемента опущен, хотя все матрицы должны строиться для каждого элемента, а затем суммироваться обычным образом..
В случае необходимости введения непротиворечивых упрощений при исследовании пластин и оболочек полезно начинать с общих выражений. Эти выражения необходимо использовать и при исследовании рассмотренных в гл. 14 толстых оболочек.
Если известна связь между напряжениями и деформациями, то ее можно использовать для исследования больших деформаций. Однако чаще определяют непосредственно энергию деформаций через компоненты деформации и, минимизируя ее, находят обобщенные силы. Некоторые примеры такого подхода к исследованию больших деформаций даны Оденом [35-38], который рассмотрел большие деформации резиновых' мембран и сплошных сред.
19.6. Заключительные замечания
В этой главе сделана попытка подойти ко всем задачам о больших деформациях с одних и тех же позиций. Указаны различные методы решения основной системы нелинейных уравнений, и вполне естественно, что перед читателем может встать вопрос, какой из этих методов предпочтительнее. Если требуется найти лишь одно решение нелинейной задачи о больших деформациях, то в большинстве случаев оказывается, что метод Ньютона сходится довольно быстро. Однако в некоторых случаях экономически выгоднее применять методы, использующие постоянную матрицу.
Если требуется исследовать весь процесс деформирования при нагружении, то, как правило, рассматриваются малые приращения нагрузки и для каждого такого приращения решается задача линейной теории упругости, причем матрица тангенциальных жесткостей вычисляется для начала приращения нагрузки [2, 3]. При использовании этих методов может накапливаться ошибка, и поэтому Бреббиа и Коннор [9] рекомендуют после нескольких приращений уточнять решение методом Ньютона.
Рассмотренные методы можно использовать для решения геометрически нелинейных задач динамики, особенно когда существуют матрицы жесткости, соответствующие начальным напряжениям, и рассматриваемая задача квазилинейна. Андерсеном и др. [19], например, решено много задач о колебаниях предварительно сжатых пластин').
Если можно построить матрицу упругих постоянных для приращений, то совместное рассмотрение физической и геометрической нелинейностей становится особенно простым. Марсал [2]
) В работе [39] исследовались переходные процессы в таких задачах.
решил ряд таких задач о больших пластических деформациях. Интересно отметить, что приемы решения нелинейных задач при физической и геометрической нелинейностях сходны. Это позволяет разработать вычислительные программы решения задач с учетом обоих типов нелинейности.
В заключение следует отметить два обстоятельства. Во-первых, это сравнительно громоздкое построение матрицы начальных напряжений для пластин, хотя в ряде ранее опубликованных работ изложен более простой способ построения. Однако при этом, как нам кажется, удалось достичь общности изложения. Во-вторых, применение используемых в книге матричных обозначений в разделе о больших деформациях потребовало осуществления достаточно сложных преобразований. Некоторых упрощений можно было бы достичь при использовании тензорных обозначений. Кстати, их можно было бы применить по всей книге. Однако избранный нами путь более доступен и понятен.
ЛИТЕРАТУРА
1. Truesdell С. (ed.), Continuum Mectianics IV, Problems of Non-Linear Elasticity, Vol 8, p. 4, Gordon and Beach, 1965.
2. Mar?al P. V., Finite Element Analysis of Combined Problems of Material and Geometric Behaviour, Techn. Rept. 1, ONR, Brown Univ., 1969; Proc. Am. Soc. Mech. Eng. Conf. on Computational Approaches in Applied Mechanics, 133, June 1969.
3. Argyris J. H., Kelsey S., Kamel H., Matrix Methods of Structural Analysis, AGARD-ograph 72, Pergamon Press, 1963.
4. Argyris J. H., Continua and Discontinua, Proc. Conf. Matrix Methods in Structural Mechanics, Air Force Inst, of Techn., Wright Patterson A. F. Base, Ohio, OcL 1965.
5. Nayak G. C, Plasticity and Large Deformation Problems by Finite Element Method, Ph. D. Thesis, Univ. of Wales, Swansea, 1971.
6. Mar?al P. v.. Effect of Initial Displacement on Problem of Large Deflection and Stability, Techn. Rept, ARPA E54, Brown Univ., 1967.
7. Marguerre K., Ober die Anwendung der Energetischen JWethode auf Stabi-litatsprobleme, Hohrb., D. V. L., 252-262, 1938.
8. de Veubeke B. F., The Second Variation test with Algebraic and Differen-tiaLContrasts, Advanced Problems and Methods for Space Flight Optimisation, Pergamon Press, 1969.
9. BrelJbia C, Connor J., Geometrically Non-Linear Finite Element Analysis, Proc. Am. Soc. Civ. Eng., 95, EM2, 463-483 (1969).
10. Timoshenko S. P., Gere J. M., Theory of Elastic Stability, McGraw-НШ, 2nd ed., 1961.
11. Schmit L. A., Bogner F. K., Fox R. L., Finite Deflection Structural Analysis Using Plate and Cylindrical Shell Discrete Elements, Proc. AlAA/ASME 8th Struct, and Stress Dynamic Conference, Palm Springs, California, 197- 211, March 1967; JAIAA, 5, 1525-1527 (1968); есть русский перевод: Шмит, Богнер, Фокс, Расчет конструкций прн конечных прогибах с использованием дискретных элементов пластин н оболочек. Ракетная техника и космонавтика, № 5, стр. 17 (1968).
12. Turner М. J., Dill E. H., Martin H. C, Melosh R. J., Large Deflection of Structures Subjected ot Heating and External Loads, J. о/ Aero. Sciences, 27, 97-106 (1960).
13. Kawai Т., Yoshimura N., Analysis of Large Deflection of Plates by Finite Element Method, Ini J. Num. Meth. Eng., 1, 123-133 (1969).
14. Mallett R. H., Marcal P. V., Finite Element Analysis of Non-Linear Structures, Proc. Am. Soc. Civ. Eng.. 94, S. T. 9, 2081-2105 (1968).
15. Murray D. W-, Wil.son E. L., Finite Element Large Deflection Analysis of Plates, Proc. Am. Soc. Civ.. Eng., 94, EM I, 143-165 (1968).
16. Martin H. C, On the Derivation of Stiffness Matrices for the Analysis of Large Deflection and Stability Problems, Proc. Conf. Matrix Methods in Struct. Mech., Air Force Inst, of Techn., Wright Patterson A. F. Base, Ohio, Oct. 1965
17. Kapur K. K., Hartz B. J., Stability oi Thin Plates Using the Finite Element Method, Proc. Am. .Soc. Civ. Eng., EM2, 177-195 (1966).
18. Gallagher R. H., Padlog J., Discrete Element Approach to Structural Instability Analysis. JAIAA, 1, 1537-1539 (1963); есть русский перевод: Гал.пагер, Падлог, Исс.педование устойчивости конструкций на основе анализа дискретных элементов. Ракетная техника и космонавтика, № 6, стр. 194 (1963).
19. Anderson R. О., Irons В. М., Zienkiewicz О. С, Vibration and Stability of Plates Using Finite Elements, Int. J. Solids Struct., 4, 1031-1055 (1968).
20. Carson W. G., Newton R. E., Plate Buckling Analysis Using a Fully Compatible Finite Element, JAIAA, 8, 527-529 (1969); есть русский перевод: Карсон, Ньютон, Анализ выпучивания пластинки с использованием полиостью совместного конечного элемента. Ракетная техника и космонавтика, № 3, стр. 174 (1969).
21. Kabaila А. Р., de Veubeke В, F., А Quadrilateral Element for Plate Buckling Analysis, Int. J. Num. Meth. in Eng. (в печати).
22. Murray D. W., Wilson E. L., Finite Element Post Buckling Analysis of Thin Elastic Plates, Proc. 2nd Conf. Matrix Meth, in Struct, Mech Wright Patterson Air Force Base, Ohio, 1968.
23. Rockey K. C, Bagchi D. K., Buckling of Plate Girder Webs Under Partial Edge Loadings, Int. J. Mech. Sci., 12, 61-76, (1970).
24. Roberts T. M., Ashwell D. G., Rost-buckling Analysis of Slightly Curved Plates by the Finite Flement Method, RepL 2, Dept. ol Civil and Struct. En-
fineering, Univ. of Wales, Cardiff, 1969. nderson R. G., A Finite Element Eigenvalue Solution System, Ph. D. Thesis, Univ. of Wales, Swansea, 1968.
26. Gallagher R., Gellatly R., Mallett R Padlog J., A Discrete Element Procedure tor Thin Shell Instability Analysis, jAlAA, 5, 138-145 (1967); есть русский перевод: Галлагер, Джеллатли, Падлог, Моллети, Расчет неустой-чиностн тонких оболочек методом дискретных элементов, Ракетная техника и.космонавтика, № 1, стр. 161 (1967).
27. Gallagher R. Н., Yang Н. Т. У., Elastic Instability Predictions for Doubly Curved Shells, Proc. 2nd Conf. Matrix Methods, Air Force Inst, of Techn., Wright Patterson A. F. Base, Ohio, 1968.
.28. Plan T. H. H., Tong P., Variational Formulation of Finite Displacement Analysis, Symp. Int. Un. Th. Appl. Mech. on High Speed Computing of Elastic Structures, Liege, 1970.
29. Martin H. C, Finite Elements and the Analysis of Geometrically Non-Linear Problems, U. S. -Japan Seminar on Matrix Methods in Structural Analysis and Design, Tokyo, 1970.
30. Walker A. C, A Non-Linear Finite Element Analysis of Shallow Circular Arches, Int. J. Solids Struct., 5, 97-107 (1969).
31. Thompson J. M. Т., Walker A. C, A Non-Linear Perturbation Analysis of Discrete Structural Systems, Int. J. Solids Struct., 4, 757-767 (1968).
32. Przemieniecki J. S., Stability Analysis of Complex Structures Using Discrete Element Techniques, Symp. on Struct. Stability and Optimisation, Loughborough Univ., March 1967.
33. Connor J., Morin N., Perturbation Techniques in the Analysis of Geometrically Non-Linear Shells, Symp. Int. Un. Th. Appl. Mech. on High Speed Computing of Elastic Structures, Liege 1970.
34. Fung Y. C, Foundation oi Solid Mechanics, Prentice Hall Int., 1965.
35. Oden J. Т., Finite Plane Strain of Incompressible Elastic Solids by the Finite Element Method, The Aeronautical Quarterly, 19, 254-264 (1967).
36. Oden J. Т., Sato Т., Finite Deformation of Elastic Membranes by the Finite Element Method, Int. J. Solids and Struct. 3, 471-488 (1967),
37. Oden J. Т., Numerical Formulation of Non-Linear Elasticity Problems, Proc. Am. Soc. Civ. Eng., 93, ST3, 235-255 (1967).
38. Oden J. Т., Finite Element Applications in Non-Linear Structural Analysis, Proc, Symp. on Application of Finite Element Methods in Civil Engineering, Am. Soc. Civ. Eng., Vanderbilf Univ., 1969.
39. Stricklin J. A, Non-Linear Dynamic Analysis of Shells of Revolution, Symp. Int. Un. Th. Appl. Mech. on High Speed Computing of Elastic Structures, Liege, 1970.
20.1. Введение
Метод конечных элементов легко программируется для быстродействующих вычислительных машин и достаточно эффективен, поскольку с помощью ЭВМ можно решать большие системы линейных алгебраических уравнений, которые получаются после дискретизации задачи [1].
Для расчета методом конечных элементов разработано большое количество программ. Первоначально они имели узко специальное назначение и часто составлялись на машинном языке. Подмеченное в процессе различных приложений сходство в структуре программ привело к созданию более совершенных и универсальных программ. Одним из первых примеров является программа ASKA), ориентированная на определенный тип машины. Например, в области исследования аэрокосмических проблем особое значение имеет возможность решения множества различных задач; составление универсальной программы для расчета небольшого числа задач малоэффективно.
, Быстрые темпы развития вычислительной техники привели к необходимости создания программы на языке, понятном любой машине. Возможности алгоритмического языка ФОРТРАН обусловили его широкое использование для программирования при решении задач методом конечных элементов.
Программа NASA) представляет собой попытку создания гибкой программы для широких исследований и решения задач Американской аэрокосмической промышленности.
Созданные в Суонси программы FESS (Finite Element Solution Swansea) и FINESSE были больше ориентированы на эффективное решение инженерных задач строительной механики малых и средних размеров, таких, например, как расчет мо,-стов, плотин, ядерных реакторов. При их разработке основное внимание уделено созданию простой системы, которую легко приспособить к любым конкретным задачам.
Важно иметь в виду, что затраченные усилия при программировании должны окупаться эффективностью программы. Чем
>) Составлена под руководством проф. Аргириса (Штутгарт).
Нациоиалыюе управление по аэронавтике и исследованию космического пространства,
меньшую по размеру предстоит создать программу, тем больше внимания следует уделить ее эффективности. При составлении программы решения задач методом конечных элементов важно знать пределы возможностей машины и при необходимости использования специальных приемов переходить к ЭВМ с большим объемом памяти и большим быстродействием. Программирование в машинных кодах, как правило, происходит более медленно, и разработка такой программы обходится дороже.
Программа и приемы программирования, описанные в этой главе, имеют ряд особенностей, присущих программе FESS. Однако многие приемы и тонкости рационального использования памяти, характерные для программы FESS, здесь опущены ради простоты. Тем не менее приведенная программа без каких-либо существенных изменений использовалась для расчета сложных упругопластических задач. И хотя здесь приведен всего лишь простейший вариант программы, с ее помощью успешно исследовались методом собственных функций также задачи устойчивости и теории колебаний.
20.2. Программы, реализирующие метод конечных элементов
Программы, реализующие метод конечных элементов, могут иметь различное назначение. Чаще всего требуется только решение линейных задач в.упругой постановке, однако число степеней свободы может быть различным, от нескольких десятков до нескольких- тысяч. В задачах динамики и устойчивости может потребоваться отыскание собственных значений, а для решения нелинейных задач может оказаться необходимым применение различных итерационных методов.
При решении конкретных задач методом конечных элементов встретятся непреодолимые трудности, если составлять программу для каждого нового класса задач. Поэтому очень важно использовать созданные ранее программы.
Типичная программа, реализующая метод конечных элементов, состоит из ряда общих блоков, которые в различных контекстах могут использоваться по-разному. Такими блоками являются ввод исходных данных, вычисление жесткости элементов, решение уравнений, построение матрицы масс, нахождение собственных значений, вычисление напряжений и вывод на дисплей.
При программировании такие блоки используются как подпрограммы. Для обеспечения взаимозаменяемости входные параметры этих подпрограмм должны быть стандартизированы. Тогда при составлении новой программы в каждом конкретном случае можно просто комбинировать соответствующие подпрограммы, и вся дополнительная работа программиста сведется
ВЫЧИСЛИТЕЛЬНЫЕ МЕТОДЫ И ПРОГРАММЫ (ЧЕНГ И КИНГ)
лишь к введению каких-либо новшеств или дополнений, связанных со спецификой задачи.
В таких системах управляющая программа обычио.представ-ляет собой очень простую программу, которая обращается в соответствующем порядке к различным подпрограммам. Для некоторых классов задач можно создать стандартные управляющие программы и автоматизировать выбор нужных подпрограмм. В больших организациях, имеющих дело с некоторыми определенными типами задач, создание таких стандартных программ может оказаться чрезвычайно полезным. Однако в исследовательских целях, видимо, предпочтительнее более гибкое ручное программирование.
Важно, чтобы сформированные блоки имели достаточное количество документации, позволяющей легко использовать их не только непосредственному составителю, но и другим лицам. Крайне полезным может оказаться включение в соответствующие места комментариев.
Пример управляющей программы. В этой главе приведен пример программы расчета линейной задачи о плоской деформации, не требующей большого объема памяти машины, что позволяет применять ее в малых ЭВМ. Программа написана на языке ФОРТРАН IV н представляет собой очень простой прн-, мер использования отдельных подпрограмм. Однако она вполне пригодна для решения практических задач и легко, может быть использована читателями, знакомыми с ФОРТРАНОМ. В разд. 20.7 описан пример решения с помощ,ью этой программы задачи о плоском напряженном состоянии (с измененными материальными константами). Прн нспользованни подпрограмм в других целях или при применении элементов других типов i!e-обходимо составить соответствующие управляющие программы. Типичная блок-схема управляющей программы приведена на стр. 467.
Заметим, что в этой программе цикл по нагрузкам вводится в целях экономии памяти вычислительной машины, что, однако, приводит к увеличению затрат машинного времени. Тем не менее, когда есть необходимость отдельно исследовать влияние большого числа различных видов нагрузок, как, например, прн расчете мостов, его введение обязательно. Для задач с небольшим разнообразием нагрузок часто бывает предпочтительнее рассматривать их одновременно.
Обозначения переменных общего блока (CONTR) TITLE (12) Массив для заголовка нз 12 символов
П... ...к-----.. -------
NP N6
Число узловых точек Число элементов
NB Число узлов, в которых заданы граничные
условия
NDF Число степенен свободы узла
NCN Максимальное число узлов в элементе
NLD Количество случаев нагружения
NMAT Количество типов материала
NSZF Число уравнеинй в системе
LI Счетчик цнкла по нагрузкам
NT4 Порядковый номер запоминающего устрой-
Основные переменные, помещаемые в область COMMON
CORD (100,2) Массив координат узловых точек NOP (200,4) Массив, содержащий информацию о связи
элементов
IMAT (200) Массив, содержащий информацию О типе
материала элемента ОРТ (25,2) Массив, содержащий характеристики ма-
териала элемента NBC (25) Номера узлов, в которых заданы гранич-
ные условия NFIX (25) Тип граничного условия
R1 (200) Вектор нагрузки
SK (200,40) Прямоугольная матрица для уравнений
Обозначения переменных в программе МАШ
NPROB Количество задач
NPR Счетчик числа задач
С С С С
С С С
программа 20-1
Управляющая программа MAIN , .
COMMON/CONTR/TITLE(12),NP,NE,NB,NDF,NCN,NLD,NMAT,
COMMONCORD(100.2),NOP(200,4),IMAT(200),ORT(25,2),NBC(25),
NFIX(25) 1,R1(200),SK(200,40)
Номер исходной ленты и максимальное число узловых точек
N14 = И
NCN = 3
READ(5,1) NPROB Начало цикла по задачам
С С С
С С С
С С С С
DO 400 NPR = l.NPROB REWIND NT4
Считывание исходных данных по геометрии и свойствам материалов
CALL GDATA NSZF = NP.NDF DO 200L1 = l.NLD
Считывание нагрузки
CALL LOAD 23
Формирование и решение системы алгебраических уравнений
С С С
CALL FORMK CALL SOLVE
Вычисление напряжений
CALL STRESS 200 CONTINUE 400 CONTINUE 1 FORMAT(915) STOP END
32 33 33 36 37
20.3. Ввод исходных данных
Для работы программы, реализующей метод конечных элементов, дополнительно требуются четыре основные системы исходных данных:
а) координаты и характеристики элементов;
б) свойства материала каждого элемента;
в) граничные условия;
г) нагрузки.
Подпрограммы ввода исходных данных могут иметь различную структуру, но в любом случае их основное назначение состоит в формировании массива исходных данных указанных четырех систем, характеризующих задачу. Для работы управляющей программы необходим полный набор исходных данных.
20.3.1. Координаты и характеристики элементов
Используемые координаты - это координаты всех узловых точек (например, координаты х, и j/j узла i в задаче о плоском напряженном состоянии), расположенные в определенном порядке. В большинстве случаев матрицы жесткости ие зависят- от положения начала координат, которое обычно выбирается произвольно.
Блок-схема програ.чмы МАШ
очитывание итрориации о ноличестВе решаемых . oadaif
Начало цикла по аадачам
Выаов подпрограммы ввода исходных данных
Начало цикла по нагруакам
Выгод поЗпрограммы ввода наеруэни
Вызов подпрограммы (рорма-рования матрицы жесткости
Выаов подпрограммы решения системы /равнений
Вывод подпрограммы напряжений
Конец цикла по нагруонам
Конец цикла по аадачам
Останов
14 19 21 22
К характеристикам элементов относятся информация о связи между элементами, содержащая номера всех узлов элемента, а также число, характеризующее свойства материала элемента. Эти характеристики также перечислены последовательно.
20.3.2. Свойства материала
В большинстве приложений свойства материала одинаковы для больших групп элементов. Поэтому удобно присвоить каждому элементу номер, определяющий материал элемента, и ин-фо()мацию о свойствах материала считывать отдельно.
20.3.3. Нагрузки
Для обеспечения максимальной простоты и гибкости программы нагрузки можно задавать в виде одного вектора, который затем непосредственно используется в программе. Во многих случаях, когда число точек, в которых задана нагрузка, составляет лишь небольшой процент от общего числа узлов системы, бывает предпочтительнее считывать только ненулевые значения нагрузки и номера соответствующих узлов. Вектор нагрузки должен быть, конечно, задан нулевым, чтобы его компоненты, соответствующие ненагруженным узлам, были нулевыми.
Однако в тех случаях, когда рассматриваются объемные силы, для формирования вектора нагрузки в зависимости от геометрии системы и свойств материала необходимо иметь специальную подпрограмму. Подпрограммы формирования вектора нагрузки можно также использовать для вычисления значений узловых сил при действии распределенной нагрузки. В результате работы таких подпрограмм получаются векторы нагрузки, идентичные по форме обычным векторам, считываемым с перфокарт.
20.3.4. Граничные условия
Граничные условия могут быть учтены либо при построении элементов, либо путем соответствующего изменения системы алгебраических уравнений непосредственно перед ее решением. Последний подход удобен для элементов простой формы, но становится сложным при использовании элементов высоких порядков или при необычных граничных условиях, как, например, при ограничениях, накладываемых в некотором произвольном направлении. В приведенной в этом разделе подпрограмме граничное условие для узла считывается в виде комбинации цифр О и 1, причем О означает отсутствие ограничений на данную степень свободы, а 1 - наличие ограничений. Таким образом,
01 означает свободу в направлении x и отсутствие перемещений в направлении У;
10 означает отсутствие перемещения в направлении x и свободу в направлении У;
И означает отсутствие перемещений в обоих направлениях.
Примеры подпрограмм. Ниже помещены тексты двух подпрограмм. Подпрограмма GDATA считывает основные исходные данные о геометрии, а подпрограмма LOAD считывает векторы нагрузки. Ни одна из них не может самостоятельно вырабатывать исходные данные. Блок-схемы этих подпрограмм приведены на стр. 470 и 471.
Обозначения переменных в подпрограмме GDATA П Вывод на печать введенных исходных данных
Обозначения переменных в подпрограмме LOAD
R(3) * Массив для временного хранения значений на-
грузки в узле NQ
Программа 20-2 SUBROUTINE GDATA ]
C0MM0N/C0NTR/TITLE(12),NP,NE,NB,NDF,NCN,NLD,NMAT, NSZF,LI,NT4
COMMON CORD(I00,2),NOP(200,4),IMAT(200),ORT(25,2),NBC(25), NFIX(25)
1,R1(200),SK(200,40) 2,R(3)
С
С Считыванне н печать заголовка и контрольных данных
READ(5,7)TITLE ц
WRITE(6,100)TITLE 13
READ(5,1)NP,NE,NB,NLD,NDF,NMAT,I1 WRITE(6,1)NP,NE,NB,NLD,NDF,NMAT,I1
С
С Считывание и печать характеристик материала
READ(5,8) (N,(0RT(N,I),I = 1,2),N = I,NMAT) WRITE(6,108) 17
.WRITE(6,8) (N,(0RT(N,I),I= 1,2),N=. 1,NMAT)
С Считывание информации об узлах
READ(5,2) (N,(CORD(N,M),M= 1,2),N= 1,NP)
1 ...
20 21 22 [
23 ]
24 25 26 27

