Главная страница сайта
Российские промышленные издания (узловые агрегаты)
1 ...
19 20 21 [
22 ]
23 24 25 ...
27 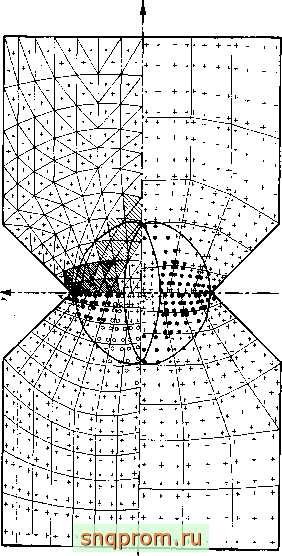
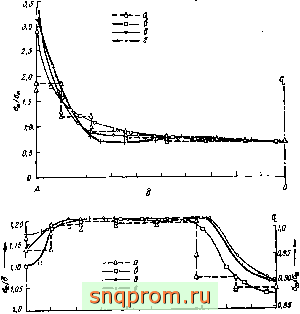
Фиг. 18.20. Характеристика различны.х элементов при упругопластическом расчете плоского напряженного состояния образца с выточками. Пластическая зона: а -треугольный элемент, <т^/а=:1Л86 н 1.226; б-линейный четырехугольник, а^/о==1,18б и 1,226; в-квадратичный четырехугольник, afd=l,I86; е-кубичный четырехугольник. 0/0=1,186 (а^ -среднее напряжение в выточке, одноосное
напряжение текучести, идеальная пластнчаость). Распредемние напряжений в ослабленном сечении: 5 -упругое решение; в-упругопла-стическое решение, a/dliise. Число степеней свободы во всех четырех случаях Примерно одинаково (172-178).
вопрос настолько обширен и практическое значение его так велико, что осветить его в одной главе невозможно. Для различных материалов можно предложить и экспериментально подтвердить различные формы определяющих уравнений. К,ак только установлены определяющие уравнения, к ним можно приспособить описанные в этой главе стандартные методы. Действительно, можно создать стандартные' программы решения задач для материалов с различными свойствами, в которые характеристики, определяющие особенности поведения материала, В!(одят в виде черного ящика .
Таким образом можно рассматривать такие явления, как вязкопластичность (пластические деформации зависят от времени) или различные задачи механики грунтов и горных пород [44].
Необходимо еще раз напомнить, что при решении нелинейных задач а) возможна неединственность решения; б) априори никогда нельзя гарантировать сходимость; в) стоимость решения значительно выше стоимости решения линейных задач.
Для преодоления первых двух трудностей необходимо понимание физической сущности задачи, а стоимость может быть снижена в результате дальнейших усовершенствований методов. В приведенных примерах применялись лишь простейшие конечные элементы. Очевидно, что при использовании этих методов можно применять любые функции формы элементов. Последние работы показывают, что использование рассмотренных в гл. 7 и 8 сложных элементов даже в двумерных задачах может дать значительную экономию [45].
На фиг. 18.20 сравниваются результаты расчета пластических зон при использовании элементов с постоянным распределением напряжений и изопараметрических элементов. Гладкость границ пластических зон (определенных по точкам Гаусса) в последнем случае приводит к значительному ускорению сходимости и повышению точности.
Наконец, следует отметить, что описанные методы удобно использовать и для решения линейных задач, сформулированных первоначально с использованием других значений постоянных. Привлекательность такого подхода не очевидна до тех пор, пока мы не рассмотрим, например, решение задачи теории упругости для материала с коэффициентом Пуассона, равным 0,5. Ранее отмечалось, что в этом случае матрица [D] становится неопределенной и необходимо использовать специальные приемы (см., например, гл. 4, разд. 4.5). Можно, однако, решать задачу теории упругости с допустимым значением коэффициента Пуассона методом начальных деформаций, изменяя в процессе решения деформации так, чтобы удовлетворить условию несжимаемости [34, 36].
ДРУГИЕ НЕЛИНЕЙНЫЕ ЗАДАЧИ
18.10. Нелинейные квазигармоннческие задачи теории поля
Нелинейности возникают в различных задачах теории поля рассмотренного в гл. 15 типа. Например, в задачах, описываемых уравнением [см. (15.1)]
проводимость k может зависеть от функции ф или ее градиентов. В качестве иллюстрации можно привести два типичных примера. Во-первых, при фильтрации жидкости скорость может не удовлетворять условию ламинарности (Дарен), в соответствии с которым она определяется выражениями
(18.46)
Vx = k И т. д.
В случае турбулентности требуется учитывать зависимость потери напора (grad) от более высокой степени скоростей. Такие законы получены, например, в работах [47] и [48]. Их можно также записать в виде (18.46), полагая [49-51]
Аналогичная ситуация возникает в задачах магнитостатики, где - магнитный потенциал, а * -величина, обратная магнитной проницаемости, которая существенно зависит от градиентов магнитного поля [52].
Таким образом, в обеих задачах уравнения, по существу, одинаковы.
Хотя очевидно, что термины переменные параметры упругости , начальные напряжения н деформации в этих случаях не подходят, для решения можно использовать аналогичные итерационные методы (см. разд. 18.3). В гл. 15 [уравнение (15.14)1 показано, что после дискретизации уравнения принимают такой же вид, как и в задачах теории упругости:
Ш = [Я]Ш + {/}=0. (18.47)
Поскольку k используется при вычислении матрицы [Я], получаем
[Я] = [Я({})]
и задача, таким образом, относится к рассмотренному в разд. 18.3 классу.
Для решения можно использовать итерационный метод Ньютона, вычисляя на каждом шаге
ДШ.и = -[Я„]-{т|(т.)}- (18.48)
В этом случае, как было показано ранее, при каждой итерации приходится обращать различные матрицы. Можно также применять модифицированный метод Ньютона - Канторовича, вычисляя
(18.49)
где [Яо] - матрица, полученная на первом шаге. Опять можно использовать различные способы ускорения сходимости [2]. кш-
логия с методами постоянной и переменной жесткости решения задач теории упругости очевидна.
До сих пор методы конечных элементов для подобных задач применялись сравнительно мало. Волкер [49] получил решение задачи, о неламинарном течении жидкости в пористой среде с помош,ью первого из описанных методов (с переменной матри-
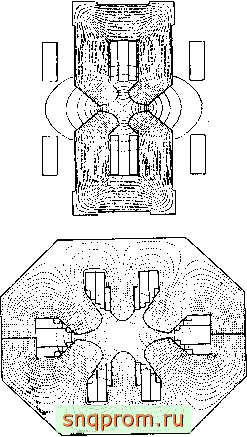
фиг. 18,21. JVlarHHTHoe поле в шестиполюйном магните с нелинейностью, об-у(;ловл?нной насыщением [52],
ней [Н]). Удовлетворительные результаты получены после небольшого числа итераций. Винслоу [52] использовал аналогичный метод для решения различных задач магнитостатики. На фиг. 18.21 показаны некоторые полученные им довольно интересные поля в нелинейном материале ).
18.11. Некоторые другие возможные применения
Ясно, что описанные в предыдущем разделе методы решения нелинейных уравнений могут непосредственно применяться и для других задач, например для задач теплопроводности с ярко выраженной зависимостью коэффициентов теплопроводности от температуры при повышенных температурах.
Однако очевидно, что эти методы имеют более широкие возможности в других физических задачах. Примером такой задачи является задача о ламинарном течении неньютоновских жидкостей, уравнения которой, по существу, совпадают с уравнениями вязкого ламинарного течения, рассмотренными в разд. 15.6 гл. 15, но вязкость в этом случае зависит от градиентов скорости.
Читатель может проявить свою изобретательность, применяя изложенные методы к подобным и многим другим задачам.
ЛИТЕРАТУРА
1. Zienkiewicz О. С, Valliappan S King 1. P., Stress Analysis of Rock as
a No-Tension JVtaterial, Geotechnique, 18, 56-66 (1968). 2a, Irons B. M Tuck R. C, A Version of the Aitken Accelerator for Computer
Iteration, Int. J. Num. Meth. Eng., 1, 275-278 (1969). 2b, Zienkiewicz O. C, Irons B. JVl., JVlatrix Iteration and Acceleration Processes
in Finite Element Problems of Structural Mechanics, Ch. 9 in: Numerical
Methods for Non-Linear .Algebraic Equations, Rabinowitz P ed Gordon and
Breach, 1970.
3, Oden J. T Numerical Formulation of Non Linear Elasticity Problems, Proc. Am. Soc. Civ. Eng., 93, ST3, 235-255 (1967).
4, Von Miaes R., Mechanik der Plaatischen Formanderung der Kristallen, Z. angew. Math. Mech., 8, 161-185 (1928),
5, Drucker D. C, A More Fundamental Approach to Plastic Stress-Strain Solutions, Proc. 1st. U. S. Nain. Cong. Appl. Mech., 487-491 (1951).
6, Koiter W. Т., Stress-Strain Relations, Uniqueness and Variational Theorems for Elastic Plastic .Materials with a Singular Yield Surface. Q. Appl. Math., 11, 350-354 (1953); есть русский перевод: Койтер, Соотношения между напряжениями и деформациями, вариационные теоремы и теорема едии-ствеиностн для упруго-пластических материалов с сингулярной поверхностью текучести. Механика, 2, № 60, стр, 117-121 (1960).
7, Johnson W Mellor P. W Plasticity for Mechanical Engineers, Van Nost-rand, Princeton, 1962.
8, Yamada Y Yoshimura N., Sakurai T Plastic Stress-Strain Matrix and Its Application for the Solution of Elastic-Plastic Problems by the Finite Element Method, Int. 1. Mech. Sci., 10, 343-354 (1968).
) В обеих работах уравнения решались итерационным методом, что предопределило выбор метода, в котором используется переменная матрица [ ],
9. Zienkiewicz О. С, Valliappan S., King I. P., Elasto-Plastic Solutions of Engineering Problems. Initial-Slress, Finite Element Approach, Int. J. Num. Meth. in Eng.. 1, 75-100 (1969).
10, Gallagher R, H., Padlog J.. Bijlaard P. P., Stress Analysis of Heated Complex Shapes, /. Am. Rocket Soc, 32 , 700-707 (1962); есть русский перевод: Галлагер, Падлог, Бейлард, Анализ напряжений в коистр)-кииях сложной формы, подверженных нагреву, Ракетная техника, 32, № 5, стр. 52-61 (1962).
11 Argyris J Н., Elasto-Plastic Matrix Displacement Analysis of Three-Dimensional Continua, /. Roy. Aero. Soc, 69, 633-635 (1965).
12. Pope G G. A Discrete Element Method for Analysis of Plane Elasto-Plastic Strain Problems, R. A. E. Farnborough, T. R. 65028, 1965.
13a Swedlow J. L. Williams M. L., Yang W. M., Elasto-Plastic Stresses in Cracked Plates, Calcit, Rept. SM. 65-19. California Inst, of Technology, 1965.
136. Swedlow J. L., Elastic Plastic Cracked Plates in Plane Strain, Int. J. fracture Mech., 5, 33-44 (1969).
14. Marcal P. V., King I. P., Elastic-Plastic Analysis of Two Dimensional Stress Systems by the Finite Element Method, Inf. J. Mech. Sci., 9, 143-155 (1967).
15. Reyes S. F., Deere D. U., Elasto-Plastic Analysis of Underground Openings by the Finite Element Method, Proc. 1st Inf. Congr. Rock Mechanics, II, 477-486, Lisbon (1966).
16. Popov E. P., Khojasteh-Bakht M., Yaghmai S., Bending of Circular Plates of Hardening Material, Intern. J. Sot. Struct., 3, 975-988 (1967).
17. Argyris J. H., Scharpf D. W., Methods of Elasto-Plastic Analysis, Symp. on Finite Element Techniques, Stuttgart, June 1969.
18 Theokaris P. S. Marketos E., Elastic-Plastic Analysis of Perforated Thin Strips of Strain-Hardening Material, J. Mech. Phys. Sol., I2, 377-390 (1964),
19 Drucker D C, Prager W., Soil Mechanics and Plastic Analysis or Limit Design, Q. Appl Math., 10, 157-165 (1952).
20 Bishop A, W., The Strength of Soils as Engineering Materials, Geotechni-que, 16, 91-128 (1966),
21. Zienkiewicz O. C, Continuum Mechanics as an Approach to Rock Mass Problems, Ch. 8 in: Rock Mechanics in Engineering Practice, Stagg K. G., Zienkiewicz O, С eds Wilev, 1969,
22. Valliappan S Non-Linear Stress Analysis of Two-Dimensional Problems with Special Reference to Rock and Soil Mechanics, Ph. D. Thesis, Univ. of Wales. 1968,
23 Mroz Z., Non Associated Laws in Plasticity, 1. Mec. and Phys. Appl., 2, 21-41 (1963).
24. Davis E. M., Theories of Plasticity and the Failure of Soil Masses, Ch. 6 in; Soil Mechanics. Lee I. K., ed., Butterworth, 1969.
25a. Zienkiewicz O. C, Best В., Some Non-Linear Problems in Soil and Rock Mechanics -Finite Element Solution, Conf. on Rock Mechanics, Univ. of Queensland, Townsville, June 1969.
25b. Zienkiewicz O. C, Best В., DuIIage C, Stagg K. G., Analysis of Non-Linear Problems in Rock Mechanics with Particular Reference to Jointed Rock Svstems, Proc. 2nd Int. Congress on Rock Mechanics, Belgrade, 1970.
26. Valliappan S., Nath P., Tensile Crack Piopagation in Reinforced Concrete Beams by Finite Element Techniques, Int. Conf. on Shear Torsion and Bond in Reinforced Concrete, Coimbatore, India, Jan. 1969.
27 Krahl N. W., Khachaturian W., Seiss C. P., Stability of Tensile Сгаскз in Concrete Beams. Proc. Am. Soc. Civ. Eng., 93, STl, 235-254 (1967).
28. Goodman R. E., Taylor R. L.. Brekke T A Model for the Mechanics of Jointed Rock, Proc. Am. Soc. Civ. Eng., 94, SM3, 637-659 (1968).
29. Scholes A., Strover E. M., The Piecewise Linear Analysis of Two Connected Structures Including the Effect of Clearance at the Connections, Int. J Num. Meth. in Eng., 3, 45-52 (1971).
30. Mendelson A., Hischberg M. H., Manson S. S., A General Approach to the Practical Solution of Creep Problems, I. of Basic Engineering, Trans. ASME, Series D, 81, 585-598 (1959).
31. Zienkiewicz O. C, Watson M., King I. P., A Numerical Method of Visco-Elastic Stress Analysis, Inf. J. of Mech. Sci, lO, 807-827 (1968).
32. Zienkiewicz O. C, The Finite Element Method in Structural and Continuum Mechanics, Ist ed., McGraw-Hill, 1967.
33. Greenbaum G. A., Rubinstein M. F., Creep Analysis of Axi-Symmetric Bodies Using Finite Elements, Nucl. Eng. and Design, 7, 379-397 (1968).
34. Treharne G. Applications of the Finite Element Method to the Stress Analysis of Materials Subject t.o Creep, Ph. D. Thesis, Univ. of Wales, Swansea, 1971.
35. Lee E. H., Viaco-EIasticity in: Handbook of Engineering Mechanics Flue-ge W., ed., McGraw-Hill, 1962. в в , в
36. Lee E. H., Radok T. R. M., Woodward W, В., Stress Analysis for Linear Visco-Elastic Materials, Trans, of the Soc. of Rheology, 3, 41-59 (1959),
37. Leckie F. A., Martin J, В., Deformation Bounds for Bodies in a State of Creep, {.Appl Mech., ASME, 411-417 (June 1967); есть русский перевод; Леккн, Мартин, Оценки для поля деформаций прн noлзvчecтн. Труды Амерн-каискогообщества инженеров-механиков. Прикладная механика, Кя2 (1967)
38. Finnic I., Heller W. R., Creep of Engineering Materials. McGraw-Hill, 1959
39. Johnson A. E Complex Stress Creep, Met. Rev., 5, 447 (I960),
40. Frederick C. 0 Chubb E. J Bromley W, P., Cyclic Loading of a Tube with Creep, Plasticity and Thermal Effects, Applied Mechanics Convention, Proc. Inst. Mech. Eng., I80, 31 (1965).
41. Zienkiewicz O. C, Analysis of Visco-Elastic Behaviour of Concrete Structures with Particular Reference to Thermal Stresses, Proc. Am. Concr. Inst. 58, 383-394 (1961).
42. Hilton H. H., Ru3sell H, G., An Extension of Alfreys Analogy to Thermal Stress Problems in Temperature Dependent Linear Viaco-elastic Media /. Mech. Phys. Solids, 9, 152-164 (1961).
43. Zienkiewicz O. C, Watson M., Cheung Y. K.. Stress Analysis by the Finite Element Method - Thermal Effects, Proc, Conf, on Prestressed Concrete Pressure Vessels, Inst, Civ. Eng., London, 1967.
44. Malina H.; Berechnung von Spannungsumlagerungen in Fels und Boden mil Hilfe der Elementenmethode, Veroffentlichungen Univ Karlsruhe 40 1-90 (1969).
45. Nayak 0. C., Plasticity and Large Deformation Problems by Finite Element Method. Ph. D. Thesis, Univ. of Wales, Swansea, 1971.
46. Zienkiewicz O. C, Valliappan S., Analysis of Real Structures for Creep, Plasticity and Other Complex Constitutive Law3, Conf. on Materials in Civ. Eng., Univ. of Southampton. 1969.
47. Forchheimer P. H., Wasserbewegung durch Boden, Zelt Ver Dt Ing 1782 (1901).
48. Muskat M The Flow of Homogeneous Fluids Through Porous Media J. W. Edwards Inc., 1946.
49. Volker R. W., Numerical Solutions to Problems of Nonlinear Flow Through Porous Media, Ph. D, Thesis, Univ. of Queensland, Townsville, 1969.
50. Volker R. W., Non-Linear Flow in Porous Media by Finite Elements, Proc. Am. Soc. Civ. Eng., 95, HY, 2093-2114 (1969).
51. Ahmed N., Suneda D. K., Non-Linear Flow in Рогоиз Media, Proc. Am Soc Civ. Eng., 95, HY6, 1847-1859 (1969).
32. Winslow A. M., Numerical Solution of the Quasi-Linear Poissons Equation in a Non-Uniform Triangle Mesh, /. Сотр. Physics, I, 149-172 (1967).
19.1. Введение
В предыдущей главе рассматривались нелинейности, обусловленные свойствами материала, и были описаны итерационные методы решения нелинейных задач, в которых используются обычные линейные соотношения. В этой главе такой же подход будет применен к исследованию геометрической нелинейности.
Во всех рассмотренных ранее задачах предполагалось, что и перемещения и деформации конструкций малы. Практически это означает, что форма элементов в процессе нагружения не изменяется и что для деформаций можно использовать приближенные линейные соотношения.
На практике эти предположения часто приводят к неправильным результатам даже при малых деформациях, не превышающих предел упругости материала конструкции. При точном определении перемещений ряда конструкций может оказаться необходимым учет геометрической нелинейности. Например, мембранные напряжения, которыми обычно пренебрегают прн изгибе пластин, могут явиться причиной значительного уменьшения перемещений даже 1.ри малых деформациях. С другой стороны, может оказаться, что нагрузка, при которой прогиб увеличивается, достигается быстрее, чем это предсказывается линейной теорией, и может возтикнуть ситуация, в которой прн продолжающемся деформиров :ин несущая способность будет падать. Это не что иное, как к. ассическая задача устойчивости конструкций. Такие задачи встречаются довольно часто. Значение их особенно велико в авиационной н космической технике, при конструировании радиотелескопов, градирен н других тонкостенных конструкций.
Кроме того, во многих случаях могут иметь место большие перемещения при малых деформациях. Типичным примером такого типа является классическая задача о гибких телах, как, например, о часовой пружине.
В этой главе предпринята попытка подойти ко всем этим задачам с единых позиций и указать общие методы исследований.
Однако ни один из вопросов, связанных с геометрической нелинейностью, подробно в этой главе не рассматривается. Это вопрос о больших, хотя и упругих деформациях таких материа-
лов, как резина и т. п. В этом случае необходимо использовать специальные соотношения между напряжениями и деформациями. Ограниченный объем книги не позволяет, подробно остановиться на этом вопросе. Тем не менее общий подход, описанный в следующем разделе, можно применить и к таким задачам, если использовать соответствующие законы связи напряжений с деформациями.
Геометрическая нелинейность часто может сочетаться с нелинейностью физического типа, рассмотренной в предыдущей главе, такой, как пластичность при малых деформациях н др. В принципе это не приводит к дополнительным трудностям, и методы, изложенные в этой главе, легко могут быть применены и к таким задачам.
19.2. Общие положения
19.2. J. Основная задача
Независимо от того, велики или малы перемещения (нлн деформации), внутренние и внешние силы должны удовлетворять условиям равновесия. Если в соответствии с изложенным в гл. 2 перемещения определяются конечным числом (узловых) параметров {6}, то, как показано там и повторено в предыдущей главе [см. соотношение (18.13)], должно выполняться равенство
({б})} = J [ВГ {<У] dV - т = о, (19.1)
где {ф} -сумма внешних и внутренних обобщенных снл, а матрица [В] определяется из соотношения
d{B} = [B]d{6).
(19.2)
Черта означает, что прн больших перемещениях деформации нелинейно зависят от перемещений и матрица [В] зависит от {б}, В дальнейшем будет видно, что ее удобно представить в виде
[S] = [So] + [Bi({6})], (19.3)
где [Во] - матрица, определяющая бесконечно малые деформации, а матрица [Bl] зависит от перемещений. Будет показано, что в общем с^учае [BJ является линейной функцией пере.че-щений, .
ГЕОМЕТРИЧЕСКИ НЕЛИНЕЙНЫЕ ЗАДАЧИ; БОЛЬШИЕ ПЕРЕМЕЩЕНИЯ И НЕУСТОЙЧИВОСТЬ КОНСТРУКЦИЙ
Если деформации не очень велики, то можно использовать обычное соотношение теории упругости
{а} = 10] {{8} - {ез}) + {оо},
(19.4)
где [О] -обычная матрица упругих постоянных).
Однако в равной степени можно было бы использовать и любое нелинейное соотношение между напряжениями и деформациями, поскольку задача сводится к решению нелинейной системы уравнений (19.1).
Вероятно, нет необходимости повторять, что интегрирование в (19.1) фактически производится по отдельным элементам, а их вклады в уравнения равновесия в узлах суммируются обычным образом.
19.2.2. Итерационные методы
Ясно, что уравнение (19,1) следует решать методом итераций, и возможность применения описанных в предыдущей главе (разд. 18,3) общих методов очевидна.
При использовании метода Ньютона необходимо, как уже указывалось, найти зависимость между d[6} и d {ф}. Варьируя (19.1) по d{6}, получаем
{ф} = J [BY {а} dV + 5 [BY rf {a} dV. (19.5)
Используя формулы (19.4) и (19.2), находим ) rf{a} = [Z)]rf{8} = [Z)] [S]rf{6}, а на основании (19.3) имеем
Поэтому
где
rf[S]=rf[SJ.
d=\d[BLY{o)dV-{-[K]d[b), (19.6)
[K\=\[BY[D\[B\dV = [Ko\ + [KlI (19.7)
) Необходимо иметь в виду, что компоненты напряжения, определяемые соотношением (19.4), соответствуют используемым компонентам деформации. В некоторых задачах о больших перемещениях эти компоненты деформации отнесены к направлениям, значительно отличающимся от иаправлеиий первоначальных фиксированных координат.
) Если используется нелинейное соотношение между напряжениями и деформациями, то [О] = [0({а))] - матрица упругих постоянных для приращений, определяемая равенством (18.15).
а [Яо] является обычной матрицей жесткости при малых деформациях, т. е. [Ко] имеет вид
[K,]=\[BoY[D][B,]dV.
(19.7а)
Матрица [Кь] появляется благодаря тому, что перемещения велики. Она определяется выражением
[Kl\ = \ {[BoY [D] [ВЛ + [BlY[D][вj +
[BLY[D][B,])dV. (19.76)
Матрица [Я] известна как матрица начальных перемещений [2], матрица больших перемещений и т. п. Нетрудно показать, что эту матрицу можно построить, считая деформации малыми, но учитывая изменения координат элемента при вычислении жесткостей.
Первый член выражения (19.6) может быть записан в виде
(19.8)
\d[Bi.Y{a}dV[Ka]d{b},
где [Яо] - симметричная матрица, зависящая от величины напряжения (в справедливости этого утверждения, вероятно, лучше всего убедиться на конкретных примерах). Эта матрица известна как матрица начальных напряжений [2] или геометрическая матрица [3, 4]. Таким образом,
d {Щ = ([/Со] + [КЛ -f [Kl]) d {6} = [Кт\ d Щ, (19.9)
где [Ст-]-полная матрица тангенциальных жесткостей. Итерации метода Ньютона строятся, как описано в разд. 18.3:
а) в качестве первого приближения {6} строится решение по линейной теории упругости;
б) с помощью соотношения (19.1) определяется для заданной матрицы [В] и напряжений, определяемых равенством (19.4) (или любым другим линейным или нелинейным законом);
в) строится матрица [Кт];
г) определяется поправка
д{б}, = -[я,]-№..
Процесс повторяется до тех пор, пока величина не станет достаточно малой,
И здесь возможно использование постоянной матрицы, если на каждом шаге правильно вычислять {\;}г, [5]. Хотя применение этого метода решения сокращает затраты машинного вре-
менн, число итерации увеличивается и метод сходится во многих случаях медленно.
Все решения можно находить за один шаг для полной действующей нагрузки. Однако, как и во всех нелинейных задачах, возникает возможность неединственности решения и при этом может быть найдено решение, не имеющее физического смысла. В таких случаях целесообразно задавать нагрузку отдельными приращениями и получать нелинейное решение для каждого приращения. С вычислительной точки зрения это часто экономичнее, поскольку эффекты нелинейности на каждом шаге становятся меньше. Если приращения нагрузки достаточно малы по величине, то каждое решение в приращениях с достаточной степенью точности может быть найдено за один шаг [3, 4, 6]). Однако необходимо периодически проверять выполнение условия равновесия с помощью нелинейного соотношения (19.1).
19.2.8. Задача начальной устойчивости
Интересно отметить, что матрица [Ка] не содержит перемещений в явном виде и пропорциональна величине напряжения {а}. Если на первом шаге вычислений {о} определяется из линейного решения, то в соответствии с (19.6)
с1Ш = ([Ка]-\-Ш)(1{6}, (19.10)
поскольку при этом [/Ci.l==0.
Если нагрузки увеличить в Я раз, то можно найти, что существует нейтральное состояние равновесия, т. е. такое, при котором
dH}{[Ko] + mc]}d{6}0. (19.11)
Решая описанную выше (см. гл. 17) типичную задачу о собственных значениях, можно найти К.
Это не что иное, как классическая задача начальной устойчивости (выпучивание стоек, пластин, оболочек и т. д.).
В литературе довольно часто этот метод используется там, где он неприменим. Описанная задача начальной устойчивости может дать физически правильное решение только в том случае, если деформации, определенные из упругого {[Ко]) решения, таковы, что матрица больших деформаций [Кь] тождественно равна нулю. Это может быть только в очень ограниченном числе представляющих практический интерес случаев (например, идеально прямая стойка под действием осевой силы; замкнутая
) Это обстоятельство фактически указывает на то, что описанный метод эквивалентен методу Эйлера. Ясно, что его можно уточнить, применяя методы Рунге - Кутта или методы проб и ошибок [28].
сфера, нагруженная равномерно распределенным давлением, и т. д.). Полученные с помощью этого метода выводы о начальных несовершенствах применимы только в тех случаях, когда возможна бифуркация равновесия. Для технических приложений такие задачи необходимо исследовать, используя полную матрицу тангенциальных жесткостей [6]. Состояние нейтрального равновесия достигается тогда, когда величина [KT]d{6] тождественно равна нулю. Ясно, что в этом случае следует использовать метод приращений.
19.2.4. Энергетическая интерпретация критериев устойчивости
Как было показано в гл. 2, виртуальная работа прн изменении перемещения на величину d(6} фактически равна вариации полной потенциальной энергии х- Таким образом, в состоянии равновесия
dx = d{6Y{}=0, (19.12)
т. е. полная потенциальная энергия стационарна [что эквивалентно уравнению (19.1)].
Вторая вариация х в соответствии с (19.9) имеет вид
dh = d (dt) = d {bfd {} = d {ЬУ [К A d{b). (19.13)
Критерием устойчивости является положительность величины этой второй вариации, и, наоборот, ее отрицательность является критерием неустойчивости (поскольку в первом случае конструкции должна бы:ь сообщена энергия, а во втором - у конструкции избыток энергии). Другими словами, если матрица [Кт] положительно определенная, то состояние равновесия устойчиво. Этот- критерий хорошо известен и широко используется при исследовании устойчивости в случае больших деформаций ) [7-9].
19.2.5. Силы, зависяш,ие от деформации
При выводе формулы (19.5) предполагалось, что силы [R] не зависят от деформации. В некоторых случаях это не так. Например, к категории зависящих от деформаций нагрузок относятся давление, действующее на сильно деформируемую конструкцию, и некоторые аэродинамическиесилы (при флаттере).
) Другой, хотя и реже используемой проверкой является исследование знака определителя матрицы 1Кт\-
Если СИЛЫ зависят ОТ перемещения, то в (19.5) необходимо добавить вариацию d{R} по d{6}. Учет этого члена позволит исследовать задачи об устойчивости и о больших деформациях под действием таких (неконсервативных) нагрузок.
19.3. Большие прогибы и начальная устойчивость пластин
19.3.1. Определения
В качестве первого примера рассмотрим задачи, связанные с деформацией пластин, нагруженных поперечными силами и

Фиг. 19.1.
а-результирующие мембранных и изгибных напряжений плоской пластины; б-удлинение срединной поверхности прн поперечном перемещении.
силами В плоскости пластины, когда перемещения конечны, но не велики. Известно, что в таких случаях перемещения в поперечном направлении вызывают деформации мембранного типа, и задачи о деформации в плоскости и в поперечном направлении уже нельзя рассматривать отдельно, поскольку оии являются связанны.чи.
Как и ранее, деформаций пластины будем характеризовать перемещениями срединной поверхности; если, как показано на
фиг. 19.1, а, плоскость х, у совпадает со срединной поверхностью, то (см. гл. 10 и 11))
{8} =
Уху
dw дх d w ду
Ту Тху
(19.14)
В частности, = Cxt, где - среднее мембранное напряжение. Если рассмотреть деформированную пластину (фиг. 19.1,6), то можно увидеть, что перемещение w приводит к дополнительному растяжению' срединной поверхности в направлениях X и у и элемент длины dx растягивается до величины
т. е. удлинение в направлении х можно записать (с точностью до членов второго порядка) в виде
ди , ] f dw \2
Рассматривая таким же образом и другие компоненты [10], деформацию можно представить в виде
{е} =
ди дх ду ду
ди , до ду дх dw
дх- дЫ ду
1 (2е^
iiay )
( dw \/dw \дх Жду
о
о о
19.15)
) Мембранные и изгибающие компоненты помечены индексами р1 а Ь.
Здесь первый член представляет собой уже неоднократно рассмотренное линейное выражение, а второй содержит нелинейные члены. В этом выражении и, V, w - перемещения срединной поверхности.
Если рассматривается линейно-упругое поведение, то матрица [D] состоит из мембранных и изгибающих компонент (см, гл. 4 и 10):
rrnpi о
[£)
О
(19.16)
Перемещения с помощью соответствующих функций формы выражаются через узловые параметры. Например,
(19,17)
Множество узловых параметров удобно разделить на части, определяющие мембранные и изгибные деформации:

где
{бП = { (как в гл. 4),
(19.18)
dw
(как в гл. 10).
\ ду li
функцию формы также удобно представить в виде
О
L о [Ntfi
(19.19)
мы будем считать, что и вектор перемещений тоже имеет вид, соответствующий (19.18).
Такие представления удобны, поскольку все характеристики, за исключением нелинейной деформации (ерг}, совпадают с обычными линейными.
19.3.2. Вычисление матрицы-Щ
Для дальнейшего необходимо получить выражения для матриц [В\ и [Кт]- Сначала отметим, что
Й = [Во] + [Вл1, [BS] О
где
(19.20)
[Во]-
L О ыи
, [BJ =
О [Bi] Lo О J
причем [Во], [Во] -обычные известные матрицы, соответствующие линейным элементам при плоском напряженном состоянии и изгибе, а [В*] находится варьированием {ej по па-рамет[уам {б*}.
Эту нелинейную компоненту деформации из выражения (19.15) удобно записать в виде
=тИ]{9}. (19.21)
Производные (углы наклона) w можно связать с узловыми пара-меграми {б*}:
где
{9} =
[С] =
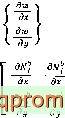
= [0]{б^
(19.22)
(19.23)
Матрица [G] зависит только от координат. Варьируя (19.21), получаем)
{р/} = У И! {6} + Y[A]d {6} = [А] d {0} =
= mG]d{b},
(19.24)
) При получении (19.24) использовано интересное свойство матриц М] и {9}. Легко проверить, что если
(19.25)
и, следовательно, по определению
[ВП = 1А]10].
19.3.3. Вычисление матрицы [Кт]
Матрицы, связанные с линейной (малой) деформацией, записываются в виде
KS О . О Ко.
(19.26)
в соответствии с определениями, приведенными в гл. 4 и 10. Матрицы связанные с большими перемещениями, можно получить, подставляя (19.20) в (19.76). После некоторых преобразований имеем
О Ш ID} iBlV
[К
Симметрично [bIJ [D] [fit].
dV. (19.27)
Матрица [/CJ находится в соответствии с определением (19.8). Варьируя (19.20), получаем
О О
IdlBiY о.
(19.28)
есть произвольный вектор, то
d [А] {х] =
Таким образом. Аналогично если
О
At) ii)-
dlA]ifi] = [A]d
0 -1
X2 Xl
d [Af [y] -
yi Уг lyi Ы
die);
STO второе свойство будет использовано позднее.
а после подстановки в (19.8) и (19.25) находим
lK ]d{6}=\
О О l[GYd[AY Oj
М,у
(19.29)
В соответствии со свойством, изложенным в примечании иа стр. 447, можно записать
d[AY< Ту
т
i- ху
rf{9} =
Т
lG]d{6}.
Таким образом, окончательно получаем
О О
где
Lo ШГ
Тх т
(19.30)
(19,31)
известная симметричная матрица для начальных напряжений пластин.
19.3.4. Задача о больших прогибах
Все необходимые соотношения для решения задачи о больших прогибах пластины уже получены.
На первом этапе находятся перемещения (6} из решения несвязанной задачи о малых перемещениях. С их помощью определяются линейная и нелинейная [по соотношению (19.21)] части действительных деформаций. Соответствующие этим деформациям напряжения находятся из обычных соотношений теории упругости, а затем из уравнения (19.21) определяется {i)o}. Для последующих приближений [Кт] строится по формулам (19.26), (19.27) и (19.30).
Полученное таким образом решение типичной задачи [9] (фиг. 19.2) показывает, что с увеличением деформации благодаря появлению мембранных напряжений пластина становится жестче. Перемещения краев пластины как в ее плоскости, так и в поперечном направлении отсутствуют. Результаты расчета хорошо согласуются с аналитическим решением,
1 ...
19 20 21 [
22 ]
23 24 25 ...
27

