Главная страница сайта
Российские промышленные издания (узловые агрегаты)
1 ...
18 19 20 [
21 ]
22 23 24 ...
27 mm t.D
Фиг. 18.6. Консольная балка. Плоское напряженное состояние, идеальная пла-стичность. Пластические зоны для различных отношений Р/Рс (Рс-критическая нагрузка, вычисленная по балочной теории пластичности).
-0.2 О 0,2 0.i перемещение в С а
0,6 0,8
о
Сечение АА
О . 1 сечение вв
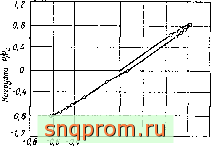
Фиг. 18.7. Консольная балка, показанная на фиг. 18.6. а-перемещения при изменении знака нагрузки; б -распределение напряжений xly
разлнчны.ч этапах разгрузки, о при начале текучести; X при максимальной нагрузке; Д при максимальной нагрузке с обратным знаком; □ остаточные напряжения.
НИЯ показанный на фиг. 18.7, а гистерезис перемещения и остаточные напряжения после снятия нагрузки, обусловленные пластическим деформированием.
На фиг. 18.8 представлено графически из.менение перемещений при возрастании нагрузки. По мере приближения к критической нагрузке требуется все большее число итераций, и при PIPc - 1 процесс не сходится. Таким образом, хотя нелинейное решение дает возможность найти нижнюю границу критической нагрузки (путем удовлетворения условиям равновесия и текучести), метод приращений нагрузок не позволяет установить ее истинную величину. Для лучшего описания критического поведения балки проще задать некоторые перемещения в точке приложения нагрузки и затем
СхоВитсти нет
0,2 0,4 0.6 0.8 Перемещение в С
Фнг. 18.8. Консольная балка. Зависимость перемещения от Р/Рс.
увеличивать их, пока реакция в этой точке не перестанет возрастать. Этот прием рассмотрен в следую- cj щем примере.
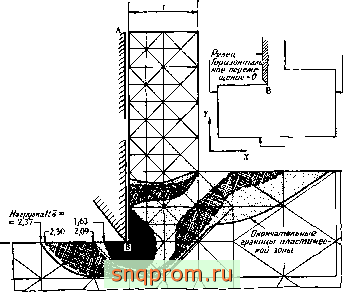
Пластическое течение а при резаиии металла. На фиг. 18.9а показана идеали- g зированиая схема обработки металлической заготовки резцом, снимающим с нее Стружку. Хотя в действительности эта задача связана с большими- перемещениями, решалась упрощенная упруго-пластическая
задача о поведении тела определенной формы при заданных постоянных перемещениях вертикальной поверхности. На фиг. 18.96 показаны пластические зоны, распределение нагрузки и полная нагрузка на резец. Видно, что вследствие идеальной пластичности материала при определенных перемещениях нагрузки увеличиваются до некоторых постоянных значений. При этом возникает критическое состояние, соответствующее отделению стружки. В рассмотренном примере только этот заключительный этап имеет практическое значение.
Материал Мора - Кулона. Туннель. Сходные с пластичностью явления наблюдаются во многих материалах, таких, как почва, скальные породы, керамические материалы и бетон. В них также может происходить необратимое деформирование при почти постоянных напряжениях. Однако поверхность текучести для этих материалов зависит не только от девиаторных (сдвиговых) напряжений, как в законе Мизеса, но и от величины среднего напряжения.
перемещение = 0-
ТЬение отсутствует-
Жесткое перемещение J
Вертикальное перемещение =0
Фиг. 18.9а. Приближеииое описание процесса обработки металла путем задания эквивалентных перемещений в месте среза, о - одноосное напряжение текучести, -Форма детали и пластические зоны.
Известный критерий Мора - Кулона, определяющий максимальное сдвиговое напряжение на произвольной площадке в виде
T = C + a,tg, (18.32)
где С -сила сцепления, а„ - нормальное напряжение и ф - угол внутреннего трения, можно приближенно'записать в более удобной форме, предложенной Друкером [19]:
(18.33)
где /f -первый инвариант тензора напряжений /, = ax-f-aj,+aa J2 - второй инвариант
J2=i ЦОх - Oyf 4- (Оу - ОгГ + {Ог - Cxf] + xly + + xL,
а и Я -постоянные, зависящие от сцепления и внутреннего трения материала. Постоянные, входящие в (18.33), связаны с
!/становившвеся воотсяние i

Перемещение
Нагрузка/tB2.37 -2,03

0,88 (упругое состояние)
~\---=~Jg=;
2 6 В
Распределение давления вдоль АВ
Ю
Фнг, 18,96. Приближенное описание процесса обработки металла. Зависимость полной нагрузки от перемещения и распределение давления на резец.
величинами в (18.32) соотношениями 2sin
3 (3 - sin ф)
6С COS Ф л/з'{3 - sin)
Другие возможные формы критериев подробно обсуждены в работе [20], однако для иллюстрации метода вполне достаточно рассмотреть форму, предложенную Друкером.
Если в дополнение к предположению о существовании такой поверхности текучести использовать ассоциированный закон, то
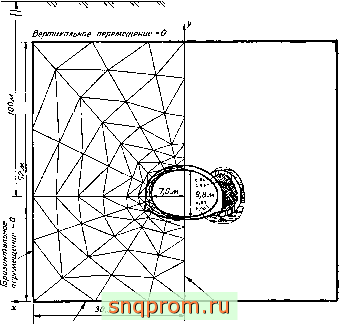
задачи расчета конструкций из подобных материалов можно решать с помощью описанных ранее методов. На фиг. 18.10 показано решение задачи о пластических зонах около туннеля, возникающих за счет перераспределения напряжений в резуль-
1 Поверхность земли
Гдризантальнае первмещение=0
Вертикальное пере/нещоние =0 а
Фиг. 18 10. Подкрепленный туннель, а -разбиеаие иа 15.! элемента с 94 узлами. Подкрепление: £=2,02 10 H/м^ v= ,15. Грунт: £=3,4 Шэ Н/м\ vt=v.,20, С=9.5 10 H/M ф=30°. Начальное напряжение (Jo=Yl
с началом при Л=124 м. ou=0,2Yft. V=6,9 Ш Н.м . б -пластические зоны.
тате выемки грунта. Аналогичные задачи рассмотрены в работах [9, 15,21 и 22].
Основная трудность решения таких задач связана не с вычислениями, а с формулировкой соответствующих определяющих уравнений. В частности, для материалов Мора - Кулона ассоциированный закон, как правило, не выполняется [23]. Их
поведение описывается так называемыми неассоциированными законами. В соответствии с простым предположением, сделанным Денисом [24], пластические деформации удовлетворяют соотношению
d{e}, = X[DA{a})r\ (18.34)
где [Do] - матрица, зависящая от уровня напряжений, сходная по структуре с матрицей упругости. Повторив описанные соотношениями (18.20) -(18.26) действия, получим новую упруго-пластическую матрицу, которая уже не будет симметричной [25]. Однако метод начальных напряжений применим и в этом случае.
1S.5. Материал, работающий только иа сжатие
Гипотетический материал, способный выдерживать только сжимающие напряжения и не сопротивляющийся растяжению при деформировании, во многих отношениях аналогичен идеально пластичному материалу. Хотя в действительности такой идеальный материал, вероятно, не существует, он хорошо аппроксимирует поведение насыпей из горных пород и других сыпучих материалов.
В явном виде соотношение между напряжениями и деформациями, как правило, записать не удается, однако достаточно воспользоваться соотношениями теории упругости, а при появлении растягивающих напряжений приравнять их нулю. При этом уместно использовать метод начальных напряжений, который фактически и был разработан для решения таких задач [1].
Схема вычислительного процесса очевидна, но важно помнить, что главные растягивающие напряжения должны исключаться.
Приведенные выше определяющие соотношения могут лишь приблизительно описывать реальное поведение материала, поскольку при этом не учитывается влияние нераскрытых трещин на перераспределение сжимающих напряжений. Однако ясно, что полученные результаты помогут все же изучить поведение реальных конструкций из сыпучих пород.
Подземная электростанция. На фиг. 18.11, а и б показан пример применения описанной модели в практической задаче. На фнг. 18.11,0 изображено распределение напряжений в районе подземной электростанции с учетом предварительно напряженной арматуры вблизи выработки, полученное в результате упругого решения. Там же указаны зоны растягивающих напряжений. Результаты решения этой же задачи (фиг. 18.11,6) при использовании модели материала, работающего только на сжатие, свидетельствуют о незначительном перераспределении напряжений и опасных зон.

V \ / Стрелкой ука-\ > зано растяжение
Растяжение I
J Зоны растрескиванш
Фиг. 18.11. Напряжения вблизи подземной электростанции при действии сил
тяжести с учетом предварительны. напряжений, о-упругие напряжения; б -напряжения, определенные для материала, работающего только на сжатие
Разновидностью такого материала может служить материал с конечным пределом прочности на растяжение, не обращающимся в нуль в момент появления трещин. Такой подход использовался в работе [26] при исследовании поведения балок из армированного бетона. Для предварительно напряженных балок
173 см-
Ислользованндя сетка
ccfeHueMe.ASCM
Растрескивание при максимальной нагрузке
Упругое

-140°
Упругое

Сжатие Растяжение А-А
в-в
Сечение, в котором нет трещин
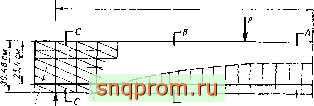
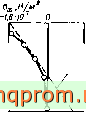
Фиг. 18.12. Образование трещин в балке Из предварительно напряженного бетона. Максимальное растягивающее напряжелие 1,55-10° Н/м^. Распределение напряжений в различных сечениях.
(без учета текучести при сжатии) получено очень хорошее совпадение с,экспериментальными результатами. На фиг. 18,12 показаны некоторые результаты для балки, испытанной в работе [27].
18.6. Слоистый материал и стыковочные элементы
В другой модели идеализированного материала предполагается. Что материал состоит из большого числа изотропных упругих слоев. При сжатии слои передают сдвиговые напряже-
ния, не г напряже! Ясно,
она имей На фи Если ось
для напр:
при ис-ю ниже,
случае, лоев, то , можно
Фиг. 18.13. Слоистый материал (а) и узкое слоистое соединение {б):
записать и
I Txtf I < liOy
(18.35а) (18.356)
Здесь ц - коэффициент трения между слоями.
Если упругие напряжения превышают предельные значения, определяемые соотношениями (18.35), то они должны быть уменьшены до этих значений.
Применение метода начальных напряжений для таких материалов опять не представляет затруднений. Задача аналогична рассмотренной в предыдущем разделе задаче о расчете материала, работающего только на сжатие. На каждом этапе упругого расчета проверяется наличие растягивающих напряжений Оу. Если такие напряжения возникают, то вводится поправочное начальное напряжение, сводящее их и касательные напряжения к нулю. Если же Оу - сжимающее напряжение, то производится проверка абсолютной величины касательных напряжений Гху'- В случае превышения значения, определяемого соотношением (18.35а), их уменьшают до предельно возможной величины.
Описанная математическая модель не всегда будет правильно отражать истинное поведение материала при разгрузке, поскольку сжимающие напряжения могут возникнуть лишь после исчезновения зазоров между слоями. Это затруднение (при нулевом коэффициенте Пуассона) можно устранить, контролируя появление растягивающих деформаций и используя вместо (18.356) соотношение
ау=0 при 8г,>0. (18.36)
В противном случае материал будет упругим. Это фактически один из вариантов деформационной теории пластичности.
Излишне говорить о том, что направления слоев могут меняться от элемента к элементу и таким методом можно исследовать сложное поведение горных пород со случайным расположением трещин,-
Введение прочности сцепления и коэффициента трения, зависящего от величины сдвиговой дефор.мации (обычно коэффициент трения уменьшается с увеличением сдвиговой деформации), требует незначительных изменений программы. Таким же образом можно исследовать размягчающиеся материалы [25].
В некоторых случаях описанный тип поведения наблюдается лишь в узкой области между однородными массивными упругими телами. Это, в частности, имеет место при геологических сдвигах или при наличии больших трещин в горной породе. В таких случаях удобно использовать узкие, как правило, пря-
6101
моугольные элементы, геометрическими характеристиками которых являются средние координаты концов А п В (фнг. 18.13,6) и толщина. Однако элемент соединяется с примыкающими те-- лами в четырех отдельных точках (1-4). Эти переходные элементы могут быть, как показано на фиг. 18.13, простыми прямоугольниками. Можно также использовать и изопараметрические элементы более сложной формы (см. гл. 8).
В работе [28] рассмотрены в некоторой степени похожие переходные элементы, использованные для исследования устойчивости насыпей из горных пород. Однако описанные здесь переходные элементы имеют более широкое применение. С помощью тонких переходных элементов можно, например, решать задачи о посадках деталей машин и зазорах между ними. При использовании очень узкого переходного элемента между двумя частями конструкции или деталями машины зазоры учитываются введением такой начальной деформации Ву-о, что величина teyo равняется величине зазора. Поскольку описанный переходный элемент не передает растяжения, быстро получаем ответ на вопрос, закрывается ли зазор. И наоборот, посадка эквивалентна отрицательной начальной деформации по нормали к переходному элементу.
Недостатком такой аппроксимации является необходимость использования переходных элементов конечной толщины, чтобы избежать появления очень больших коэффициентов жесткости в направлении нормали и, следовательно, плохо обусловленных уравнений. Для того чтобы обойти упомянутые затруднения, можно использовать другие методы, имеющие более специальное назначение [29].
18.7. Ползучесть: деформации, зависящие от времени 18.7.1. Общие положения
Явления ползучести характеризуются зависимостью деформации не только от напряжения, но и от времени. Деформации в данный момент времени определяются всей предысторией напряженного состояния. Таким образом, любой вычислительный процесс должен сводиться к расчету приращений для достаточно малых отрезков времени. Для каждого такого отрезка времени, используя заданный закон ползучести, средние для этого отрезка напряжения и при необходимости их предыдущие значения, можно определить приращения деформаций. Таким образом, в рассматриваемом случае естественно использовать описанный в подразд. 18.2.4 метод начальных деформаций.
Однако иногда можно обратить закон ползучести и получить закон, по которому напряжения в любой момент времени опре-
деляются предысторией деформирования. В тех случаях, когда удобно использовать функцию релаксации, можно применять описанный в подразд. 18.2.3 метод начальных напряжений.
Поскольку при ползучести удобнее измерять деформации, обычно рекомендуется применять метод начальных деформаций, который и будет использован в дальнейшем.
При применении метода начальных деформаций к задачам теории ползучести обычно [30-34]:
а) рассматриваются все изменения нагрузки (температуры и т. д.) в начальный момент t некоторого отрезка времени и определяется напряженно-деформированное состояние из решения задачи теории упругости;
б) определяется изменение деформации ползучести {Две}; за рассматриваемый отрезок времени в предположении, что при этом полученное -на этапе а напряженное состояние не меняется;
1з) величина {Aec}i используется как начальная деформация и в результате решения задачи теории упругости определяется новое напряженно-деформированное состояние в конце рассматриваемого отрезка времени.
Если отрезок времени At достаточно мал, то описанный процесс отражает истинное поведение материала и можно перейти к расчетам для следующего отрезка времени. .Если изменения деформаций относительно велики, то можно повторить этапы б и в , используя для определения {Дес}( уточненные средние значения напряжений. Осуществление таких итераций иногда желательно, но редко требуется более двух циклов.
Ясно, что устойчивость описанного процесса зависит от выбранной величины отрезков времени и для каждой задачи необходимо ее проверять.
Здесь уместно сделать одно замечание относительно эффективности вычислений. Если упругие мгновенные свойства материала не изменяются во времени (и на них не влияет изменение во времени температуры), то очевидно, что многократно будет применяться один и тот же метод нахождения упругого решения. В таких случаях удобнее хотя бы частично обращать .матрицы, встречающиеся при решении, чем использовать итерационные методы решения, И наоборот, если упругие свойства меняются во времени и на каждом отрезке времени приходится решать существенно различные задачи теории упругости, то целесообразнее использовать итерационные методы решения, принимая за начальное приближение полученные ранее значения перемещений.
Основной проблемой, возникающей при использовании описанного метода, является построение алгоритма определения
приращения деформации {Две}. Она рассматривается в последующих разделах.
18.7.2. Ползучесть, зависящая от предыстории деформирования (вязкоупругость )
Явления вязкоупругости характеризуются тем, что скорость деформации ползучести зависит не только от мгновенного напряженно-деформированного состояния, но и от всей его предыстории. Таким образом, для определения приращения деформации {ДвсЬ на каком-либо отрезке времени надо знать напряжения н деформации во все предыдущие моменты времени. Поскольку в процессе рещения задачи они вычисляются, в принципе затруднений не возникает. Однако даже самые большие ЭВМ не в состоянии хранить всю историю в оперативной памяти, а многократное использование дополнительных запоминающих устройств требует много времени. Поэтому использование этого метода экономически невыгодно.
Метод, описанный Зенкевичем и др. [31] для задач линейной вязкоупругости, позволяет обойти эту трудность. Его можно обобщить и на случай решения задач нелинейной вязкоупругости.
В линейной теории вязкоупругости соотношение между напряжениями и деформациями всегда можно записать в форме, сходной с используемой в теории упругости, например в виде (18.2), заменяя упругие постоянные в матрице [D] соответствующими дифференцнальны.чн нлн интегральными операторами [35]. Для изотропного материала вместо двух упругих постоянных можно использовать два оператора, а для анизотропных-мате-. риалов может потребоваться 21 оператор.
Таким образом, деформация ползучести может быть описана соотношением вида
{8,} = [D]-W,
где каждый элемент матрицы вязкоупругости [Л]- прн исполь-зованнн дифференциальных операторов имеет внд
Й - ao + ax{dldt) + a,(dldP) + ... ns 47
bo + bj{dldt) + bAdydt) +...
Если эти разложения конечны, то, выделяя мгновенные упругие эффекты, соотношение (18.37) можно представить в виде суммы элементарных дробей
+ ./Лр + (18.38)
d/dt + Bi
didt -Ь Bj
Как известно, эта сумма характеризует поведение показанного на фиг. 18.14 набора элементов Кельвина (хотя физически
использование таких моделей может и не иметь смысла). Каждый член суммы характериз.ует один элемент Кельвина. Типичный вклад в компоненту деформации представляет собой, таким образом, слагаемое вида
--- (18.39)
или
d/dt + Вп
(ел-) = Лл-бА-
(18.40)
Записанное выше соотношение позволяет определить приращение каждого такого слагаемого за какой-либо отрезок времени,
Фиг. 18.14. Набор элементов Кельвина.
если известны текущее значение компоненты напряжения о, и текущее значение е„. Таким образом, для описания процесса необходимо хранить только конечное число текущих значений е„ ).
На практике для описания поведения материала используется ограниченное число элементов Кельвина и небольшое число вязкоупругих операторов. Например, для изотропного несжимаемого материала матрица [D] определяется только одним оператором. Если этот оператор представляется двумя слагаемыми суммы (18.38), то в процессе вычислений требуется хранить лишь две величины [31]).
Вычислительный процесс не усложняется если величины А„ и В„ для каждого элемента Кельвина зависят от 1зременн и температуры, что характерно для задач термовязкоупругости (например, задач о ползучести бетона илн пластмасс).
Задавая зависимость постоянных пружины н поршня Л и S от текущих напряжений, можно обобщить метод на нелинейные
) В более поздних работах они получили название переменных состояния,
) Для произвольного линейного вязкоупругого оператора метод экономии оперативной памяти при численном счете указан в работе Б, Е, Победри Численные методы в теории вязкоупругости , .Механика полимеров, Ns 6, 1973.- Прим. ред.
вязкоупругие явления. Вопрос о формулировке таких законов, согласующихся с экспериментальными результатами, еще не решен окончательно.
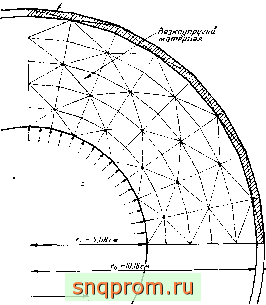
Для иллюстрации применения описанного метода возьмем пример из работы [31]. Это задача о расчете скрепленного с металлической оболочкой цилиндра нз вязкоупругого материала. Так как задача, по существу, одномерная, имеется точное решение [36]. Использовалась программа расчета двумерного состояния. Для получения решения, соответствующего t = 10, понадобилось 100 шагов прн шаге по времени, равном 0,1 (фнг. 18.15 и 18.16). В работе [31] приведены и другие более сложные примеры.
18.7.3. Законы теории ползучести, учитывающие зависимость от напряженно-деформированноео состояния
Хотя, несомненно, вся предыстория напряженно-деформированного состояния влияет на ползучесть большинства материа-
, Сталь
.0.31см
Фиг, 18 15. Решение задачи о нагруженном внутренним давлением подкрепленном вязкоупругом цилиндре как двумерной задачи.

1 =5,0 ( = 3,0
г = 1.0
( = 0,5
= О
05 0,4 0,3 0.1 0.1 О
-0,1 -0,2 -0,3 -ОД
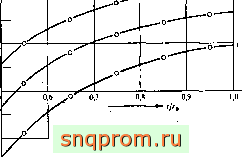
Фиг. 18.16. Изменение во времени тангенциального напряжения в цилиндре, показанном на фнг. 18.15.
Материал подкрепления уаругяй. Сдвиговые свойства внутреннего цилиндра вязкоупругие, а объемные -упругяе 131,36].. Результаты совпадают с точными [36[.
лов, сильно нелинейная зависимость от напряжений, характерная почти для всех металлов, позволяет записать законы в упрощенной форме, которая дает возможность оценить скорость деформации по текущим значениям переменных состояния (в частности, напряжения, деформации, времени н температуры).
Обзор таких законов сделан в работе [37], Деформацию ползучести изотропного несжимаемого материала можно, например.
определить выражением
1 (t) Рг (ёс) FAd)J\{b) [0 Г' [о]
d f 1
(18.41)
где матрица [io] эквивалентна соответствующей матрице упругости с коэффициентом Пуассона, равным 0,5; ё^, ст-вторые
инварианты деформации ползучести и напряжения и 6 -температура.
При вторичной ползучести зависимость от времени накопленной деформации слабая и часто используется степенной закон [38, 39]
ZfWc--Ё
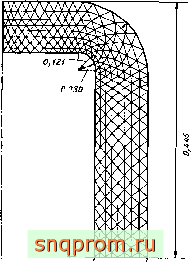
Фиг. 18.17. Расчетная схема сосуда высокого давления с плоским днищем [33]. Внутрениее давление 3 - [0 Н м^; модуль Юнга 1,35 10 Н,м^ коэффициент Пуассона 0,3,
.(18.42)
Хотя физические аргументы в пользу таких теорий спорны, особенно относительно явной зависимости от времени, описывающей так называемое старение,их очень просто использовать в практических приложениях. Определение скорости деформации ползучести
в любой момент времени не представляет труда, и, следовательно, приращение деформации ползучести может быть найдено просто как
Д{8Ь = {еЬД/. (18.43)
Это выражение непосредственно используется в процессе вычислений.
С приложениями метода можно познакомиться по работам [33, 34 и 40]. На фиг. 18.17 и 18.18 показаны некоторые примеры из работы [33].
В подобных и других задачах ползучести важно достичь наилучшего компромисса между требованиями экономичности И
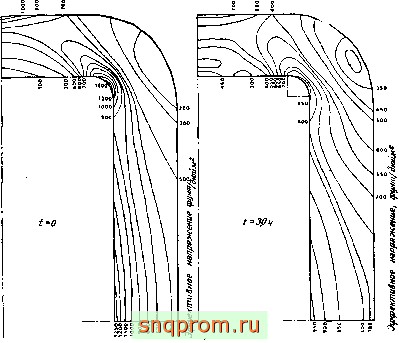
Фиг. 18.18. Измеиеппе во времени эффективного (октаэдрнческого) напряжения после приложения внутреннего давления [33].
устойчивости решения. Так, интервалы времени следует, как правило, выбирать в процессе вычислений. Они могут значительно увеличиваться, если, как это часто бывает, распределение напряжений приближается к установившемуся. Подходящим критерием выбора может служить требование, чтобы относительные приращения напряжений за рассматриваемый отрезок времени не превышали заданной величины [34].
18.8. Некоторые специальные приемы решения задач ползучести
Довольно часто с помощью некоторых обобщений или упрощающих предположений удается получить достаточно точные решения, учитывающие эффект ползучести, не прибегая к трудоемким и дооогостоящим методам приращений. .
Линейная вязкоупругость. Для однородных изотропных вяз-коупругнх материалов с постоянным оператором коэффициента Пуассона, используя аналогии Алфрея - Мак-Генри и решая задачу теории упругости при соответствующих эквивалентных нагрузках, перемещениях н температурах, можно определить напряжения и перемещения в любой заданный момент времени [41J.
Некоторые обобщения этих аналогий предложены Хилтоном [42].
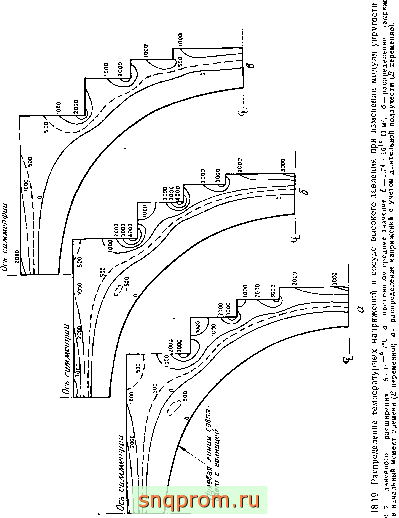
Кроме того, если деформация ползучести стремится к некоторой постоянной величине при / -♦ оо, то окончательное распределение напряжений можно найти и тогда, когда упомянутые аналогии нельзя применить. Например, если на конструкцию из вязкоупругого материала, свойства которого зависят от температуры, действуют не изменяющиеся во времени нагрузки и температура, то можно Определить предельные упругие постоянные и свести задачу к линейной задаче теории упругости для неоднородного материала [43]. Влияние такого изменения упругих свойств на распределение температурных напряжений в реакторе высокого давления показано на фиг. 18.19.
Установившаяся ползучесть. Если при ползучести, описываемой соотношением (18.42), полные деформации ползучести настолько велики, что упругими деформациями можно пренебречь, то удается получить существенные упрощения. В этом случае скорости полной деформации н деформации ползучести одинаковы и определяющие уравнения можно записать в виде
4{в} = {вЬ = №Г>1, (18.44)
как для изотропного несжимаемого материала.
Если соотношения между перемещениями н деформациями (или уравнения совместности деформаций) продифференцировать по времени, то станет ясно, что задача представляет собой задачу нелинейной теории упругости, в которой обычные деформации и перемещения заменены на скорости деформаций и скорости. Решение для этих величин не зависит от времени и его можно получить любым из описанных ранее методов, не прибегая к методам приращений. При этом напряженное состояние конструкции постоянно, а деформации возрастают пропорционально времени.
18.9. Заключительные замечания
В предыдущих разделах рассмотрены общие методы решения задач при использовании сложных нелинейных определяющих уравнений и некоторые частные приложения. Ясно, что этот
 1
1 ...
18 19 20 [
21 ]
22 23 24 ...
27

