Главная страница сайта  Российские промышленные издания (узловые агрегаты) 

1 ... 17 18 19 [ 20 ] 21 22 23 ... 27

Матрица [А] характеризует геометрические соотношения между ускорениями узлов и величиной О (если направление U совпадает с направлением одной из координат, то она состоит из единиц и нулей).

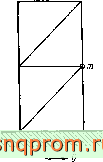
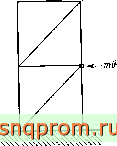
Неподвижное основание Фиг 17.9. Эквивалентность движения основания действию силы.

Типичное дифференциальное уравнение можно записать в виде

-а,5г; + 2а>.с,--г;-Ь^г;=С/(а (17.34)

где

Ri = [b,}\[M]{A}. (17.35) Решение уравнения (17.34) имеет простой внд

z- = \iJ(t)t

-CO; ((-Т)

sin (s>i (t - t) dx

(17.36)

H его можно вычислить для любых типов движения.

При расчете конкретных конструкций необходимо знать весовые множители вычисление которых можно предусмотреть в программе решения задачи о собственных значениях.

С помощью уравнения (17.34) рассчитывались реакции системы с одной степенью свободы на воздействия сейсмического характера. Часто можно видеть, что поведение системы определяется небольшим числом собственных функций и что для определения максимальной реакции достаточно сложить максимальные реакции, соответствующие этим собственным функциям,

ЛИТЕРАТУРА

Ь

За. ЗЬ.

9. 10.

12. 13.

14. 15.

16. 17. 18. 19. 20.

Crandall S. Н., Engineering Analysis, McGraw-Hill, 1956.

Wilkinson J. H., Tlie Algebraic Eigenvalue Problem, Oxford Univ. Press,

1965.

Cox H. L., Vibration of Missiles, Aircraft Eng., 33, 2-7, 48-55 (1961). Jenning A., Natural Vibration of a Free Structure, Aircraft Eng., 34, 81-83 (1962).

Irons в.. Eigenvalue Economisers in Vibration Problems, /. Roy. Aero. Soc, 67, 526 (1963).

Irons в.. Structural Eignevalue Problems: Elimination of Unwanted Variables, JAIAA, 3, 961 (1965); есть русский перевод: Айронс, Задачи cr Собственных значениях матриц конструкции: исключение лишних переменных. Ракетная техника и космонавтика, 3, № 5, стр. 207 (1965). Guyan R. J., Reduction of Stiffness and Mass Matrices, JAIAA, 3, 380 (1965); есть русский перевод: Гайан, Приведение матриц жесткости и массы. Ракетная техника и космонавтика, 3, № 2, стр. 287 (1965). Anderson R. G., Irons В. М., Zienkiewicz О. С, Vibration and Stability of Plates Using Finite Elements, Int. J. Sotids and Struct., 4, 1031-1055 (1968). Ramsden J. N., Stoker J. R., Mass Condensation; a Semi Automatic Method for Reducing the Size of Vibration Problems, Int. J. Num. Meth. Eng., 1, 333-349 (1969).

Barton M. v.. Vibration of Rectangular and Skew Cantilever Plates, /. Appl. Mech., 18, 129-134 (1951).

Clough R. W., Chopra A. K., Earthquake Stress Analysis in Earth Dams, Structures and Materials Research Rept. № 65-8, Univ. of California, Berkeley, California, 1965.

Ahmad S., Anderson R. G., Zienkiewicz O, C, Vibration of Thick, Curved, Shells with Particular Reference to Turbine Blades, /. Strain Analysis, 5, 200-206 (1970).

Anderson R. G., A Finite Element Eigenvalue System, Ph. D. Thesis, Univ. of Wales, Swansea. 1968.

Archer J. S., Rubin C. P., Improved Linear Axi-Symmetric Shell-Fluid Model for Launch Vehicle Longitudinal Response Analysis, Proc. Conf. on Matrix Methods in Struct. Mech., Air Force Inst, of Techn., Wright Patterson A. F. Base, Ohio, 1965.

Argyris J H., Continua and Discontinua, Proc. Conf. on Matrix Methods in Struct. Mech., Air Force Insl. of Techn., Wright Patterson A. F. Base, Ohio, Oct. 1965.

Klein S., Sylvester R. J., The Linear Elastic Dynamic Analysis of Shells of Revolution by the Matrix Displacement Method, Proc. Conf. on Matrix Methods in Struct. Mech., Air Force Inst, of Techn., Wright Patterson A F. Base, Ohio, Oct. 1965.

Dungar R., Severn R. Т., Taylor P. R., Vibration of Plate and Shell Structures Using Triangular Finite Elements, /. of Strain Analysis, 2, 73-83 (1967).

Arlett P. L., Bahrani A. K., Zienkiewicz O. C, Application of Finite Elements to the Solution of Helmholtzs Equation, Proc. lEE, 115, 1762-1964 (1968).

Taylor С Patil B. S., Zienkiewicz O. C, Harbour Oscillation: a Numerical Treatment for Undamped Natural Modes, Proc. Inst. Civ. Eng., 43, 141-

1969).

Zienkiewicz O. C, Irons В., Nath В., Natural Frequencies of Complex, Free or Submerged Structures, by the Finite Element Method, Symp. on Vibrations in Civil Eng., Inst. Civ. Eng., London (Butterworth), 1965. Back P. A. A., Gassell A. C, Dungar R, Gaukroger D. R., Severn R. Т., The Seismic Design Study ot a Double Curvature Arch Dam, Proc. Inst. Civ. Eng., 43, 217-248 (1969).

21. Zienkiewicz О. С, Newton R, Е„ Coupled Vibrations of a Structure Submerged in a Compressible Fluid, Int. Symp, on Finite Element Techniques, Stuttgart, 1969.

22. Holbeche J Ph. D, Thesis, Univ. of Wales, Swansea, 1971,.

23. Irons B, M., Role of Part-Inversion in Fluid Structure Problems with Mixed Variables, JAIAA, 7, 568 (1970); есть русский перевод; Айроис, Роль частичного обращения в задачах со смешанными переменными о поведении системы жидкость - конструкция, Ракетная техника и космонавтика, 8, № 3, стр. 239 (1970).

24. Housner G. W Behaviour of Structures During Earthquakes, Proc. Am. Soc. CiB. En 85, EM4, 110-129 (1959),

25 Zienkiewicz O. C, Anderson R, G Irons В., Buttress Dam Analysis for Earthquake Loads, Water Power, 19, 359-363 (1967),

18.1. Введение

Все рассмотренные до сих пор задачи описывались линейными дифференциальными уравнениями, приводящими к стандартной квадратичной форме функционала. В задачах механики упругого тела линейность являлась следствием:

а) линейной связи между деформациями и перемещениями [см. соотнощение (2.2)];

б) линейной связи между напряжениями и деформациями [см. соотношение (2,3)].

В задачах теории поля такая линейность была следствием предположения о независимости постоянных, например проницаемости к, от искомого потенциала ф [см. соотношение (15.1)].

Однако многие практически важные задачи не являются линейными, поэтому обобщение изложенных численных методов, которое позволило бы исследовать такие задачи, представляет большой интерес. В механике твердого тела такие явления, как пластичность, ползучесть и другие сложные реологические явления, заставляют отказаться от предположений линейной упругости. Аналогично ситуации, когда вязкость зависит от скорости потока или когда в пористых средах неприменимы законы фильтрации Дарен из-за наличия турбулентности или магнитная про-1Шцаемость зависит от плотности тока, приводят к физической нелинейности

Эти задачи можно исследовать, не меняя их постановки, т. е. на основе тех же основных вариационных принципов. Если найдено решение линейной задачи, то можно получить решение нелинейной задачи с помощью некоторого итерационного процесса, на каждом шаге которого материальные константы выбираются так, чтобы удовлетворялись определяющие уравнения.

Однако если нелинейна связь между деформациями и перемещениями, то необходимы более существенные изменения в постановке задачи. Такие задачи в настоящей главе не рассматриваются (они изложены в гл. 19). Тем не менее будет установлено, что итерационные методы применимы и для этого случая, поэтому с их помощью можно решать задачи, в которых имеют место нелинейности обоих типов ).

) То есть физическая и геометрическая, - Прим. ред.

ФИЗИЧЕСКИ НЕЛИНЕЙНЫЕ ЗАДАЧИ. ПЛАСТИЧНОСТЬ, ПОЛЗУЧЕСТЬ ЗАДАЧИ НЕЛИНЕЙНОЙ ТЕОРИИ ПОЛЯ И Т. Д.

Следует сделать одно существенное замечание. В нелинейных задачах в отличие от линейных часто нет единственности рещения. Таким образом, найденное решение не обязательно будет искомым. Для получения правильного ответа необходимо применять метод малых приращений и четко представлять физическую сущность задачи.

Здесь могут быть использованы формальные численные итерационные методы, такие, например, как методы Ньютона - Рафсона и т. д. Однако их применение требует понимания физической природы задачи, и поэтому на практике численные методы более успещно разрабатываются инженером (или физиком), нежели математиком.

НЕЛИНЕЙНЫЕ ЗАДАЧИ МЕХАНИКИ ТВЕРДОГО ДЕФОРМИРУЕМОГО ТЕЛА

18.2. Подход с общих позиций

18.2.1. Основные положения

Задача линейной теории упругости в перемещениях всегда сводится к решению уравнений для ансамбля (см. гл. 1 и 2)

[К] {5}-{i?} = 0,

(18,1)

где вектор {R} содержит все силы, обусловленные внешними нагрузками, начальными напряжениями и деформациями и т. д.

При выводе этого соотношения использовался закон линейной упругости в виде

{a} = [Dl({e}-{eo}) + {ao}. (18.2)

Кроме того, предполагалось существование линейной связи между деформациями и перемещениями [соотношение (2.2) гл. 2], перемещения считались непрерывными и уравнения равновесия удовлетворялись приближенно.

При решении задач о малых деформациях, в которых используются другие, возможно и нелинейные, определяющие уравнения, следует изменить только соотношение (18.2). Новое соотношение можно записать в виде

F{{a}, {е}) = 0.

(18.3)

Если удастся найти такое решение уравнения (18:1), что при соответствующем подборе одного или нескольких входящих в {18.2) параметров [D], {ео} или {оо} это уравнение и соотношение (18.3) удовлетворяются при одинаковых значениях напрят жений и деформаций, то полученное решение 6ijdeT искомым.

Очевидно, что при решении целесообразно использовать итерационный метод. Какая из трех вышеупомянутых величин будет подбираться в процессе итераций, зависит от:

а) метода решения линейной задачи;

б) физического закона связи между напряжениями и дефор -мациями.

Если при итерациях подбирается матрица [D], то приходим к известному методу переменной жесткости^). Если же подбираются {ео} или {оо}, то имеем так называемые методы начальных деформаций или начальных напряжений.

Во многих случаях не удается установить соотношения типа (18.3) для полных деформаций и напряжений, но можно вывести их для приращений этих величин Л {а} и А {в}. В этих случаях итерационные методы применяются для каждого приращения нагрузки (или времени при ползучести). Методы приращений можно использовать в сочетании с любым из ранее рассмотренных методов.

Из изложенного ранее видно, что параметры [D], {во}, {оо} являются весьма важной частью исходных данных для программы решения задачи линейной теории упругости. Поэтому такие программы представляют собой основу решения любой нелинейной задачи. На данной стадии несущественно, составлены ли эти программы на основе конечно-элементной дискретизации или нет. Изложенные ниже методы можно использовать в сочетании с любым другим способом дискретизации (например, конечно-разностным) при условии, что берутся одинаковые исходные данные.

18.2.2. Методы переменной жесткости

Метод переменной жесткости можно использовать в случае, когда связь между напряжениями и деформациями (18.3), характеризующую поведение материала, можно представить в форме (18.2), где матрица упругости зависит от достигнутого уровня деформации, т. е. имеет вид

[D]=[D({e})]=[D({6})], (18.4)

Так как матрица упругости влияет на окончательный вид матрицы жесткости ансамбля, приходим к уравнению

W = [/С ({б})] {6}= О, (18.5)

которое можно решить различными итерационными методами.

) В советской литературе этот метод носнт название метода переменных параметров. О других методах см. сб. Упругость н пеупругость , вып. 3, -стр. 120, Изд-во МГУ, \т.~При.м. ред.

Очевиден следующий простой итерационный процесс. Сначала предполагается {б}о = О, вычисляется [С({б}о)] = [о] и определяется {6}i = [XohW Процесс повторяется в соответствии с формулой

(18.6)

до тех пор, пока перемещения перестанут изменяться.

Если определяющие уравнения таковы, что соотношение типа (18.4) может быть записано только для приращений напряжений и деформаций, то описанный процесс следует применить Для приращений нагрузки, отсчитываемых от ранее достигнутого значения.

В любом случае можно пользоваться стандартной программой решения задач линейной теории упругости при условии,-что матрица [D] симметрична. Это требование весьма существенно, так как в программе обычно используется свойство симметрии.

Одним из существенных недостатков методов переменных параметров является то, что на каждом шаге приходится заново строить матрицы жесткости и решать полученные уравнения. Если программа использует прямые методы решения, то такой подход становится очень неэкономичным и более приемлемыми оказываются другие методы, которые описаны в следующем разделе.

18.2.3. Методы начальных напряжений

Если определяющие уравнения разрешимы относительно напряжений, т.е. (18.3) имеет вид

W = f({8}), (18.7)

то соотношение (18.2) для упругого материала можно привести к форме (18,7), задавая соответствующим образом {оо}. Так как {(То) влияет на силы {R], приходим к решению уравнения

№ = [Xo]W-i?{{6}) = 0. (18.8)

Итерационный процесс проводится следующим образом. Сначала находится

где {о} соответствует приложенным нагрузкам. Определяются напряжения {oo}i. необходимые для приведения упругого решения в соответствие с реальными напряжениями при достигнутых деформациях. Далее с учетом начального напряжения с помощью соотношения (2.13) находится [R}i и определяется

{6Л = 1КоГ' {R>} и т. д.

[г}Ш-[Rn}

(18.9)

Процесс продолжается до тех пор, пока решение не перестанет изменяться ).

Другой удобный метод состоит в определении только изменений [R}, обусловленных изменениями требуемого начального напряжения. В этом случае {бо} находится, как и ранее, но

A{S,} = [Co] AW} и т. д.

и итерации продолжаются до тех пор, пока величина А {б} не станет достаточно близкой к нулю.

При вычислениях более удобен последний подход, который, кроме того, имеет ясный физический смысл. На каждом этапе во всех точках конструкций определяется разность между истинными напряжениями при соответствуюи^их деформациях и напряжениями, найденными из упругого решения. Эта разность напряжений затем перераспределяется в соответствии с упругим законом, чтобы восстановить равновесие, и поэтому метод первоначально получил название метода перераспределения напряжений [1].

Величину силы А {/?}

п, Вычисленную на п-ы шаге итерации, можно физически интерпретировать как неуравновешенную невязку силы в конструкции, и, следовательно, она является удобной мерой ошибки.

В этом методе на каждом шаге итерационного процесса используется одна и та же матрица жесткости, и если она поблочно обратима, то время, необходимое для каждой итерации, составляет лишь небольшую часть времени, затрачиваемого на получение первого приближения.

Теперь вoзqкaeт вопрос, какие упругие постоянные следует использовать для определения матрицы [Ко]. Если поведение материала в основном описывается соотношениями линейной теории упругости и отклонения от линейно-упругого поведения локализованы, то естественно использовать начальные значения упругих постоянных. Однако если нелинейность проявляется для всех напряжений, то для ускорения сходимости можно рекомендовать скорректировать упругие постоянные после первой итерации.

18.2.4. Методы начальных деформаций

В некоторых задачах, особенно в задачах ползучести, действующие напряжения нельзя выразить в явном виде через де-

) Описанный метод носит название метода упругих решений. См. А, А, И.тьюшин, Пластичность, ГИТТЛ, 1948, - Прим. ред.

формации. С другой стороны, в этих случаях можно определить деформации (или приращения деформаций) через напряжения, т. е. установить соотнощение типа

{e} = f({a}). (18.10)

Совпадение соотношений (18.10) и (18.2) может быть достигнуто при соответствующем выборе {ео}. Уравнение (18.8) опять решается итерационным методом, но теперь упругие деформации, получаемые на каждом шаге, сравниваются с деформациями, соответствующими определяющему соотношению (18.10),

е

Фиг. 18.1. Методы начальных деформаций и начальных напряжений. Размягчающийся (а) и затвердевающий (б) материалы.

и НХ разность используется для оценки невязки силы А{} . В остальном процесс идентичен описанному выше, и, в частности, матрица жесткости остается постоянной на любом шаге.

В некоторых законах ползучести (см. разд. 18.7) дополнительные деформации (деформации ползучести) явно отделены от упругих деформаций и, следовательно, при каждой итерации определяются непосредственно дополнительные начальные деформации. Различие между методами начальных напряжений и начальных деформаций лучше всего, вероятно, проиллюстрировать графически. На фиг. 18.1 уровню напряженно-деформированного состояния, полученному в первом приближении, соответствует точка 1. В методе начальных напряжений полученные напряжения уменьшаются до правильного значения введением некоторого начального напряжения A{oo}i, тогда как в методе

начальных деформаций значения деформаций корректируются поправочным членом Л{ео}. Ясно, что когда с ростом напряжений деформации быстро увеличиваются, предпочтительнее использовать первый метод, а когда справедливо обратное утверждение (затвердевающие материалы) - второй.

18.2.5. Ускорение сходимости

Методами начальных напряжений и начальных деформаций можно получить окончательное решение, если правильно подобрать значения {оо} или {ео}. Однако описанные процессы подбора не всегда обладают быстрой сходимостью. Исследуя сходимость в процессе вычислений и вводя на каждом этапе дополнительные поправки, ее можно ускорить. Одна из таких процедур в общих чертах описана в работах [2а] и [26]. Однако инженер, составляющий програм.му, может проявить здесь свою изобретательность. Любой метод является вполне законным, если окончательное решение удовлетворяет всем требованиям.

18.3. Математический подход

На этой стадии важно пересмотреть всю проблему в целом с математических позиций [3].. Читатель, несомненно, знаком с методом Ньютона решения нелинейных уравнений с одной переменной X вида

ф{Аг) = 0.

Если приближенное решение х„ достаточно близко к точному, нО в то же время {х-п) Ф О, то его можно уточнить, полагая

где

Сходимость метода Ньютона графически показана на фиг. 18.2, а. Можно поступить по-другому и на каждом шаге использовать некоторое постоянное значение величины

тогда поправка принимает вид

Такой процесс, изображенный на фиг. 18.2, б, обычно сходится медленнее. Ясно, что эти же идеи легко обобщить на нелинейные уравнения со многими переменными. В этом случае процесс известен как метод Ньютона-Рафсона, который в свою очередь может быть модифицирован аналогично тому, как это сделано выще. Очевидно, что методы переменной и постоянной жесткости, рассмотренные с общих позиций в разд. 18.2, относятся к этим двум категориям.

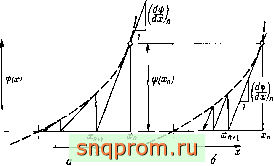
Фнг. 18.2. Итерационный метод Ньютона (а) н метод с нспользованнем постоянного наклона (б).

Для проведения дальнейщих выкладок удобно вернуться к основным уравнениям метода конечных элементов, полученным из принципа виртуальной работы в гл. 2. Уравнения (2,28) представляют собой уравнения равновесия, полученные из условия равенства изменений внутренней и внешней работ. Если {ф} представляет собой вектор суммы внутренних и внешних сил, то можно записать

d{6y{ii}=\d{ef{a}dV-d{bf{R} = Q, (18.11)

где вектор {R} содержит все внешние силы, обусловленные приложенными нагрузками. Если для вариации деформаций справедливо соотношение

d[e} = lB]d{6}, (18.12)

то, исключая {б}, получаем справедливое в общем случае соотношение

{t am = \ [BY {oi dV - {R} = 0, (18.13)

В котором {а} - истинные напряжения, зависящие от достигнутого уровня деформаций.

Если деформации малы, то [В] - зависящая от координат матрица деформаций, которая уже была определена ранее в гл. 2. Если можно установить зависимость {о} от деформаций и, следовательно, от перемещений, то задача сводится к решению нелинейного уравнения

г1)({6}) = 0.

На этом заканчивается постановка задачи.

Рассмотрим теперь вариацию (ij)} по d{6}, которая имеет вид

(18.14)

dW=\[BYd{o}dV,

так как {R} не зависит от {6} и d{R} = 0. Если записать

d[o}[Dr{{e})]d{e}, (18.15)

где [От]-матрица упругих постоянных для приращений (или касательных модулей), то, используя соотношение (18.15) вместе с (18.12), можно переписать (18.14) в виде

{Ф} = (S [BY [Dr ({е})1 [В] dV d {6} = [КА d {б}. (18.16)

Если теперь применить метод Ньютона-Рафсона, начиная с некоторого приближенного решения {б} , которое не обращает в нуль значения {г|)} , то можно получить соотношение для поправки к этому решению

A{6u,=-[/Cri:w .

18.17)

где 1Кт]п - матрица касательных упругих постоянных, определенная для перемещений и деформаций, соответствующих приближенному решению {б}.

Таким образом, основыв'аясь на методе Ньютона - Рафсона, получаем еще один метод решения нелинейных задач с использованием переменной жесткости. Он отличается от описанного в подразд. 18.2.2 тем, что здесь применяется не секущая, а касательная жесткость. Этот метод гораздо удобнее на практике, так как физические законы обычно формулируются с использо-вапием касательной жесткости.

Однако если вместо касательной матрицы использовать постоянную матрицу, соответствующую начальной упругой жесткости, то метод Ньютона - Рафсопа') (фиг. 18.2,6) становится

) Этот метод называется модифицированным методом Ньютона -Кач-торовнча. - Прим. ред.

тождественным ранее описанным методам начальных напряжений и начальных деформаций.

Итак, для методов, основанных на простых физических соображениях, имеется математическое обоснование'). Ясно, что при использовании модифицированного метода Ньютона - Канторовича потребуется большее число итераций, хотя в целом, как указывалось ранее, метод более экономичен, поскольку необходимо обращение только одной матрицы жесткости. Может оказаться, что оптимальный в экономическом отношении вариант получится при удачном сочетании обоих методов -постоянной и переменной жесткости.

Таким образом, существенным в каждом нелинейном методе является способ непосредственного вычисления вектора {ф}, характеризующего неуравновешенность сил.

Вектор {г|)}и можно рассматривать как неуравновешенную невязку сил. Таким образо.м, он играет важную роль в вычислительном процессе.

К описанным методам решения могут применяться любые процедуры ускорения сходимости.

18.4. Пластичность 18.4.1. Оби{ая теория

Этот частный вид отклонения от линейно-упругого поведения хорошо известен для металлов и подробно изучен с теоретических позиций [4-7]. По существу, пластичность характеризуется не зависящим от времени необратимым деформированием, начинающимся лишь по достижении некоторого напряжения, известного как предел текучести.

Поверхность текучести. Обычно постулируется и подтверждается экспериментально, что текучесть начинается только тогда, когда напряжения {а} удовлетворяют критерию текучести

(М, %) = 0, (18.18)

где X-параметр упрочнения. Условие текучести можно наглядно представить в виде поверхности в п-мер1юм пространстве напряжений, положение которой зависит от мгновенного значения параметра и (фиг, 18,3).

Закон пластического течения (ассоциированный закон). Мизес [4] первый предложил соотношение, связывающее приращения пластических деформаций с поверхностью текучести. Различными авторами [4, 5] были высказаны эвристические сообра-

) Метод начальных напряжений фактически совпадает с описанным здесь, если аппроксимировать [Кт] матрицей [Ко].

жения в пользу предложенного соотношения; в настоящее время общепринятой, по-виднмому, является следующая гипотеза: если d{e}p - приращение пластической деформации, то

или для любой компоненты п

de . = X

дР дОп

Здесь 7, - неопределенный коэффициент пропорциональности. Это соотношение известно как ассоциированный закон и его можно трактовать как требование ортогональности вектора приращений пластических деформаций поверхности текучести в л-мериом пространстве напряжений.

Соотношения между полными напряжениями и деформациями. Предположим, что -изменение деформации при бесконечно малом приращении напряжения может быть представлено в виде суммы упругой и пластической частей, т. е.

d{8} = d{eb + d{eb.

(18.20)

Упругие приращения деформации связаны с приращениями напряжения, как обычно, симметричной матрицей [D]. Таким образом, соотношение (18.20) можно записать в виде

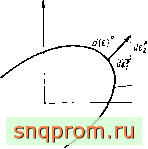
Г(б,.бгх)

%(е,}

Фиг. 18,3, Поверхность текучести и ассоциированный закон в двумерном пространстве напряжений.

d{z) = [Drd{a)+-K.

(18.21)

При пластическом течении напряжения находятся на поверхности текучести, определяемой равенством (18.18). Дифференцируя его, получаем

или

где введено обозначение

d {а} -АХ = 0,

(18.22)

(18.23)

Соотношения (18.21) и (18.22) можно записать в симметричной матричной форме

i dF

dF dF

da, da.

.. -A

(18.24)

Неопределенную постоянную X можно исключить (избегая при этом умножения нлн деления иа величину А, которая в общем случае может равняться нулю). В результате получаем выражение, в явном виде определяющее изменения напряжений через изменения деформаций:

d{a} = [D]ld{E}. (18.25)

Здесь

-1 ! - МI 1Ш' !+ {w}i°i ШГ-

(18.26)

Место матрицы упругости [D], используемой в методе приращений, занимает упруго-пластическая матрица [0]ёр. Она симметрична и имеет смысл независимо от того, равна ли нулю величина А. Подробное описание теории пластичности в такой форме впервые дано в работах [8, 9].

Значение параметра А. Ясно, что в случае идеальной пластичности без упрочнения величина А равна нулю. При учете упрочнения необходимо рассмотреть сущность параметра (или параметров) и, определяющего смещение поверхности текучести.

В упрочняющемся материале и определяется как пластическая часть работы при пластическом деформировании, т. е.

rfx. = a,def+ a,def + ... ={aYd{e}. (18.27)

Используя закон течения (18.19), получаем

d7i = X{aY

д{о]

(18.28)

Очевидно, что X можно исключить из (18.23) и записать

Это выражение позволяет определить А при известной зависимости F от к.

Соотношения Праидтля - Рейсса. Для иллюстрации некоторых понятий рассмотрим частный случай поверхности текучести Мизеса. Она определяется соотношением

F = [I (а, - o,f + Y - of + 4 (аз - +

+ За + ЗоЗ + За] - а = О, (18.30)

где в общем случае трехмерного напряженного состояния индексы 1, 2, 3 относятся к нормальным компонентам напряжений, а 4, 5, 6 - к сдвиговым. Из (18.30) находим

дГ 3oj

i

acr, ~ 2о dF 3g4 dOi, а

dF 3(7.2

dcTj 26- дзз OF 3cj6 dF

2a

5(75

дав

Штрихами обозначены компоненты девнатора тензора напряжений, т. е.

а; = а,-*+° + ° и т. д.

Величина а=ст(и)-одноосное напряжение при течении. Если известны результаты опыта для одноосного растяжения в виде зависимости а от пластической деформации Вир, то можно записать

d% = a ds p

и

да J а

где Н' - тангенс угла наклона кривой в точке, соответствующей а.

Подставляя это выражение в (18.29), после некоторых преобразований получаем

А = Н', (18.31)

что приводит к хорошо известным соотношениям Праидтля - Рейсса между напряжениями и деформациями.

С обобщением на случай поверхности текучести с угловыми точками можно познакомиться в работе [6].

18.4.2. Исторические замечания

Поскольку в изложенной теории пластичности законы сформулированы в виде соотношений (18.25) и (18.26) для приращений, ясно, что итерационный процесс необходимо применять

ДЛЯ малых приращений нагрузок. При этом можно использовать Любой из процессов, описанных в разд. 18.2.

В самых первых приложениях метода конечных элементов к задачам теории пластичности предпочтение отдавалось методам начальных деформаций (см., например, работы [10] и [И]). Однако эти методы совершенно неприменимы при рассмотрении идеальной пластичности (без упрочнения), поскольку в этом случае деформации при заданных напряжениях нельзя определить однозначно. По этой причине в последующих работах повысился интерес к методу переменной жесткости [12-16]. Некоторая экономия достигалась за счет того, что для решения систем уравнений использовался метод итераций и жесткость менялась в общем итерационном процессе.

Метод начальных напряжений, впервые примененный для-задач теории пластичности Зенкевичем и др. [9], по-видимому, наиболее удобен, так как любая разгрузка автоматически происходит по законам теории упругости, что позволяет исследовать циклическое нагружение. В настоящее время этот метод используется довольно широко [17].

18.4,3. Приложения метода начальных напряжений к некоторым задачам пластичности

Приспособить метод начальных напряжений к решению задач пластичности довольно просто. Трудности, возникающие при этом, связаны со следующими двумя обстоятельствами:

а) Соотношение между приращениями напряжений и деформаций (18.25) справедливо лишь с момента достижения напряжениями поверхности текучести, т. е. при F{a)=0. Если f (с)<0, то материал продолжает вести себя упруго.

б) Соотношение для приращений (18.25) справедливо лишь при бесконечно малом увеличении деформации. При увеличении на конечную величину напряжения могут выйти за пределы поверхности текучести.. Для предотвращения этого после каждой итерации надо изменять напряжения так, чтобы выполнялось условие текучести.

Метод, с помощью которого решены приведенные ниже примеры, состоит в следующем:

а) Для приращения нагрузки вычисляются приращения упругих напряжений и деформаций.

б) Для полученных полных напряжений вычисляется величина F{[a}). Если f <0, то поведение материала упруго и дополнительных итераций не требуется. Если F > О, то вычисляется значение F в начале интервала и путем интерполяцин

определяются приращения упругих деформаций и напряжений в окрестности точки на поверхности текучести.

С помощью соотношения (18.25) находится приращение упруго-пластического напряжения, соответствующее определенному таким образом упругому напряжению'). Напряжение в момент начала текучести после добавления упомянутого выше приращения сравнивается с определенными ранее полными напряжениями, а разность используется в качестве начального (поправочного) напряжения.

в) Далее вычисляют невязки сил и получают упругое решение, дающее новую величину полного напряжения. Если невязки сил меньше некоторого значения, то процесс заканчивается. В противном случае: г) повторяются этапы б и в и т. д.

На каждом этапе полные напряжения должны соответствовать поверхности текучести. Упруго-пластнческая матрица определяется по значениям напряжений, при которых F = О, или изменяется в процессе итераций.

Во всех приведенных примерах описанный итерационный процесс использовался без ускорения сходимости. При этом наблюдалась довольно быстрая сходимость (5-15 циклов). Медленная или плохая сходимость является обычно признаком критического состояния конструкции.

Полученная ранее упруго-пластическая матрица относится к общему случаю трехмерной сплошной среды. Для двумерных состояний необходимо привести ее к специальному виду. Например, для плоского напряженного состояния это достигается простым вычеркиванием в (18.24) столбцов, соответствующих нулевым компонентам напряжений. В случае плоской деформации должны учитываться все напряжения, но обращаются в нуль соответствующие компоненты деформаций. В работе [9] выполнены соответствующие преобразования и приведены явные выражения для матриц. Интересно отметить, что в этих случаях даже при идеальной пластичности диагональный член, соответствующий А, отличен от нуля.

Пластина с отверстием из упрочняющегося и неупрочняю-щегося материала. На фиг 18.4 показаны форма пластины и простые треугольные элементы. Получено решение задачи в предположении плоского напряженного состояния как для идеально пластического, так и для упрочняющегося материалов. Использовался критерий Мизеса с линейным упрочнением [по-

) Поскольку приращение нагрузки конечно, возможно, что определенные с помощью формулы (18.25) упругие напряжения будут несколько превышать предел текучести. Это проверяется, и в случае превышения предела текучести напряжения уменьшаются так, чтобы они находились на поверхности текуче сти.

среднее

Фиг. 18,4. Растяжение полосы с отверстием (плоское напряженное состояние).

а -разбиение на конечные элементы (149 элементов, 94 узла); б -пластические зоны для различных отношений Ccpei/ ;, идеальная пластичность, Я=6,85 . 10 Н/м', v==0.2, 0=2,38.108 Н/м'; е то же, что и на б, но для упрочняющегося материала. Постоянный наклон Н'1Е=й,йгг; г -нагрузка 0,98 приложена за один этап. Упрочняющийся материал.

стоянное Н' в (18.31)]. Зоны пластичности при различных нагрузках показаны на фиг. 18.4, бив.

Хотя соотношение пластичности справедливо только для приращений, метод начальных напряжений при приложении всех нагрузок за один этап приводит к решению, удовлетворяющему условиям равновесия и не превышающему напряжений текучести. Такое решение для очень большого приращения нагрузки показано на фиг. 18.4, г. Интересно отметить, что, несмотря на нарушение законов для приращений деформаций, пластические зоны практически не изменились.

U25 1.00

0.75 0.50 0,25

				.у

0 йд 15 Jo Is 3fi 45 0 4/5 £е/е.

Фиг. 18,5. Пластина с отверстием; упрочняющийся материал, Н'/Е = 0,032. Максимальная деформация в точке начала текучести. Приращение нагрузки = = 0,2 X ийгрузка, соответствующая-началу текучести.

- экспериментальные результаты Теокариса и Маркетоса 18]; О метод начальных

напряжений; X метод переменной жесткости 14]; Д решение для одного этапа нагружения в пластической области.

Важно также отметить, что, как видно из фип 18.5, максимальные деформации в точке начала текучести почти совпадают с определенным методом приращений. Там же проведено сравнение с экспериментальными результатами и с результатами, полученными методом переменной жесткости [14].

Консольная балка - циклическое нагружеиие. На фиг. 18.6 показана находящаяся в условиях плоского напряженного состояния консольная балка, для материала которой справедливы законы идеальной пластичности Мизеса. Нагрузки отнесены к критической нагрузке, определенной по элементарной теории пластического шарнира. На фиг. 18.7 показан первый цикл нагружения для иллюстрации способности метода правильно описывать упругое поведение при разгрузке. Заслуживают внима-

1 ... 17 18 19 [ 20 ] 21 22 23 ... 27