Главная страница сайта  Российские промышленные издания (узловые агрегаты) 

1 [ 2 ] 3 4 5 ... 27

Матрица [В] легко может быть получена из соотношения (2.1), если известны функции формы Л^(, Nj н Nm. В том случае, когда эти функции линейные, деформации постоянны по всему элементу.

2.2.3. Напряжения

В общем случае материал, находящийся внутри элемента, может иметь начальные деформации, обусловленные температурными воздействиями, усадкой, кристаллизацией и т. п. Если обозначить эти деформации через {ео}, то напряжения будут определяться разностью между существующими и начальными деформациями.

Кроме того, удобно предположить, что в рассматриваемый момент времени в теле существуют некоторые остаточные напряжения {оо}, которые, например, можно замерить, но нельзя предсказать без знания полной истории нагружения материала. Эти напряжения можно просто добавить к общему выражению. Таким образом, в предположении упругого поведения соотношения между напряжениями и деформациями будут линейными:

{0}==[D]({8}-{8o}) + {0o}, (2.3)

где [D] -матрица упругости, содержащая характеристики материала.

Для частного случая плоского напряженного состояния необходимо рассмотреть три компоненты напряжений, соответствующие введенным деформациям. В принятых обозначениях они записываются в виде

Матрица [D] легко получается из обычных соотношений между напряжениями и деформациями для изотропного материала [6]:

бд: - (ед:)о =-£ О^: --g- Oj

I \ I

ej, - (ej,)o = - -g- л: + -р tfj

Yxj,-(Yxj,)o =

2(1-fv)

V 1 0

1 -v

0 0

2 J

2.2.4. Эквивалентные узловые силы Пусть столбец

определяет узловые силы, которые статически эквивалентны граничным напряжениям и действующим на элемент распределенным нагрузкам. Каждая из сил {FJ должна иметь столько же компонент, сколько и соответствующее узловое перемещение {6i}, и действовать в соответствующем направлении.

Распределенные нагрузки {р} определяются как нагрузки, приходящиеся на единицу объема материала элемента и действующие в лаправлениях, соответствующих направлениям перемещений {f} в этой точке.

В частном случае плоского напряженного состояния узловые силы записываются в виде

где и и V-компоненты, соответствующие перемещениям и и V. Распределенная нагрузка имеет вид

где x и y-компоненты объемных сил .

Простейший способ сделать узловые силы статически эквивалентными действующим граничным напряжениям и распределенным нагрузкам состоит в задании произвольного (виртуального) узлового перемещения и приравнивании внешней и внутренней работ, совершаемых различными силами и напряжениями на этом перемещении.

Пусть d {S}-виртуальное перемещение в узле. С помощью соотношений (2.1) и (2.2) получим соответственно перемещения и деформации элемента в виде

d {!} = [N] d [ЪУ и d {е} = [В] d {6} (2.4)

Работа, совершаемая узловыми силами, равна сумме произведений компонент каждой силы на соответствующие перемещения, т. е. в матричном виде

(d {Ь}У . {F}. (2.5)

Аналогично внутренняя работа напряжений и распределенных сил, приходящаяся на единицу объема, равна

d{8}4cr}-d{f}4p} (2.6)

(d{6}T([Br{cr}-[N]4p}). (2.7)

Приравнивая работу внешних сил суммарной внутренней работе, получаемой интегрированием по объему элемента, имеем

(d {6}Т{РГ = (d {6}У (5 [B]{a}dV - 5 [Nf {p}dV). (2.8)

Так как это соотношение справедливо для любого виртуального перемещения, коэффициенты в правой и левой частях должны быть равны. После подстановки (2.2) и (2.3) получаем

{FY = {\т'[D] [В] dv) {6} - \ [BY [D] {во} dV +

+ 5[Bf K}dV-JiNf {p}dV. (2.9)

Эта зависимость является одной из основных характеристик любого элемента. В гл. I она приводилась в форме соотношения (1.3). Матрица жесткости принимает вид

(2.10)

Узловые силы, обусловленные распределенными нагрузками, имеют вид

{F} = -J[Nf (p}dV, (2.11)

а силы, обусловленные начальной деформацией, выражаются как

{F}; = -J[B]nD]{8o}dV. (2.12)

[kr=J [Bf[D][B]dV.

Узловые силы, соответствующие начальным напряжениям, записываются в виде

(п;=5[вгыс1У. (2.13)

Если система начальных напряжений самоуравновешена, то после составления ансамбля силы, определяемые соотношением

) Заметим, что в соответствии с правилами матричной алгебры транс [в'пЛ] произведения матриц осуществляется по формуле ([А\Щу =,

(2.13), тождественно равны нулю. Поэтому обычно оценка компонент этих сил не проводится. Однако если, например, часть изучаемой конструкции выполнена из .монолита, в котором существуют остаточные напряжения, или если исследуются выработки горной породы, в которой заданы тектонические напряжения, то необходимо учитывать, что удаление материала может вызвать нарушение силового баланса.

При использовании треугольного элемента в задачах о плоском напряженном состоянии основные характеристики получаются после соответствующей подстановки. Как уже было отмечено, в этом случае матрица [В] не зависит от координат и интегрирование выполняется тривиально.

Составление ансамбля и дальнейшее решение производятся с помощью простой процедуры, описанной в гл. I. В общем случае в узлах могут быть приложены сосредоточенные внешние силы. Тогда для сохранения равновесия в узлах следует дополнительно ввести матрицу сил

(R} =

(2.14)

Сделаем еще замечание по поводу элементов, соприкасающихся с границей. Если на границе заданы перемещения, то никаких затруднений не возникает. Рассмотрим, однако, случай, когда на границе задана распределенная внешняя нагрузка, скажем, нагрузка {g} на единицу площади. Тогда в узлах граничного элемента следует приложить дополнительную нагрузку. Это просто сделать, используя принцип виртуальной работы:

(2.15)

{F}; = -J[Nf{g}dS,

где интегрирование проводится по границе элемента. Заметим, что для того, чтобы записанное выше выражение было справедливо, {g} должно иметь такое же число компонент, как и {f}.

На фиг. 2.1 показан граничный элемент для случая плоского напряженного состояния. Интегрирование в (2.15) редко удается выполнить точно. Часто из физических соображений поверхностная нагрузка просто заменяется приложенными в- граничных узлах сосредоточенными силами, которые определяются из условий статического равновесия. Для рассматриваемого частного случая результаты будут эквивалентны.

После, того как из решения общей системы уравнений (типа встречающихся в строительной механике) определены узловые

2 Зак, 613

перемещения, из соотношений (2.2) и (2.3) могут быть найдены напряжения в любой точке элемента

{0} = [D] [В] {6}= - [D] {г,} + {0о}. (2.16)

В этом выражении нетрудно узнать типичные члены соотношения (1.4), причем матрица напряжений элемента имеет вид

[Sr=[D][B]. (2.17)

К этой матрице должны быть добавлены напряжения

K} = -[D]{M и {0о}. (2.18)

Отсутствие составляющей напряжения, вызванного распределенной нагрузкой {0}р, объясняется тем, что рассматриваются только условия общего равновесия, а не равновесия внутри каждого элемента.

2.2.5. Обобщенный характер перемещений, деформаций и напряжений

Физический смысл перемещений, деформаций и напряжений в рассмотренном случае плоского напряженного состояния был очевиден. Во многих других приложениях, приведенных ниже, эта же терминология может быть применена к другим физически менее наглядным величинам. Например, в рассматриваемом плоском элементе термин перемещение может обозначать прогиб и наклон в данной точке. Тогда деформациями будут кривизны срединной поверхности, а напряжениями - внутренние изгибающие моменты.

Все полученные здесь выражения справедливы и в общем случае при условии, что сумма произведений перемещений на соответствующие компоненты нагрузок определяет внешнюю работу, тогда как сумма произведений деформации на соответ- ствующие компоненты напряжений - внутреннюю работу.

2.3. Обобщение иа всю область.

Отказ от понятия внутренних узловых сил

В предыдущем разделе принцип виртуальной работы был Применен к отдельному элементу и введено понятие эквивалентной узловой силы. Для ансамбля в целом, очевидно, можно использовать подход, основанный непосредственно на представлении о равновесии.

Идею описания В13аимодействия элементов с помощью узловых сил математически трудно обосновать, хотя она очень привлекательна с точки зрения инженеров и допускает наглядную

интерпретацию. Тем не менее нет необходимости рассматривать каждый элемент в отдельности; рассуждения предыдущего разт дела можно непосредственно применить ко всему сплошному телу.

Можно считать, что соотношение (2.1) относится ко всей конструкции, т. е. что

{f} = [N]{6}, (2.19)

где столбец {6) содержит все узловые точки, а

N,= Nr.

(2.20)

если рассматриваемая точка принадлежит элементу е, т. е. точка i сопряжена с этим элементом. Если точка ( не принадлежит рассматриваемому элементу, то

N, = 0. (2.21)

Аналогично определяется матрица [В]. Затем принцип виртуальной работы может быть применен ко всей конструкции. Теперь нет необходимости рассматривать силы взаимодействия между элементами, и внешняя работа на виртуальных перемещениях d {6} всех узлов становится равной

d{6}4R}-Sd{f}4.p}dV-Jd{f}4g}dS, (2.22)

а внутренняя виртуальная работа принимает вид

Jd{8}-{0}dV,

(2.23)

где интеграл берется по всей области. После учетаУ

d{f} = [N]d{6}, d{e} = [B]d{6}, (2.24)

а также выражения (2.3) и приравнивания внутренней и внешней работ, получаем

[К] {6} + (F}p + {F}, + {F}, + {F} - {R} = 0. (2.25)

Произвольный элемент матрицы жесткости имеет вид

[K ] = S[B,][D][B,]dV, (2.26)

где интеграл берется по всей области.

Учитывая соотношение между [В]; и [В],-, имеем

(2.27)

где оценивается вклад каждого элемента, как это описано в предыдущем разделе.

Легко показать справедливость аналогичных выражений для различных компонент сил, входящих в уравнение (2.25).

Таким образом, при составлении ансамбля, как и ранее, мы не пользовались понятием межэлементных сил. В дальнейшем в этой главе индекс элемента е будем опускать, за исключением некоторых частных случаев. Кроме того, мы не будем делать различия между функциями формы для элемента и всей системы.

Необходимо обратить внимание на один важный момент. Рассматривая виртуальную работу системы в целом [выражение (2.23)] и приравнивая ее сумме работ каждого из элементов, мы тем самым предполагаем, что между элементами нет разрывов. Если такие разрывы возникают, то следует добавить работу напряжений в местах разрывов.

Таким образом, поле перемещений, определяемое функциями формы, должно быть таким, чтобы иа поверхностях разрыва деформации были ограниченными. Следовательно, для того чтобы общие уравнения были справедливы, перемещения должны быть непрерывными функциями. Об этом необходимом условии будет сказано ниже.

2.4. Метод перемещений как минимизация полной потенциальной энергии

Принцип виртуальных перемещений, использованный в предыдущих разделах, обеспечивает выполнение условий равновесия в определенных пределах, зависящих от выбранной формы перемещений. Равновесие будет полным только тогда, когда виртуальные работы равны при произвольных вариациях перемещений (удовлетворяющих только граничным условиям) ).

Если количество параметров {6}, описывающих перемещение, неограниченно возрастает, то условия равновесия могут быть удовлетворены.

Принцип виртуальной работы может быть сформулирован в различной форме. Приравнивая выражения (2.22) и (2.23), можно записать

\ d {еУ {а} dV - [d {ЬУН + \ d {ff {р} dV +

+ \d{fy{g}ds]=0. (2.28)

) Такие перемещения называются кинематически допустимыми. - Я/1 л.

Первый член в-этом уравнении соответствует вариации энергии деформации U конструкции, а второй - вариации потенциальной энергии W внешней нагрузки). Тогда вместо уравнения (2.28) имеем

d([/ + r) = rf(5c) = 0, (2.29)

где величина % называется полной потенциальной энергией. Это означает, что для обеспечения равновесия полная потенциальная энергия должна принимать стационарное значение. Система уравнений метода конечных элементов (2.25), полученная выше, является, по существу, отражением того, что варьирование перемещений осуществляется по конечному числу параметров {б}. Эта система может быть записана в виде

d&i

дх дЬг

= 0.

(2.30)

Можно показать, что для упругого материала полная потенциальная энергия не только стационарна, но и минимальна [7]. Таким образом, при использовании метода конечных элементов отыскивается минимум полной потенциальной энергии среди возможных перемещений заданной формы.

Чем больше степеней свободы имеет система, тем точнее будет приближенное решение, которое в пределе стремится к точному, соответствующему истинному равновесию. Таким образом, теперь можно сформулировать необходимые условия сходимости метода конечных элементов. Обсуждение этих условий перенесем, однако, в следующий раздел.

Интересно отметить, что если истинное равновесие требует абсолютного минимума полной потенциальной энергии то приближенное решение, полученное методом конечных элементов, будет давать всегда завышенное значение %. Таким образом, предельное значение полной потенциальной энергии всегда может быть оценено.

Если бы функция X была известна априори, то уравнения метода конечных элементов можно было бы получить непосредственным дифференцированием в соответствии с (2.30).

Подставляя в (2.28) определяющее уравнение теории упругости (2.3) и полагая, что нагрузки не зависят от перемещений.

) Если внешняя нагрузка обладает потенциалом, эти выражения могут рассматриваться как полные дифференциалы.

после интегрирования получаем

[i 5 [eVlD] {в} dV - \ UY [D] Ы dV +

+ \ {гУ [а,] dV] - [{б} {R} + J {fY {р} dV + \ {fY {g} ds] =

(2.31)

В этом соотношении выражение в первых квадратных скобках соответствует величине U, а во вторых - W. На практике выражение для полной потенциальной энергии обычно записывается сразу, что часто более удобно для метода конечных элементов. Читатель может убедиться в этом, если в качестве упражнения получит точные соотношения метода конечных элементов предыдущего раздела, исходя из уравнения (2.31) и дифференцируя по перемещениям, определяемым в соответствии с (2.19).

В хорошо известном приближенном методе Релея - Ритца [8, 9], часто применяемом для решения задач теории упругости, используется именно этот подход. Записывается выражение полной энергии и полагается, что форма перемещений зависит от конечного числа неизвестных параметров. Далее выводится система уравнений из условия минимума полной потенциальной энергии по этим параметрам. Таким образом, метод конечных элементов в изложенной постановке эквивалентен методу Релея-Ритца. Разница состоит только в способе задания перемещений. В методе Ритца они обычно задаются функциями, определенными на всей области и приводящими, следовательно, к системе уравнений, которая имеет заполненную, а не ленточную матрицу коэффициентов. В методе конечных элементов перемещения задаются поэлементно. Каждый узловой параметр связан только с примыкающими к этому узлу элементами, и в результате получается малозаполненная, обычно ленточная ма- трица коэффициентов.

Применения обычного метода Ритца ограничиваются относительно простыми геометрическими формами области, тогда как в методе конечных элементов простую форму должны иметь только элементы.

Еще одно различие состоит в том, что в методе конечных элементов неизвестными обычно являются узловые перемещения. Это допускает простую физическую интерпретацию. Своей популярностью метод конечных элементов в значительной степени, несомненно, обязан именно этому факту.

2.5. Критерии сходимости

Действительный минимум энергии никогда не может быть достигнут ни при каком числе разбиений, так как задание функций формы ограничивает число степеней свободы системы.

Чтобы гарантировать сходимость процесса к точному решению, необходимо удовлетворить некоторым простым требованиям. Например, очевидно, что функция перемещений должна как можно точнее описывать истинные перемещения. Нельзя выбирать функции, которые допускают деформацию элемента при перемещении его только как жесткого тела. Таким образом, первый критерий, которому должна удовлетворять функция перемещений, формулируется следующим образом:

Критерий 1. Функция перемещений должна быть выбрана таким образом, чтобы не возникала деформация элемента при узловых перемещениях, вызванных его смещением как. жесткого тела.

Это очевидное условие может быть легко нарушено при использовании некоторых типов функций. Поэтому при выборе функций перемещений следует соблюдать осторожность.

Второй критерий основывается на аналогичных требованиях. Ясно, что при уменьшении размеров элементов деформация в них будет стремиться к постоянной. Если в теле возникает однородная деформация, то желательно, чтобы она была такой и при достаточно больших размерах элементов. Можно подобрать функции, которые удовлетворяют первому критерию, но дают переменные по элементу деформации при узловых перемещениях, соответствующих условию постоянной деформации. Такие функции в общем случае не дадут хорошей сходимости и не смогут даже в пределе описать истинное распределение напряжений. Итак, второй критерий может быть сформулирован следующим образом:

Критерий 2. Функция перемещений должна быть такой, чтобы в случае, когда узловые перемещения соответствуют условию постоянной деформации, это состояние действительно реа-лизовывалось в элементе (здесь опять подразумевается обобщенная деформация).

Следует отметить, что критерий 2 согласуется с требованием критерия 1, так как перемещение элемента как жесткого тела есть частный случай постоянной (нулевой) деформации. Этот критерий впервые был предложен Базелем и др. [10] в 1965 г.

Наконец, как уже было упомянуто в разд. 2.3, неявно подразумевается, что границы раздела между элементами не дают никакого вклада в виртуальную работу. Как следствие появляется необходимость ввести следующий критерий:

Критерий 3. Функции перемещений должны быть выбраны так, чтобы деформации на границах между элементами были конечными (даже если они там не определены).

Этот критерий означает непрерывность перемещений на границе Между элементами. В случае когда деформации определяются через первые производные, как в приведенной здесь

в качестве примера плоской задаче, непрерывными должны быть только перемещения. Если же, однако, деформации определяются вторыми производными, как в задачах о пластинах и оболочках, то должны быть непрерывными также и первые производные от перемещений [2].

Последний критерий математически означает требование полноты функций , с которым читатель может более глубоко познакомиться, например, по работам [И-15]. Эвристическое доказательство условий сходимости, данное здесь, вполне достаточно для практических целей, за исключением самых необычных случаев.

2.6. Функции перемещений с разрывами между элементами

В некоторых случаях возникают существенные трудности при выборе функций перемещений элемента, которые были бы непрерывными по всей его границе со смежными элементами.

Как уже указывалось, разрывность перемещений приведет к бесконечным деформациям на границах между элементами. Этот факт не учитывался ранее, поскольку предполагалось, что вклад в энергию вносят только сами элементы.

Однако если в пределе при уменьшении размеров элементов непрерывность восстанавливается, то мы все же придем к правильному результату. Это условие практически выполняется, если:

а) условие постоянной деформации автоматически гарантирует непрерывность перемещений;

б) выполняется критерий предыдущего раздела о постоянной деформации.

В некоторых задачах, рассмотренных в этой книге, с успехом будут использоваться разрывные функции перемещений такого типа. Однако при этом нельзя уже оценить значения функционала энергии.

2.7. Предельное значение энергии деформации при использовании метода перемещений

Хотя приближенное решение, полученное методом перемещений, всегда дает завышенное значение полной потенциальной энергии X (абсолютный минимум которой соответствует точному решению), знания этого иногда бывает недостаточно для практики. В некоторых случаях, однако, можно получить более удобную оценку.

Рассмотрим, в частности, задачу, в которой отсутствуют начальные деформации или начальные напряжения. В соответ-

ствии с принципом сохранения энергии энергия деформации должна быть равна работе внешних сил, равномерно возрастающих от нуля [16]. Эта работа равна -/г^, где И7 -потенциальная энергия нагрузок. Таким образом,

или

u+jw=o

(2,32) (2.33)

на истинном или приближенном поле перемещений.

Следовательно, в данном случае приближенное решение всегда занижает значение U и полученное перемещение часто рассматривается как нижняя граница решения.

В случае когда задана только внешняя сосредоточенная нагрузка R, можно сделать вывод, что величина смещения при действии этой нагрузки будет занижена (так как U = ~

= 42Rd). При сложном нагружении эта оценка не всегда применима, поскольку для величин, представляющих практический интерес, т. е. смещений и напряжений, не удается установить определенных пределов.

Важно помнить, что оценка энергии деформации справедлива только при условии отсутствия начальных напряжений или деформаций.

Выражение для U в этом случае может быть получено из соотношения (2.31) в виде

а с помощью формулы (2.2) оно преобразуется в

и = {{бу[\[ВГ ID]lB]dv]{6} = I{6}[К] {6}.

где квадратная матрица [/(] -ранее рассматривавшаяся матрица жесткости.

Приведенное выражение для энергии всегда положительно, что следует из физического смысла этой величины. Поэтому матрица [К\, вводимая при применении метода конечных элементов, является не только симметричной, но и положительно определенной (т. е. квадратичная форма, связанная с этой матрицей, всегда больше нуля или равна нулю).

Это свойство особенно важно при использовании численных методов решения систем уравнений, так как при этом возможны некоторые упрощения.

2.8. Прямая минимизация

Тот фадт, что метод конечных элементов сводится к минимизации полной потенциальной энергии х. выраженной через конечное число узловых параметров, позволяет получить систему уравнений, символически записанную в виде (2.30). Это наиболее часто применяемый подход, особенно в линейных задачах. Однако для оценки нижней границы значения х могут быть использованы и другие, хорошо разработанные к настоящему времени методы исследования в области оптимизации процессов. В этой книге мы будем придерживаться первого способа минимизации, хотя можно использовать и другие методы [17, 18].

15 De Arrantes Oliveira Е. R., Theoretical Foundations uf the Finite Element Method, Int. J Sotids Struct., 4, 929-952 (1968).

16. De Veubeke B. F., Displacement and Equilibrium Models in the Finite Element Method, Ch. 9 in: Stress Analysis, Zienkiewicz O. C, Holister G. S., eds., Wiley, 1965.

!7. Fox R. L., Stanton E, L., Developments in Structural Analysis by Direct Energy Minimization, JAIAA. 6, 1036-1044 (1968); есть русский перевод: Фокс, Стэнтон, Достижения в области расчетов на прочность прямыми методами минимизации энергии. Ракетная техника и космонавтика, 6, № 6. стр. 55-63 (1968).

18. Bogner F. К., Malleft R. Н., Minich М. D., Schrait L. А., Development and Evaluation of Energy Search Methods in Non-Linear Structural Analysis. Proc. Conf. Matrix Methods in Struct Mech Air Force Inst. Techn., Wright Patterson A. F. Base, Ohio, 1965.

ЛИТЕРАТУРА

1. Clough R. W., The Finite Element in Plane Stress Analysis, Proc. 2nd A. S.

C. E. Conf. on Electronic Computation, Pittsburgh Pa., Sept. 1960.

2. Clough R. W., The Finite Element Method in Structural Alechanics, Ch. 7 in: Stress Analysis, Zienkievicz 0. C, Holister G. S., eds., Wiley, 1965.

3. Szmelter j., The Energy Method of Networks of Arbitrary Shape in Problems of the Theory of Elasticity, Proc. lUTAM, Symposium on Non-Homogeneity in Elasticity and Plasticity, Olszak W., ed., Pergamon Press, 1959.

4. Courant R., Variational Methods for the Solution of Problems of Equilibrium and Vibration, Bull. Am. Math. Soc, 49, 1-23 (1943).

5. Prager W., Synge j. L., Approximation in Elasticity Based on the Concept of Function Space, Quart. Appl. Math., 5, 241-269 (1947).

6. Timoshenko S., Goodier J. N., Theory of Elasticity, 2nd ed., McGrav-Hill, 1951.

7. Washizu K., Variational Methods in Elasticity and Plasticity, Pergamon Press, 1968.

8. Strutt J. W. (Lord Rayleigh), On the Theory of Resonance, Trans. Roy. Soc. (London), Aiei, 77-118 (1870).

9. RItz W., Ober eine Methode zur Losung gewissen Variations - Probleme der mathematischen Physik, /. Reine und Angew. Math., 135, 1-61 (1909).

10. Bazeley G. P., Cheung Y .K., irons B. M., Zienkiewicz 0. C., Triangular Elements in Bending - Conforming and Non-Conforming Solutions, Proc. Conf. Matrix Methods in Struct. Mech., Air Force Inst. Techn., Wright Patterson A. F. Base Ohio, 1965.

11. Михлин С. Г., Проблема минимума квадратного функционала, ГИТТЛ, М.-Л., 1952.

12. Johnson W. Al., McLay R. W., Convergence of the Finite Element Method in the Theory of Elasticity, /. Appl. Mech. Trans. Am. Soc. Mech. Eng., 274- 278 (1968); есть русский перевод: Джонсои, Маклей, Сходимость метода конечных элементов в теории упругости, Труды Американского общества инженеров-механиков. Прикладная механика, 35, сер. Е, К 2, стр. 68-72 (1968).

13. Key S. W., А Convergence Investigation of the Direct Stiffness Method, Ph.

D. Thesis, Univ. of Washington, 1966.

14. Pian T. H. H., Tong P., The Convergence of Finite Element Method in Solving Linear Elastic Problems, Int. J. Solids Struct., 3, 865-880 (1967).

3.1. Вариационные задачи

К решению встречающихся в технике задач прикладной механики существуют два подхода [1]. При одном из них используются дифференциальные уравнения, описывающие поведение некоторой произвольной бесконечно малой области. Другой подход состоит в том, что постулируется вариационный экстремальный принцип, справедливый для всей области. При этом решение минимизирует некоторую величину х> которая определяется как некоторый интеграл от неизвестных величин по всей области. Интегральную величину х, представляющую собой функцию от неизвестных функций, называют функционалом.

С математической точки зрения оба эти подхода эквивалентны, и решение, полученное при одном подходе, является решением при другом подходе. Каждый из этих подходов может быть принят в качестве основного, хотя чаще используется первый. От одного подхода можно перейти к другому с помощью математических преобразований, что является предметом многочисленАых книг по вариационным методам [2-4].

Различие между этими подходами состоит в способах получения приближенного решения. Конечно-разностные [5, 6] методы аппроксимируют дифференциальные уравнения разностными; метод Ритпа и его вариант -метод конечных элементов-связаны с приближенной минимизацией функционала.

В предыдущей главе было показано, что задача определения поля перемещений в конструкции сводится к задаче минимизации полной потенциальной энергии, определенной в виде функционала От перемещений. Была установлена эквивалентность метода конечных элементов методу приближенной минимизации функционала энергии по узловым перемещениям. В настоящем разделе этот вопрос будет рассмотрен в общем виде.

Пусть физическая (или чисто математическая) постановка задачи требует минимизации функционала % в некоторой области. Величина х определяется в виде интеграла по области V и части границы 5, на которой неизвестны функция Щ или ее производные, т. е. она имеет вид

> = SKW. -fei}. - )dV + \g{{<i>), -Ш, ...)dS. (3.1)

Пусть рассматриваемая область разделена на более мелкие части, подобласти, которые будем далее называть элементами, и пусть функции, которые мы хотим определить, для каждого элемента записываются в виде

[<1>}=т{Фу. (3.2)

Здесь (Ф) может содержать узловые значения функции, соответствующие такому элементу, или некоторые характеризующие его параметры. Неизвестная функция взята в фигурные скобки, чтобы показать, что она может быть вектором, как в примере гл. 2, а [iV]-матрица, определяющая зависимость функции формы от координат.

Для минимизации функционала х всем параметрам {Ф) полной области следует записать систему уравнений

дг д{Ф) -

<ЭФ,

= 0.

(3.3)

Если справедливо утверждение, что функционал равен сумме вкладов отдельных элементов, т. е. что

Х=Ех, (3.4),

то символическое уравнение принимает вид

ix V = 0 (3.5)

где суммирование производится по всем элементам. Таким образом, получено правило составления системы уравнений, минимизирующих функпионал, для всего ансамбля.

В частном случае, когда х является квадратичным функционалом от {ф} и ее производных, производную для элемента е можно записать в виде

= [fe]4©r + {fr, (3.6)

где [kY и {f} - постоянные матрицы. Теперь систему уравнений (3.3), минимизирующую функционал, можно записать следующим образом;

= [С]{Ф} + {Р} = 0, (3.7)

ОБОБЩЕНИЕ ПОНЯТИЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ

Суммирование производитси по всем элементам, как и в задачах строительной механики и расчета сетей, рассмотренных в гл. 1 и 2.

3.2. Критерии сходимости

Для того чтобы уменьшение размеров элементов приводило к сходимости, функции, входящие в выражение (3.1), должны удовлетворять определенным требованиям полноты.

Во-первых, при уменьшении размеров элемента функции / и g в интеграле (3.1) должны оставаться однозначными и хорошо отражать физическую сущность задачи. Таким образом, необходимо удовлетворить следующему критерию;

Критерий L Функции формы элемента [N] должны быть таковы, чтобы при соответствующем выборе {Ф} и стремлении размеров элемента к нулю можно было получить любые постоянные значения {ф] или ее производных, входящих в функционал Х-

Во-вторых, должно оставаться справедливым суммирование (3.4) и, если не добавлены поверхностные интегралы по границе между элементами [7], мы должны быть уверены, что величины, подобные fug, остаются на них ограниченными. Это возможно, если производные наивысшего порядка от <j>, входящие в выражения для функций ! w g, конечны. Таким образом, можно сформулировать второй критерий.

Критерий 2. Функции формы элемента [N] должны быть выбраны так, чтобы {ф] и ее производные, на порядок более низкие, чем производные, входящие в выражения для fag, были непрерывны на границе между элементами.

Этот критерий несложно объяснить, если представить себе что элементы разделяются между собой очень тонким слое.ч, который должен быть учтен в определяющих величину х интегралах и в котором происходит плавный переход между значениями неизвестных функций в смежных элементах. Если в пределе при стремлении толщины этого переходного слоя к нулю его вклад в х исчезает, то равенство (3.4) справедливо.

На фиг. 3.1 показана такая воображаемая переходная зона между двумя элементами. Представим себе, что скалярная функция ф определена так, что на границе раздела между элементами ее значения, полученные для каждого из элементов, равны. На фиг. 3.1, а приведен график функции, угол наклона которой принимает в переходной зоне конечное значение, хотя и претерпевает разрыв (фиг. 3.1,6). Вторая производная в этой Зоне имеет очень большое значение (фиг. 3.1, в) и стремится к бесконечности при уменьшении ширины зоны.

Следовательно, если в выражение для х входит только первая производная, то, для того чтобы гарантировать отсутствие вклада в х от переходной зоны, достаточно обеспечить непрерывность только функции ф. Однако если в функционал входит вторая производная, то справедливость равенства (3.4) не может быть гарантирована, поскольку (из-за умножения бесконечной величины на нулевую площадь) величина вклада в энергию этой зоны становится неопределенной.

	н--
	ч

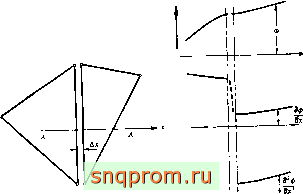
у

Стремится к-оа

Фиг 3 1 Межэлементная зона, в которой вторая производная непрерывной фукции Ф при Дх--0 становится неограниченной.

Эти два критерия являются обобщением более частных критериев разд. 2.5.

Здесь под сходимостью мы понимаем следующее; при бесконечном уменьшении размеров элементов ошибки в определении величины X стремятся к нулю. Это иногда позволяет сказать, что решение, полученное при одном разбиении, заведомо лучше решения, полученного при другом. Очевидно, что в смысле определения величины х [формула (3.2)] это утверждение справедливо, если функция формы первого типа разбиения включает все функции формы второго типа разбиения. Именно такой случай возникает, когда новое разбиение получается последующим делением более крупных элементов. Сходимость по 1 при этом будет монотонной. Это обстоятельство впервые было установлено Мелошем в 1963 г. [8].

3.3. Переменные, не связанные с узлами

Важно напомнить читателю, что при определении функции формы [равенство (3.2)] указывалось, что {Ф} содержит либо узловые значения неизвестных функций, либо некоторые параметры, характеризующие этот элемент.

Для обеспечения непрерывности функции между элементами в соответствии с требованием критерия 2 (разд. 3.2) и описания физической сущности задачи обычно рассматриваются значения величин в узловых точках. Однако всегда можно ввести дополнительные функции, принимающие нулевые значения на границах элемента и не вызывающие нарущения непрерывности, и умножить их на некоторые параметры, по которым будет минимизироваться функционал. Введение таких переменных, не связанных с узлами, может увеличить точность и иногда оказывается полезным [9].

Поскольку в общем случае эти параметры связаны только с одним элементом, минимизация по ним может быть выполнена перед составлением ансамб.1я, а сами параметры исключаются из матриц элемента.

Частным случаем неузловой переменной является хорошо известный множитель Лагранжа [3].

Он вводится в том случае, когда на функцию ф наложено дополнительное условие, не вытекающее ни из краевых условий, ни из ограничений на функции формы. Пусть дополнительное условие имеет вид

G(W) = 0. (3.10)

В эт0.м случае для решения задачи требуется минимизировать) величину

Х' = Х+Я0, (3.11)

где А, -типичный дополнительный параметр. Если наложено несколько таких условий, то минимизируется величина

(3.12)

Теперь дополнительными параметрами задачи являются величины которые опять можно связать с элементами или границами между элементами. Примеры использования таких множителей Лагранжа будут приведены ниже.

) С Доказательством этого положения можно ознакомиться в книгах по вариационному исчислению. Очевидно, что д-/дХ = О, и, следовательно, ограничение является условием минимизации. В точке экстремума х* = X. так как G == О (физический смысл X становится ясным из соотношения \=di/dG).

Интересно рассмотреть случай, когда функциоиал (3.1) представляет собой квадратичную форму и для ряда линейных ограничений на функцию Ф используются множители Лагранжа.

В общем случае можно выразить х через величины узловых параметров в виде

х={ФГ[] {Ф} + {/}ЧФ},

(3.13)

где [К] - симметричная матрица.

Вместо (3.10) линейные ограничения можно записать в матричной форме:

[О]{Ф}=0, (3.14)

где [G] -постоянная матрица. Записывая множители Лагранжа в виде вектора {%] размерности, равной числу столбцов матрицы [G] (т. е. числу ограничений), имеем

X = Y {Ф} [К] {Ф} + {FY {Ф} + ([G] {Ф}) {>.}. (3.15)

Составляя систему уравнений, аналогичную (3.6), но уже для двух множеств неизвестных, получаем

тщ \[к\ [GY(Щ^ . rwi

L[G] О JlU} ,

О

= 0. (3.16)

Здесь нужно Отметить два обстоятельства. Во-первых, система уравнений остается симметричной - факт, облегчающий применение обычных методов решения систем линейных алгебраических уравнений (гл. 20).- Во-вторых, на диагонали матрицы появляются нули, что иногда затрудняет получение решения.

В настоящей книге множители Лагранжа используются редко, исключение составляют случаи, когда приходится вводить некоторые ограничения. Типичным при.мером этого может служить ситуация, когда прн при.менении метода конечных элементов нарушаются условия непрерывности. В результате введения дополнительных условий в виде ограничений на параметры получается корректное решение. Однако в связи с тем, что такие ограничения приводят к увеличению общего числа неизвестных, появляются дополнительные трудности.

3.4. Другие подходы к методу конечных элементов

Несмотря на то что приближенная минимизация функционала-самый распространенный способ подхода к методу конечных элементов, это никоим образом не означает, что такой

1 [ 2 ] 3 4 5 ... 27