Главная страница сайта  Российские промышленные издания (узловые агрегаты) 

1 ... 15 16 17 [ 18 ] 19 20 21 ... 27

Плоское напряженное состояние и плоская деформация.

При использовании треугольных элементов, описанных в гл. 4, матрица [Л'] определяется выражением

где

[Щ = [Ш' IN Ш'п],

1 О' О 1.

-2Д--

н т. д.,

где Д-площадь треугольника, Nl задаются соотношением (4.8).

Если толщина элемента t предполагается постоянной в пределах элемента, то из уравнения (16.15) для матрицы масс имеем

или

lmY==pt\\lNr[N]dxdy [mrA = pt[I]\NrN,dxdy.

С помощью соотношения (4.8) можно показать, что

при гфз,

\\mNsdxdy

Таким образом, при получаем матрицу масс

12 I

-ц-Д при r - s. ptA = W

(16.16) (16.17)

(16.18)

i о

I Mi 0 41° i I

I 14 14 41 4l 4

4 14 14

0 i ijo i

(16.19)

Если бы масса элемента была равномерно- распределена по трем его узлам, то матрица масс имела бы вид

[тГ =

1 О О 1

0 0 0 0 0 0 0 0

о о I 1 о I о о

о о J о 1 I о о

о о [ о о М о

о о i о о i о 1

(16.20)

Очевидно, что эти результаты значительно отличаются друг от друга.

Изгиб пластины. Колебания пластин представляют собой весьма важную инженерную проблему. Такие важные явления, как колебания мостового настила, колебания лопаток турбин и др., приводят к задачам, трудно поддающимся аналитическому решению.

Важность использования согласованной матрицы масс вместо матрицы сосредоточенных масс подчеркивается в нескольких работах [15-19].

Если рассматривается, например, прямоугольный плоский элемент из разд. 10.4, то функции перемещений определяются соотношением (10.16)

(16.21)

в соответствии с обозначениями гл. 10.

Заметим, что [С] не зависит от координат, а [Р] определяется выражением

[Р] = [1, X, у, х\ ху, ж^, х^у, ху\ у^. у, xtf].

Таким образом, для плоского элемента постоянной толщины t матрица масс (16.15) принимает вид

[mY = pt ([С]-) (\ \ [PV [Р\ dx dy) [С]-. (16.22)

Как и ранее, без особых затруднений вычисляется интеграл в круглых скобках, а полная матрица масс может быть получена матричным умножением. В табл. 16.1 приводится ее явное выражение, данное Дейвом [16].

Подобные матрицы масс могут быть получены и для треугольных элементов, рассмотренных в разд. 10.6 и далее, Явные

Таблица 16.1

Матрица масс прямоугольного элемента

[М]=к

				= т [м] [L]
- 3454
-461
-461
1226	-274		3454
	-60.
				63 80
1226	-199			116 116 3454
-199	40 -42		- 116	-30 -28 -461
-274			- 116	28 30 461
	-116		1226	199 274 1226	-274	-199	3454
:б				40 42 274
-116			-274	-42 -60 -19Э			-461

-63 80

Здесь L,определяется по табл. 10.1 и А.= р/а6/6300.

Выражения для этих матриц здесь не приводятся; выполнение алгебраических преобразований предоставляются читателю).

При использовании таких элементов рекомендуются методы численного интегрирования.

Оболочки. Если определены матрицы масс для плоских и изгибных движений некоторого элемента, то может быть найдена матрица масс, отнесенная к общей координатной системе. Правила преобразований в этом случае, очевидно, точно такие же, как для сил. Основные этапы получения матрицы масс для каждого элемента в общих координатах и составление матрицы масс для-ансамбля аналогичны подобным операциям для матриц жесткости (см. гл. 11). Поэтому в принципе решение задач о колебаниях оболочек не представляет особых трудностей.

Матрицы демпфирования и другие. Приведенные выше примеры, возможно, помогли читателю закрепить некоторые общие идеи. Он легко заметит, что матрицы демпфирования, заданные уравнением (16.14), имеют точно такую же структуру, что и матрицы масс. Различные матрицы, введенные в подразд. 16.2.1 и определяемые равенствами (16.7) и (16.8), также имеют аналогичную форму. Таким образом, после незначительного видоизменения ко всем этим задачам в равной мере применимы результаты, относящиеся к. плоскому треугольному элементу, и отпадает необходимость в повторном вычислении.

16.3. Связанные задачи

Для задач обоих типов, рассмотренных в преДыДуЩем раз' деле, получены матричные дифференциальные уравнения одина- - f

) Интегралы в явном виде приведены в работе [20].

ковой формы [формулы (16.6) и (16.13)]. Аналогично могут быть получены уравнения для более сложных задач. Иногда в задачах связанного типа появляются две самостоятельные системы уравнений. Мы обсудим два таких примера, представляющих значи^ тельный практический интерес.

16.3.1. Связанное движение упругой конструкции в жидкой среде [21, 22]

Дифференциальное уравнение, описывающее распределение давления р при малых колебаниях сжимаемой жидкости, имеет вид

где с-скорость звука, а демпфирующие члены (вязкости) опущены.

На границе задается или р или величина

др дп

-p(t/ ),

(16.24)

если граница непроницаема и движется. Здесь Un есть нормальная составляющая перемещения. После разбиения жидкой об ласти на конечные элементы получается уравнение, аналогичное уравнению (16.6):

W]{p} + [G]{p) + {P}fO, (16.25)

Б котором матрицы [Я] и [G] находятся обычным способом. Матрица {FI не содержит вкладов интегрирования по объему, а обусловлена поверхностными интегралами, соответствующими описанным выше движениям [см. уравнение (15.27)]).

Движение границы (поверхности раздела) обусловлено перемещением конструкции. Если дискретизируется сама конструкция, то можно записать

U. lN]{b}, (16.26)

где [Щ определяется соответствующими функциями формы, а {6} является вектором узловых перемещений. Согласно формуле (15.13), имеем

(16.27)

{/}f = [S]{6}

1) В более общем случае в уравнение (16.25) Может входить член, содержащий первую производную от р по времени. Например, если в уравнение движения жидкости входят члены, обуслов.тенные вязким трением, или граница не отражает падающие волны давления. Такая граница имеет важное значение, если область жидкости бесконечна, а прн расчете ее нужно ограничить [22].

где

[S]=5[iVfp[yV] dS.

(16.28)

Здесь [Л^ - функции формы, определяющие распределение давления, а S - поверхность раздела жидкости и конструкции (фиг. 16.1).

После дискретизации задачи строительной механики имеем

[К\ {6} + [С] {6} -f [М\ Щ + [¥}, + [R} = О, (16.29)

где содержатся обычные члены уравнения (16.13), но воздействия разделены на заданные внещние силы [R} и силы {f)s, обусловленные, давлением жидкости на поверхности раздела. На основании принципа виртуальных работ можно найти, что силы {f}s должны быт* заданы в виде

Жидкоспн, J

(16.30)

Фиг. 16.1. Поверхность раздела твердого тела и жидкости.

так как

- Р=т{р\.

Объединяя уравнения (16.25), (16.27), (16.29) и (16.30), окончательно получаем связанную систему матричных дифференциальных уравнений

т {р} + \G\ {Р) + [S] - J {6}=о.

т щ + [С] {6} -f т ж + 7 + =°

(16.31)

Которая описывает эту задачу.

Некоторые аспекты этой задачи обсуждаются в работах [21] и [22]. В частном случае для несжимаемой жидкости (с= оо) второй член первого уравнения становится равным нулю и это уравнение может быть решено непосредственно, что дает

\u\-\s\

(16.32).

Подставив это выражение во второе уравнение, получим обычное динамическое уравнение, в котором к матрице масс

добавлена матрица присоединенных масс -hsfm- [S].

(16.33)

Такая матрица присоединенных масс, впервые предложенная Зенкевичем с сотр. [4, 15], была введена в разд. 15.5. Сравнительно недавно подобная методик.а была использована прн определении собственных частот арочных плотин [23].

16.3 2 Упругое поведение пористого насыщенного материала [24]

Эта задача встречается в механике грунтов и во многих геотехнических проблемах.

В пористой упругой среде давление жидкости в порах вызывает объемные силы, определяемые матрицей

y\- . (16.34)

Они уже рассматривались в гл. 4. Подробнее эти вопросы изложены в работе [25].

Если упругая конструкция дискретизнруется конечными э.те-ментами, то объемные силы вызовут узловые силы

/ (д1дх-\ \

\[МГ1д1ду\[Щ dV

{р}=1Ц{р}, (16.35)

где [Л?] -функции формы, определяющие перемещения упругого тела, а [Л^] - функции формы, характеризующие распределение давления ).

В результате для упругой среды мы имеем обычное уравнение дискретизированной задачи

[K]{6} + [L]{p) + {R} = 0, (16.36)

где [/С] -матрица жесткости, а {R} включает все заданные силы, кроме сил, обусловленных давлением в порах.

Переходя к рассмотрению жидкости, содержащейся в порах, следует записать соответствующее дифференциальное уравнение неразрывности. Оно уже встречалось в гл. 15 как типичное уравнение (15.1), но kx, ky, кг являются теперь коэффициентами про-

) Для простоты интегралы записываются по всей области, как гл. 1

ницаемости и Q представляет собой скорость, с которой происходит наполнение жидкости в единице объема. Для матрицы третьего порядка, связанной с компонентами перемещений, имеем

-Ш++)-Ц^1М тт. (16.37)

I д/дг)

Из уравнения (15.1) с учетом (16.37) получаем

[W]{p}-f [S]-{6}=0, (16.38)

и так как сила Q определяется уравнением (15.13), то /. Г д/дх ) \

[NVQdV \[NVid/dy

К д/dz )

[N] dV

(16.39)

Уравнения (16.36) и (16.38) образуют связанную систему совместных матричных дифференциальных уравнений. Эти уравнения аналогичны системе (16.31), полученной для связанного динамического взаимодействия жидкости и конструкции. Если пренебречь сжимаемостью жидкости, то эти системы будут иметь одинаковую форму.

. Следует заметить, что из формул (16.35) и (16.39) формально следует, что

IS] = [LV. (16.40)

Использовав несколько иной подход, Санду и Уилсон [24] впервые днскретизировали эту задачу с помощью конечных элементов. Физические аспекты этой задачи обсуждаются в работах [26, 27].

Обычное уравнение консолидации, которое имеет форму (16.1) (без вторых производных по времени), является частным случаем более общей формулировки.

Выше предполагалось, что жидкость несжимаема. Если же в задаче учитывается и сжимаемость жидкости, то в уравнении (16.38) появляется дополнительный член вида

(16.41)

Такое обобщение позволяет рассмотреть нестационарные задачи частично насыщенных грунтов.

16.4. Другой способ учета времеииого эффекта

В предыдущем разделе различные задачи были сведены к матричным дифференциальным уравнениям относительно времени. Это осуществляется достаточно просто и не требует новых принципов. Однако возможны и другие подходы.

Во-первых, к дифференциальным уравнениям, описывающим задачу, может быть непосредственно применена процедура Галеркина (или другой весовой метод минимизации невязки), обсуждавшаяся в разд. 3.4. При описании неизвестной величины функциями формы, зависящими не только от пространственных координат, но и от времени, т. е.

ф=1М{х,у,г,1)]{Ф},

дискретизация задачи может быть произведена пространственными и временными конечными элементами [6, 28]. При этом задача становится четырехмерной, но в принципе численное решение может быть получено обычным методом после непосредственной дискретизации на произвольном интервале времени U<t< к.

Во втором подходе применяется вариационный принцип по пространственным переменным и времени. Вариационные методы, использующие свертку интегралов, описаны Гэртином [29] и успешно применены в работах [5, 24]. На основе этих методов могут быть также построены пространственные и временные конечные элементы.

В простых динамических задачах вариационный принцип непосредственно следует из принципа Лагранжа. Ищется стационарное значение интеграла

Х= \i-dt, (16.42)

в котором

LU+W + T, (16.43)

где V -\- - сумма энергии деформации и потенциальной энергии, которая была уже введена в гл. 2, и Г - кинетическая энергия системы. Величина L называется функцией Лагранжа [30].

Несмотря на то что такие подходы обладают достаточной общностью, они не будут подробно рассматриваться.

Упрощенный вариант процедуры Галеркина в следующем разделе будет непосредственно использован для уравнений ди-скретизированной задачи.

16.5. Рекуррентные соотношения для решения задач Коши

В матричных дифференциальных уравнениях, полученных в предыдущих разделах, значения функций и, если необходимо,

их первых производных по времени, заданные в начальный момент времени, однозначно определяют этн функции на определенном интервале времени.

Задачи такого класса, известные как начальные нлн шаговые , могут быть решены с помошью подходящих рекуррентных соотношений [1]. В некоторых простых случаях такие рекуррентные соотношения приводят к точным решениям [3]. Эти случаи не будут рассматриваться в дальнейшем.

Рекуррентное соотношение может быть установлено различными способами. Например, может быть непосредственно использована разностная схема или применен метод Галеркина для минимизации невязки в пределах каждого интервала. Дру- той метод, который применяется чаще, обладает всеми достоинствами вариационных методов, предложенных Унлсоном и др. [5. 24].

Рекуррентное соотношение может быть записано для нескольких интервалов одновременно, что требует решения большего числа совместных уравнений, но приводит к повышенной точности и устойчивости.

Здесь удобно отдельно рассмотреть матричные уравнения, содержащие лишь первые производные по времени, и уравнения, имеющие производные второго порядка по времени.

16.5.1. Задачи, описываемые дифференциальными уравнениями первого порядка по времени

Типичной для этого класса является задача, определяемая уравнением (16.6) прн [G] = 0:

[]W-f[C]-W-f {f}=0. (16.44)

Мы рассмотрим интервал О обозначая через {}о начальные значения прн t = 0.

В общем случае предположим, что в пределах этого интервала вектор {ф} интерполирован по его некоторым значениям:

{Ф)=ZNl{t) {фЬ,

(16.45)

где Ni{t)-соответствующие функции формы, непрерывные в пределах рассматриваемого интервала.

Например, если интерполяция линейная, то следует рассмотреть лишь начальное значение ф прн = О и значение при

== At {п = 1), т. е. в матричной форме

W} = [/Vo. yV,]{J°} . (16.46)

при No = iAi - t)IM, Ni=ilM. Производная по времени

L dt

Так как начальное значение {}о известно, то используется только одна весовая невязка. Интегрируя уравнение (16.44), умноженное на Ni, имеем

+ [С\

	dN,-l
L di	df

+ {f}rf; = 0; (16.48)

после подстановки (16.46) и (16.47) и последующего интегрирования получаем

[Я] (-[ {}о + т {!},)+Tt tl (- + {Ф}д +

+ Tpr\ {nidt = 0. (16.49)

Этот результат подобен тому, который был бы получен на основе обычной центральной конечной разности [1, 4, 8]. Однако вывод уравнения (16.49) является иным, и при этом возникают интересные возможности использования других интерполяционных функций.

Из уравнения (16.49) величина может быть найдена формально:

{}. = - (т W + [С]/А^) [Я] - [Сум) {ф}о +

+ -iiT[{ntdt . (16.50)

Это рекуррентное соотношение может быть использовано Для всех последукэщих интервалов времени (выбор в качестве начального значения ф величины {}о при t = О является в данном случае чисто условным).

Для другой рекуррентной схемы можно рассмотреть некоторый интервал времени, содержащий три точки (О, 2М), как

показано на фиг. 16.2. Поступая аналогично, мы вместо уравнения (16.46) получим

W = [iVo(0> N,(t), NAt)]\ \ (16.51)

с параболическими интерполяционными полиномами Лагранжа.

Продолжение этого примера приводит к двум весовым уравнениям минимизации невязки, подобным уравнению (16.48), причем {<p}i и (}2 определяются по заданным начальным значениям {}о. Эта процедура может продолжаться до бесконечности, причем с увеличением числа совместных уравнений точность решения повышается. Ясно, что более сложные временные элементы обеспечивают большую устойчивость решения и при этом могут быть использованы большие временные интервалы.

16.5.2. Задачи, описываемые дифференциальными уравнениями второго порядка по времени

Динамические задачи строительной механики и подобные задачи описываются уравнениями вида

Фнг. 16.2. Временные функции формы с разрывной первой производной.

[К] {6} + [С\{Ь) + [М] {6} -f {F) = 0.

(16.13)

Для решения этого уравнения, очевидно, необходимы два начальных условия. Обычно задаются значения {б}о и д1д1[Ь}ц в начальный момент времени, В соответствии с, вышеизложенным функции формы, описывающие изменение конструкции во времени, выбираются по значениям {6} и dldt{b} в различные моменты времени. В случае простейшей интерполяции учитываются лишь значения времени = Ои = Д^и внутри интервала используются кубические полиномы Эрмита. Таким образом, имеем

{5} = [Яоо, Яю, Яо1, Яц]

{б}о

didt {5}о

{6}, dldt {6},

(16.52)

Яоо=1-3 2-1-253,

Яо, = 3s2 - 2s3,

H =(-s + )M и s = .

Эти полиномы Эрмита аналогичны приведенным в гл. 10 и 12; их графики представлены на фиг. 16.3.

Фиг. 16.3. Временные функции формы с разрывной второй производной.

Необходимое рекуррентное соотношение можно получить, если записать весовое уравнение минимизации невязки для

{6}о

+ [М]-щг)[Нт. Я, , Яо Я„]

дШ {б} Kdldt {6},

{f}1rf = 0. (16.53)

После подстановки функций формы и интегрирования из равенства (16.53) будут получены уравнения для определения величин {S}i и dldt{b)\, выраженных через начальные значения. Окончательный вид рекуррентного соотношения:

/4,1 /4,2 .Л21 Л22.

\dldt (6}J

.В21 В22.

(16.54)

вывод этих выражений предоставляется читателю в качестве несложного упражнения.

Полученное рекуррентное соотношение не совпадает с конечно-разностным уравнением Уилсона и Клуха [31 или с его разновидностями, использованными Чэном и др. 32]. Оно было с успехом применено Фридом [28], хотя и выведено им другим способом.

Очевидно, что можно применить и более сложные конечные временные элементы с дополнительными степенями свободы.

J6.5.3. Связанные задачи

Эти задачи могут быть исследованы изложенным выше способом с использованием различных аппроксимирующих функций по времени в соответствующей форме. Подробно этот вопрос мы рассматривать не будем.

16.5.4. Некоторые примеры

Несколько простых примеров использования рекуррентных соотношений, рассмотренных в подразд. 16.5.1, взято из работы [6] для иллюстрации применения метода и подтверждения его устойчивости.

Нестационарное распределение температуры в лопасти ротора. Пример, приведенный на фиг. 16.4, иллюстрирует двумерную задачу, описываемую уравнением теплопроводности

k at

(16.55)

Граничное условие') излучения тепла на поверхности лопасти [уравнение (15.3)] записывается в виде

аг -а(г -Гд) дп k

(16.56)

) Обычно принято граничное условие (16 56) называть условием теплообмена, а условием излучения оно называется, если в правой части (16.56) вме-CJO разности температур берется разность их четвертых степеней. -/7я л. ре.

а) I = 0,5 с

Фиг. 16.4. Распределение температур в охлаждаемой лопасти ротора, имеющей

нулевую начальную температуру (М = 0,01 с). Удельная теалоемкость c = l.U кал/Т С. Плотность р=7,99 г/см Коэффициент тепло, псоводности *-0.05кал/см.с. С. Температура газа около лопасти 1145 ?С. Коэффициент теплоотдачи а на РУ *5 ДР/ ° д , - иэменяетси от 0,390 До

Номер отверстия Температура а

в отверстии, °С

1 545 0,0980

2 687 0,0871

где f температура окружающего газа, р - плотность, с - удельная теплоемкость, й - коэффициент теплопроводности и а - коэффициент теплоотдачи.

Для конечно-элементного представления лопасти были применены изопараметрические элементы третьего порядка. Распределения температур в различные моменты времени показаны пунктирными линиями.

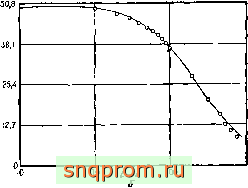
Трехмерная задача теплопроводности. Одна восьмая часть эллипсоида вращения грубо аппроксимируется тремя квадратичными изопараметрическимн элементами. На фиг. 16.5 показаны эти элементы и изменение температуры в центре эллипсоида,

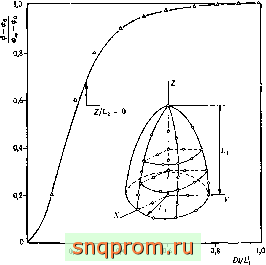
Фиг. 16.5. Изменение температуры во времени в вытянутом эллипсоиде вращения при дс = = г = о (Д/ = 0,025 с). - аналитическое решение; Д решение методом конечных злементов, 1,111=2, oLi/ft=oo.

полученное аналитически и методом конечных элементов. Наблюдается хорошее совпадение результатов.

16.6. Различные нестационарные задачи. Фильтрация со свободной поверхностью

Специальный класс нестационарных задач образуют задачи о течении грунтовых вод, в которых не учитывается сжимаемость жидкости, но происходит непрерывное изменение ее свободной поверхности. Определяющее уравнение таких задач является стационарным [уравнение (15.26)].

Свободная поверхность фильтрующейся жидкости есть поверхность нулевого давления (см. гл. 15), но она не составлена из линий тока в неустановившемся течении. Если решение задано в любой момент времени прн известном положении свобод-

ной поверхности, то может быть найдена нормальная составляющая Vn скорости фильтрации для этой свободной поверхности. Когда жидкость покидает поры, нормальная составляющая у„ скорости движения свободной поверхности может быть определена как

(16.57)

Для следующего интервала времени может быть установлено новое положение свободной поверхности и произведено повторное вычисление на основе шаговой схемы решения.

Очевидно, что сетка конечных элементов должна вьтбираться так, чтобы она соответствовала новому положению свободной поверхности на каждом шаге вычислений. Здесь особенно полезны изопараметрические криволинейные конечные элементы,

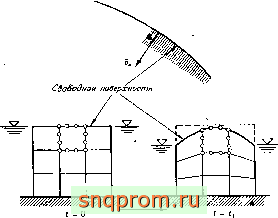
Фиг. 16.6 Фильтрационный поток прн наличии свободной поверхности. Для каждого момента времени автоматически устаиавливается сетка элементов и на.\одится скорость свободной поверхности.

30,48

а

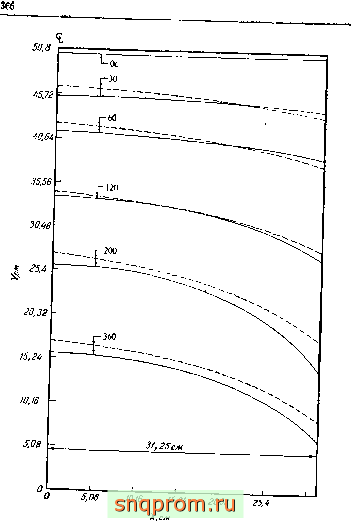
Фиг 16.7.

1000

Фиг. 16.7 (продолжение), б-изменение во времени свободной поверхности в продольной илоскоста симметрии йри быстром спуске жидкости. - аналоговое решение; о решение методом конечных элементов.

которые были использованы для решения двумерных и трехмерных задач [34, 35].

На фиг. 16,6 и 16.7 иллюстрируется применение изложенного метода к простому примеру дренажа через две симметрично выполненные траншеи и проводится сравнение с аналоговым решением этой задачи [36]. Подобное решение широко применяется на практике и позволяет получить количественные оценки в таких задачах, как быстрый спуск жидкости и т. д. Другие попытки рассмотрения нестационарной задачи этого типа перечисляются в работах [37-39].

16.7. Заключительные замечания

В настоящей главе были кратко рассмотрены некоторые типы нестационарных задач и дано изложение основных методов их решения. Подобным образом могут быть поставлены и решены многочисленные задачи, имеющие важное практическое значение.

Решения, полученные методом конечных элементов, обладают некоторыми преимуществами по сравнению с соответствующими решениями, полученными конечно-разностньши методами. Однако остаются трудности, связанные с устойчивостью таких решений, хотя неявная схема рекуррентных зависимостей, полученных в разд. 16.3, обычно является достаточно надежной.

При решении задач с помощью рекуррентного соотношения, типичная форма которого задана уравнением (16.50), появляется

необходимость вычисления матриц большого порядка на каждом шаге по времени. Если шаги по времени одинаковые и матрицы не зависят от времени, то на каждом шаге вычисления применяются одни и те же матрицы. В результате использования частичного обращения время, необходимое для вычисления на последующих шагах, может быть значительно уменьшено по сравнению с временем, затраченным на первом шаге [6].

Дальнейшую экономию времени решения можно получить, уменьшая число пространственных переменных, используя эффективный метод, подобный описанному в гл. 17 (подразд. 7.4.3), или применяя анализ Хэрти [40, 41].

К сожалению, это не относится к случаю существенно нелинейных задач, таких,-как задача о свободной поверхности (разд. 16.6) и другие задачи подобного характера. В гл. 18 будет рассмотрено несколько таких нелинейных задач. Специальная задача, относящаяся к этой группе задач, решена недавно в работе [42], где рассматривается уравнение нестационарной теплопроводности с учетом фазового превращения (затвердевания). Подробное обсуждение этой задачи и других задач подобного рода выходит за рамки этой книги.

ЛИТЕРАТУРА

1. Crandall S., Engineering Analysis, McCraw-HiU, 1956.

2. Carslow H. S., Jaeger J. C, Conduction of Heat in Solids, 2nd ed.. Clarendon Press, 1959; есть русский перевод: Карслоу Г., Егер Д., Теплопроводность твердых тел, изд-во Наука , 1964.

3. Visser W., А FiniteElement Method for the Determination of Non Stationary Temperature Distribution and Thermal Deformation, Proc. Conf. on Matrix Meth. in Struct. Mech., Air Force Inst, of Technology, Wright Patterson A. F. Base, Ohio, 1965.

4. Zienkiewicz O. C, Cheung Y. K., The Finite Element Method in Structural and Continuum Mechanics, 1st ed., McGraw-Hill, 1967.

5. Wilson E. L, Nickell R. E., Application of Finite Element Method to Heat Conduction Analysis. Nuclear Eng. and Design., 4, 1-11 (1966).

6. Zienkiewicz O. C, Parekh C. J., Transient Field Problems -Two and Three Dimensional Analysis by Isoparametric Finite Elements, Int. J. Num. Metti. in Eng.. 2, 61-71 (1970).

7. Terzhagi K.. Peck R. В., Soil Mechanics in Engineering Practice, Wiley, 1948.

8. Todd D. K., Ground Water Hydrology, Wiley, 1959.

9. Arlett P. L, Bahrani A. K., Zienkiewicz O. C, Application of Finite Elements to the Solution of Helmholzs Equation, Proc. lEE, 115, 1762-1766 (1968).

10. Taylor C, Patil B. S.. Zienkiewicz O. C, Harbour Oscillation: a Numerical Treatment for Undamped Natural Modes, Proc. Inst. Civ. Eng., 43, 141- 156 (1969).

11. Zienkiewicz 0. C, Newton R. E., Coupled Vibrations in a Structure Submerged in a Compressible Fluid, Int. Symp. on Finite Element Techniques, Stuttgart, 1969.

12 Archer J. S., Consistent Mass Matrix for Distributed Systems, Proc. Amer.

Soc. Civ. Eng., 89, ST4, 161 (1963). 13- Leckie F. A., Lindberg G. M., The Effect of Lumped Parameters on Beam

Frequencies, The Aero. Quarterly, 14, 234 (1963).

14. Zienkiewicz O. C, Cheung Y. K., The Finite Element Method for Analysis of Elastic Isotropic and Orthotropic Slabs, Proc. Inst Civ. Eng., 28, 471 (1964).

15. Zienkiewicz O. C, Irons В., Nath В., Natural Frequencies of Complex, Free or Submerged Structures by the Finite Element Method, in Symposium on Vibration in Civil Engineering, London, April 1965 (Butterworth, 1966).

16. Dawe D. J., A Finite Element Approach to Plate Vibration Problems, J. Mech. Eng. Sci., 7, 28 (1965).

17. Guyan R. J., Distributed Mass Matrix for Plate Elements in Bending, JAIAA, 3, 567 (1965): есть русский перевод: Гайан, Матрица распределенной мае сы элемента пластины при изгибе, Ракетная техника и космонавтика, 3. №. 3 (1965).

18. Bazeley G, Р., Cheung Y. К, Irons В. М Zienkiewicz О. С, Traingulai Elements in Plate Bending - Conforming and Non-Conforming Solution, Proe, Conf. on Matrix Meth. in Struct. Mech., Air Force Inst, ol Technology, Wright Patterson A. F. B se, Ohio, 1965

19. Anderson R. G., Irons B. M., Zienkiewicz O. C, Vibration and Stability of Plates Using Finite Elements, Int. J. Solids Struct., 4, 1031 - 1055, 1968.

20. Anderson R. G., The Application of the Non-Conforming Triangular Plate Bending Element to Plate Vibration Problems, M. Sc. Thesis, Univ. of Wales, Swansea, 1966.

21. Zienkiewicz O. C, Discussion of Earthquake Behaviour of Reservoir-Dam Systems* by Chopra A. K., Proc. Amer. Soc. Civ. Eng., 95, ЕМЗ 801-803 (1969).

22. Zienkiewicz O. C, Newton R. E., Coupled Vibrations of a Structure Submerged in a Compressible Fluid, Proc. Int. Svmp. on Finite Element Techniques, Stuttgart, 1969.

23. Back P. A. A., Cassell A. C, Dungar R., Severn R. Т., The Seismic Study of a Double Curvature Dam., Proc. Inst. Civ. Eng., 43, 217-248 (1969).

24. Sandhu R. S., Wilson E. L., Finite Element Analysis of Seepage in Elastic Media, Proc. Am. Soc. Civ. Eng., 95, EM3, 641-651 (1969).

25 Serafim J. L., Ch. 3 in: Rock Mechanics and Eng. Practice, Stagg K. G.. Zienkiewicz O. C, eds., Wiley, 1968.

26. Crochet J., Naghdi P. M., On Constitutive Equations for Flow of Fluid Through an Elastic Solid, Int. J. Eng. Sci., 4, 383-401 (1966).

27. Biot M A., General Theory of Three Dimensional Consolidation, /. Appl. Phys., 12, 155-164 (1941).

28. Fried I Finite Element Analysis of Time Dependent Phenomena, Int. Report. Stuttgart Univ., 1969.

29. Gurtin M., Variational Principles for Linear Elastodynamics, Arch, for Rational Mech. and Analysis, 16, 34-50 (1969).

30. Washizu K., Variational Methods in Elasticitv and Plasticity, Pergamon Press, 1968.

31. Wilson E. L., Clough R. W., Dynamic Response by Step by Step Matrix Analysis, Symp. on Use of Computers in Civil Eng., Lisbon, Oct. 1962.

32. Chan S. P., Cox H. L., Benfield W. A.. Transient Analysis of Forced Vibrations ol Complex Structural-Mechanical Systems, /. Roy. Aero. Soc, 66, 457- 460 (1962).

33. Haji-Sheikh A., Sparrow E. M., Transient Heat Conduction in a Prolate Spheroidal Solid, Trans. ASME HT. 88, 331-333 (1966); есть русский перевод- Хаджи-Шейх, Спэрроу. Нестационарная теплопроводность в удлиненном сфероидальном теле. Труды Американского общества инженеров механиков, Серия С, Теплопередача, 88, К 3, 1966,

1 ... 15 16 17 [ 18 ] 19 20 21 ... 27