Главная страница сайта
Российские промышленные издания (узловые агрегаты)
1 ...
10 11 12 [
13 ]
14 15 16 ...
27 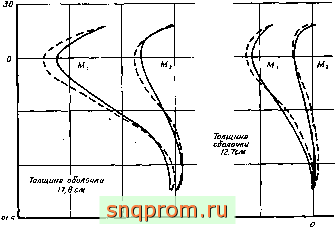
130,5
87,0
О
43,5
43,S Н-м /м в
Фиг. 11.12. Продолжение.
ся как хорошая иллюстрация достижимой точности. Результаты численного решения сравниваются с данными Албазини и Мартина [21]. На фиг. 11.10-11.12 показаны использованное разбиение и некоторые результаты. Рассматривалась несимметричная ветровая нагрузка.
Цилиндрический свод. Оболочка такого типа, часто используемая в гражданском строительстве, обычно рассчитывается методом Скордели и Ло [22]. Оболочка опирается на жесткие диафрагмы и нагружена собственным весом. На фиг. 11.13 и 11.14 сравниваютсянекоторые результаты.
Складчатая конструкция из пластин. Так как точное решение этой задачи неизвестно, сравнение проводилось с экспериментальными данными Марка и Риза [23].
Это пример задачи, для которой конечно-элементное представление физически точно. Жесткость каркаса при расчете учитывалась введением элементов балочного типа. На фиг. 11.15 и 11.16 приведены результаты решения.
Оболочка произвольной формы. На фиг. 11.17 и 11.18 представлен пример расчета оболочки довольно общей формы, опертой по центру. Чтобы показать влияние кривизны, проведено сравнение данных для тарельчатой оболочки и пластины.
1)иэ1ррэгма
R = 165
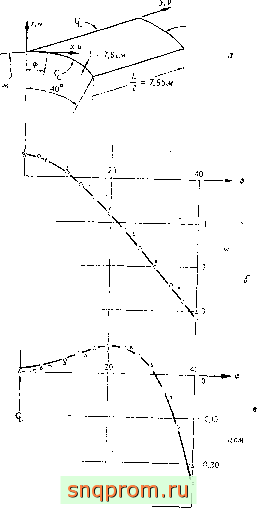
-0,45
Фиг. 11.13.
а -цилиндрический свод под действием собственного веса.
к * Яом конечных элементов и точное оешевяе №1- я =.
нне;Д сетка 8 х 12; 0 12 X 18,.
13,05
8,70
О
30 40
8,70
\1.35
о т го 30 Ф
Фиг. 11.14. Свод, изображенный на фиг. 11.13. Л, -момеит в поперечном направлении; Alj -момент в продольном навравленин в центральном сечении; Мц -крутящей момент Иа опоре.
Ре5ра жесткости ильино и 2.50/4
Жесткая диз{ррагма
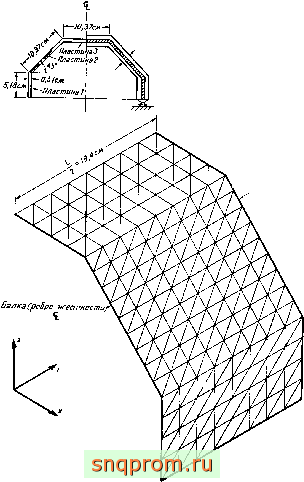
Фиг. 11.15. Складчатая конструкция из пластин [23]. Расчетная схема, нагружеиие и сетка элементов.
Я=в2,4, 10Шм v=0,43.---экспериментальные результаты;-- решение методом
конечных элементов.
Пластика | Вертикальная нагрузка, Н/м' |
| |
| 60,6 |
| 86,8 |
МааштаВ, Н О 0.-43S о,т
МзсштаВ, см 10-1 О 2JSA s.m I I 1
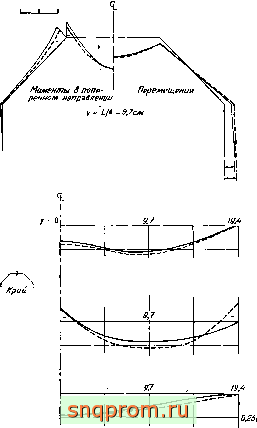
0,25cM
0,435 H I;
Фиг, 11,16. Складчатая конструкция из пластин [23]. Моменты и перемещения в центральном сечении.
а-вертикальные перемещения верхнее части; б -моменты в продольном направленна е верхнее части; в -горизонтальные перемещения края.
Радиус SS.ScM
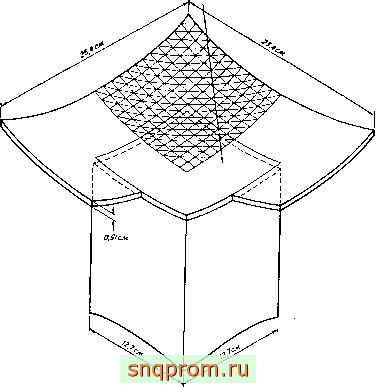
Фиг. 11.17. Квадратная тарельчатая оболочка (модель). £=6,74 . 10 Н/м , v=0,5, равномерно распределенная нагрузка 6,74 . 10 Н/м .
к
iJ S
3 5 2 S
< о
О <
s L 5
11. 7. Сходимость
Матрицы для мембранных напряжений {гл. 4) определялись в предположении непрерывности перемещений между соседними элементами. В элементах, работающих на изгиб (гл. 10), условие непрерывности также выполнялось, хотя было показано, что даже при нарущении условий непрерывности производной результаты получаются достаточно хорошими.
Функции перемещений, удовлетворяющие условиям непрерывности между элементами, лежащими в одной плоскости, в общем случае будут давать разрывные перемещения, если происходит сдвиг плоскостей элементов. Таким образом, конечно-элементная аппроксимация, использованная в настоящей главе, всегда основана на несогласованных функциях перемещений и ее сходимость можно подтвердить только экспериментально.
Если в реальной оболочке разрывов не возникает, то при уменьшении размеров элементов несогласованность становится меньше и ошибки аппроксимации реальной формы плоскими элементами и использования несогласованных функций исчезают.
Размеры разбиения, необходимого для получения приемлемой точности в. задачах теории оболочек, зависят от многих причин. Часто оказывается, что при малой толщине оболочки область действия изгибающих моментов ограничена краевой зоной, где происходит значительное изменение этих моментов. При этом мембранные силы вычисляются точно даже при очень грубом разбиении, но, чтобы уловить изменение моментов вблизи границ, требуется крайне мелкое разбиение. Однако для исследования краевого эффекта разработаны относительно простые приближенные аналитические методы, поэтому метод конечных элементов применяется главным образом для решения задач об оболочках средней толщины с различного рода неправильностями, вырезами и т. д., в которых учет изгиба так же важен, как и учет мембранных сил.
ЛИТЕРАТУРА
1. Flflgge W., Stresses in Shells, Springer-Verlag, Berlin, 1960.
2. Greene B. E., Strome D. R., Weikel R. C, Application of the Stiffness iVlet-hod to the Analysis of Shell Structures, Proc. Aviation Conf., Amer. Soc. Mech. Eng., Los Angeles, March 1961.
3. Clough R. W., Tocher J. L., Analysis of Thin Arch Dams by the Finite Element Method, in: Proc. of Symp. on Theory of Arch Dams, Southampton Univ., 1964 (Pergamon Press, 1965).
4. Argyris J. H., Matrix Displacement Analysis of Anisotropic Shells by Triangular Elements, J. Roy. Aer. Soc, 69, 801-805 (Nov. 1965).
5. Clough R. W., Johnson C. P., A Finite Element Anproximation for the Analysis of Thin Shells, J. Solids and Struct., 4, 43-60 (1968).
9 Зак, 613
6. Zienkiewicz О. С, Parekli С. J, King I. Р., Arcli Dams Analysed by a Linear Finite Element Shell Solution Program, Proc. Symp. Arch Dams., Inst. Civ. Eng., London, 1968.
7. Zienkiewicz O. C, Cheung Y. K., Finite Element Procedures in the Solution of Plate and Shell Problems, Ch.8 in: Stress Analysis, Zienkiewicz O. C, Holister G. S., eds., Wiley, 1965.
8. Zienkiewicz O. C, Cheung Y. K., Finite Element Method of Analysis for Arch Dam Shells and Comparison with Finite Difference Procedures, Proc. of Symp. on Theory of Arch Dams, Southampton Univ., 1964 (Pergamon Press, 1965).
9. Bogner F. K., Fox R. L., Schmidt L. A., A Cylindrical Shell Element, JAIAA, 5, 745-750 (1967); есть русский перевод; Богнер, Фокс, Шмнт, Расчет цилиндрической оболочки методом дискретных элементов, Ракетная техника и космонавтика, 5, № 4, стр. 170-175 (1967).
10. Contin G., Clough R. W., A Refined, Curved, Cylindrical Shell Element, AIAA Conf., Paper 68-176, N. Y., 1968.
11. Bonnes G., Dhatt G., Giroux Y. M., Robichaud L. P. A., Curved Triangular Elements for Analysis of Shells, Proc. 2nd Conf. Matrix Meth. in Struct. Mech., Air Force Inst. Techn., Wright Patterson A. F. Base, Ohio, 1968.
12. Strickland G. E., Loden W. A., A Doubly Curved Triangular Shell Element, Proc. 2nd Conf. Matrix Meth. in Struct. Mech., Air Force Inst. Techn., Wright Patterson A. F. Base, Ohio, 1968.
13. Greene B. E., Jones R. E., Strome D. R., Dynamic Analysis of Shells Using Doubly Curved Finite Elements, Proc. 2nd Conf. Matrix Meth. in Struct. Mech., Air Force Inst. Techn., Wright Patterson A. F. Base, Ohio, 1968.
14. Connor J., Brebbia C, Stiffness Matrix for Shallow Rectangular Shell Element, Proc. Am. Soc. Civ. Eng., 93, EM 43-65 (1967).
15. Carr A. J., A Refined Finite Element Analysis of Thin Shell Structures Including Dynamic Loading, SEL Rept. № 67-9, Univ. of California, Berkeley, 1967.
16. Cowper G. R., Lindberg Q. M., Olson M. D., A Shallow Shell Finite Element of Triangular Shape, /. Solids and Structs., 6, 1133-1156 (1970).
17. Utku S., Stiffness Matrices for Thin Triangular Elements of Non Zero Gaussian Curvature, JAIAA, 5, 1659-1667 (1967); есть русский перевод: Утку, Матрица жесткостей для тонких треугольных элементов ненулевой гауссовой кривизны, Ракетная техника и космонавтика, 5, № 9, стр. 150-159 (1967).
18. Ahmad S., Curved Finite Elements in the Analysis of Solid Shell and Plate Structures, Ph. D. Thesis, Univ. of Wales, Swansea, 1969.
19. Ahmad S., Irons B. M., Zienkiewicz O. C, A Simple Matrix-Vector Handling Scheme for Three Dimensional and Shell Analysis, In. J. Num. Meth. Eng., 2, 509-522 (1970).
2ft Parekh С J., Finite Element Solution System, Ph. D. Thesis, Univ. of Wales, Swansea, 1969.
21. Albasiny E. L., Martin D. W., Bending and Membrane Equilibrium in Cooling Towers, Proc. Am. Soc. Civ. Eng., 93, EM3, 1-17, (1967).
22. Scordelis A. C, Lo K. S., Computer Analysis of Cylindrical Shells, /. Am. Concr. Inst, 61 (May 1964).
23. Mark R., Riesa J. D., Photoelastic Analysis of Folded Plate Structures, Proc. Am. Soc. Civ. Eng., 93, EM4, 79-83 (1967).
12.1. Введение
Проблема расчета осесимметричных оболочек имеет большое практическое значение, поэтому в этой главе описаны специальные методы ее исследования.
Хотя для расчета таких оболочек применим и общий метод, изложенный в предыдущей главе, за счет учета осевой симметрии конструкции можно достигнуть существенных упрощений. В частности, если и оболочка и нагрузка симметричны, элемент становится одномерным. Этому простейшему типу элемента в предыдущих главах уделялось мало внимания.
Впервые к решению осесимметричных задач метод конечных элементов был применен Графтоном и Строумом [1]. В качестве элементов они рассматривали простые усеченные конусы и использовали метод перемещений. Более строгий вывод матриц жесткости проведен в работах [1-3], а предложенное Графтоном и Строумом [1] обобщение метода на случай несимметричной нагрузки подробно описано в работах [4-6].
Позднее появилось много работ, посвященных применению криволинейных элементов и улучшению с их помощью используемых аппроксимаций. Привести здесь полный список литературы практически невозможно. В работах [7-10] показываются возможности применения различных криволинейных координат, а в статьях [9, 11J обсуждается использование для повышения точности дополнительных неузловых степеней свободы.
В осесимметричных оболочках, как и в любых других, существуют и изгибные и мембранные усилия. Они однозначно определяются величинами обобщенных деформаций, под которыми в данном случае понимаются растяжения и искривления срединной поверхности; Если перемещения каждой точки срединной поверхности известны, то такие деформации и результирующие внутренних напряжений, или просто напряжения, определяются по формулам, которые можно найти в обычных курсах теории оболочек.
Например, перемещение точки срединной поверхности осе-симметричной оболочки (фиг. 12.1), находящейся под действием осесимметричной нагрузки, однозначно определяется двумя компонентами и и да по касательной и нормали к поверхности.
ОСЕСИММЕТРИЧНЫЕ ОБОЛОЧКИ
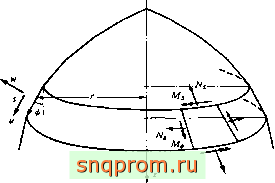
Фиг. 12.1. Осесимметричиая обо.точка, перемещения и результирующие напряжений. Оболочка представлена в виде набора конических оболочек.
При условии, что угол ф не меняется, четыре компоненты деформации определяются следующими выражения [12]:
ffi) cos 0 -)- а sin Ф
{e} =
d ds
sin Ф dw
(12.1)
r ds
Им соответствуют четыре результирующих напряжения, показанные на фнг. 12.1, которые связаны с деформациями матрицей упругости [D]:
{а} =
= [D]{e}.
(12.2)
Для изотропной оболочки матрица [D] имеет вид
(12.3)
где верхняя часть ее характеризует действие мембранных усилий, а нижняя представляет собой матрицу изгибных жесткостей, причем сдвиговые члены в обеих частях опущены.
12.2. Характеристики элемента. Осесимметричные нагрузки. Прямолинейные элементы
Пусть узловыми поверхностями оболочка разбита на ряд усеченных конусов (фиг. 12.2). Перемещения узловых точек i и
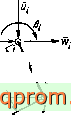
Фиг. 12.2. Элемент осесимметричной оболочки.
/ однозначно определяют деформации элемента через заданную функцию перемещений.
В каждой узловой точке задаются осевое и радиальное смещение и поворот. Поскольку оболочка работает иа изгиб, необходимы все эти три компоненты. Таким образом, перемещение точки i определяется тремя компонентами, причем первые две соответствуют глобальным координатам
(12.4)
Следовательно, элемент с двумя узлами / имеет шесть степеней свободы, которыми являются перемещения элемента
(12.5)
Перемещения внутри элемента должны единственным образом определяться перемещениями узловых точек (б} и координатой S и удовлетворять условиям непрерывности углов накло-
на н перемещении
(12.6)
Если положить, что и зависит от 5 линейно, а w является полиномом третьей степени от s, то получим щесть неизвестных постоянных, которые можно определить по узловым значениям , ш и р. В узле i
cos sin # 0 - sin cos 0 0 0 1J
Л = ШЬЛ. (12.7)
Записывая
u = a, + ajS, легко составить щесть уравнений и найти')
(12.8)
| | | | | | |
| l-3s-f2s | L (s-2s2 + s3) | | 3s2 2s3 | | |
где
(12.9)
Обозначая через матрицу размерности 2X6, можно записать
Щ о о \ц\
W=[[ivj] [Л], [jv;] [А]] {6} = \щ {5}
(12.10)
) функции, которые при этом появляются, представляют собой иолнвомн Эрмита нулевого и первого порядков (см. разд. 10.14),
Используя определение (12.1), нетрудно по (12.10) получить матрицу деформаций [В]:
где
1В,] =
{е} = [В]{бГ = [[В(][Л], [В,][Я]]{5Г,
(12.11)
| . 0 | |
- 5) sin Ф | (1 -Зз + 2з')совф | Z. (s- 2s2 + s3) cos Ф |
г | г | |
| (6-12/) | (4-6s) Z. |
| (6s - 6s2)sin0 | (-1 -f 4s- 3s2) sin Ф |
| |
lB/] =
s sin Ф
(3s - ?s) созФ r
(-6+ l?s) L
(-6s + 6s) sin 0 rL
Z.(-s-bs3)cos. r
(2 - 6s)
£
(2s - Ss ) sin Ф r
(12.12)
Теперь известны все составляющие, необходимые для составления матрицы жесткости (или матрицы нагрузки, перемещений, напряжений и начальных напряжений) по стандартным формулам гл. 2. Интегрировать надо по площади А элемента, т. е.
dA = 2лг ds = 2nrL ds,
где s изменяется от О до 1.
Следовательно, в соответствии с (2.10) имеем 1
[/е]= [ВПО] [В] 2nrL ds.
(12.13)
(12.14)
Типичная подматрица этой матрицы имеет вид
[U= txrj [BrV[D][B,]rds [I] 2п1. (12.15)
Перед интегрированием необходимо выразить радиус г через S.
Как н раньше, удобно использовать численное интегрирование. В работе Графтона и Строума [1] приведены явные выражения для матрицы жесткости, полученные на основе вычисления
лишь ОДНОГО среднего значения подынтегральной функции и при использовании матрицы [D\ ортотропного материала. Даже такая грубая аппроксимация позволяет получить очень хорошие результаты при условии, что размеры элементов малы.
Перси и др. [4] и Клейн [5] провели численное интегрирование по семи точкам и получили несколько улучшенную матрицу, хотя она и не приведена в явном виде.
Следует помнить, что если заданы действующие по окружности нагрузки или моменты, то в расчеты должно закладываться их полное окружное значение, так же как это делалось в случае осесимметричных тел, рассмотренных в гл. 5.
12.3. Примеры и точность
Для рассматриваемых здесь осесимметричных оболочек условия непрерывности выполняются. Поэтому для полигональных оболочек всегда будет наблюдаться сходимость.
Проблема аппроксимации криволинейной оболочки полигональной аналогична проблеме, рассмотренной в гл. И. Числовые расчеты подтверждают ожидаемую сходимость.
Когда нагрузка вызывает в основном мембранные напряжения, даже при достаточно мелком разбиении наблюдается некоторое расхождение в значениях изгибающих моментов. Однако с дальнейшим уменьшением размеров разбиения оно исчезает, особенно если при расчете значения моментов усредняются. Это необходимо делать для исключения влияния замены оболочки набором усеченных конусов. На фиг. 12.3 и 12.4 показано несколько типичных примеров, взятых из работы Графтоиа и Строума [1].
12.4. Криволинейные элементы и их функции формы
В гл. 8 уже рассматривались искривленные (криволинейные) Элементы, причем в выражение для деформации входили только первые производные. В данном случае это выражение содержит вторые производные [см. (12.1)], и поэтому некоторые теоремы гл. 8 здесь неприменимы.
Ранее упоминалось, что для исследования осесимметричных оболочек предложено множество криволинейных элементов [7-10]. Элемент, описанный здесь, получен Айронсом и Делпа-ком [9]; в соответствии с терминологией гл. 8 он относится к элементам субпараметрического типа.
Основой для определения криволинейного элемента служит общая касательная между смежными элементами (или заданное направление касательной). Это необходимо, чтобы избежать изломов прн описании практически гладкой оболочки.
. 7.62
Ш-1.27
0,25 0.50 0J} W0 as ISO
X, CM
и = 0,30 171 Н/м tO.OJCM
г,54см

Г-12,7см
5.0ecM\5,oelMj
Случай! Sпо0,51 см Сл11чайг OioOSc Случай 3 W по 0.13 см в
0,25 0,5 0,75 100 ЦБ 1,5 2.0 X. СМ
Число элементов
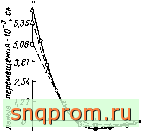
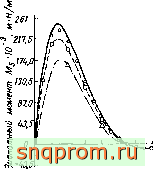
Фиг. 12.3. Расчет цилиндрической оболочки методом конечных элементов
(Графтои и Строум, JAlAA, 1963). а: -теоретическое решение; Д случай 1, ошибка определения максимального перемещения 31,7%; □ случай 2, ошибка опредеденяя максимального перемещения П,1?6: О случай 3, ошибка определения максимального перемещения 3,1 ?й.
б; -теоретическое решение; Д случай 1, ошибка определения максимального мо-
ыента 28,8? ; D случай 2. ошибка определения максимального момента \X-fi%; О случай 3, ошибка дпределеаия максимального момента 2)5?,
V = 0,33
Расположение узлов М с интервалом 0,5°
7 с интервалом 1,0 .3 с интервалом 2.0°
с интервалом
5,0В\-
. 3.S1
г, 54
| | -теоретическое решение о расчетные аначвния |
| \ Момент |
Перемещение | \ 1 >1 1 |
| Ъ 35 40 °>>->л=2:-- |
| |
осыо вращения f, spaff
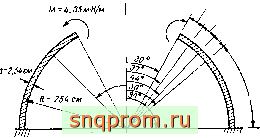
Фиг 12 4 Расчет полусферической оболочки методом конечных элементов (Графтон и Строум, JAIAA, 1963).
Сначала рассмотрим прямолинейный исходный элемент, для которого неизвестная функция ф выражается через свои узловые значения и значения углов наклона в точках 1, 2 (фнг. 12.5). Координата изменяется от -1 до -fl (как в примере гл. 8).
Используя принятые обозначения, можно записать
=E(iv{(+Ar()j=m{?r. (12.16)
Здесь Л' и N - скалярные функции формы, которые при задании в виде полинома имеют третий порядок Гкак в соотношении (12.9) для W].
Гг- г,

Фиг. 12.5. Криволинейный изопараметрнческий элемент оболочки для осесимметричных задач, а -исходный элемент; б -криволинейные координаты.
Эти функции записываются в виде
(12.17)
где о = Ы-
Их можно одновременно использовать и для описания закона изменения глобальных перемещений Д и ш') и для задания координат г и 2 оболочки (срединной поверхности).
) Отличие от предыдущего случая состоит в том, что теперь обе ком-, поненты перемещений в элементе изменяются по крайней мере по кубиче- скому закону, тогда как ранее допускался линейный закон изменения тангенциального перемещения. Однако при условии, что толщина оболочки изменяется непрерывно, эта дополнительная степень свободы не приводит к чрезмерным требованиям непрерывности.
Если толщина элемента переменная, то и ее закон изменения можно аппроксимировать этими же функциями.
Элемент такого типа будет нзопараметрическим (см. гл. 8).
Таким образом, геометрию оболочки можно характеризовать координатами
(12.18)
При заданных узловых значениях эти соотиощения устанавливают взаимно однозначное соответствие между и положением точки на поверхности криволинейного элемента (фиг. 12.5,6).
Координаты ri и г,- известны, кроме них, на концах известны только углы наклона
Значения производных, входящих в ба I вдоль касательной s. Задано только соотношение
(12.19)
12.18), зависят от масшта-
(12.20)
Производные (drldl)i или (dzidl) могут в принципе иметь произвольную величину. Здесь, однако, необходимо учитывать практические соображения, так как при некоторых значениях производных можно получить негладкую зависимость между s и При неудачном выборе кривая может быть негладкой и образовывать петлю между узлами.
Для того чтобы получить достаточно гладкие поверхности, можно положить
замечая, что длина всего интервала \ между узлами равна 2.
12.5. Выражения для деформаций и свойства криволинейных элементов
До сих пор речь шла о представлении глобальных перемещений, хотя деформации в соответствии с (12.1) определяются через производные от локальных перемещений по касательной s.
Поэтому, для того чтобы получить выражения для деформаций, требуется произвести некоторые преобразования.
Если принять, что изменение глобальных перемещений описывается функцией формы (12.16)
(12.22)
то с помощью преобразования (12.7) легко найти локальные перемещения и, W ъ виде
COS i(i sin i(i
(12.23)
где -угол между касательной к кривой и осью z (фиг. 12.5). Этот угол надо выразить через координату g. Очевидно, что
=-(*)/(f)-
(12.24)
и, следовательно, использование формул (12.18) позволит сделать это.
Посмотрим далее, можно ли наложить условия непрерывности в узлах на параметры, входящие в (12.22). Ясно, что глобальные перемещения должны быть непрерывны. Однако в предыдущих случаях требовалась непрерывность только угла поворота касательной. Здесь же требуется непрерывность производных от перемещений по s. Следовательно, величины
dw ds
в узлах смежных элементов должны иметь одинаковые значения.
Поскольку
da da I ds dw dw / ds
ds ds
dll dl ds dll dl
(12.25)
при подстановке этих новых переменных в выражения (12.22) и (12.23) не возникает никаких трудностей. В результате они прн-
1 ...
10 11 12 [
13 ]
14 15 16 ...
27

