Главная страница сайта  Российские промышленные издания (узловые агрегаты) 

1 ... 9 10 11 [ 12 ] 13 14 15 ... 27

11.1. Введение

Оболочка, по существу, представляет собой конструкцию, которая может быть получена нз тонкой пластины путем предварительного деформирования срединной плоскости в поверхность одинарной илн двойной кривизны. Хотя предположения о распределении деформаций н напряжений в поперечном направлении остаются в силе, оболочка совсем по-другому, нежели пластина, воспринимает внешние нагрузки. Результирующие напряжений на площадках, параллельных срединной поверхности оболочки, теперь имеют компоненты, нормальные к этой поверхности, и уравновешивают основную часть нагрузки. Это обстоятельство объясняет экономичность оболочек как несущих конструкций и нх популярность.

Вывод основных уравнений, описывающих поведение оболочки, связан с большими трудностями и в зависимости от введенных допущений приводит к различным формулировкам. Классическая теория оболочек подробно изложена во многих учебниках по этому предмету, например в хорошо известной книге Флюгге [1].

Применение метода конечных элементов к решению задач теории оболочек, рассматриваемое в этой главе, устраняет упомянутые выше трудности за счет введения дополнительного допущения. Оно носит скорее физический, чем математический характер. Предполагается, что поведение непрерывной криволинейной поверхности достаточно точно характеризуется поведением поверхности, составленной из малых плоских эле.ментов.

Из физических соображений следует, что с уменьшением размеров элементов решение должно сходиться и, как показывает опыт, такая сходимость действительно наблюдается. Особого внимания требует способ задания узловых нагрузок (нлн массовых сил). В приведенных примерах нагрузка и массы в узлах распределялись так, чтобы наилучшим образом воспроизвести локальные эффекты. Теперь в связи с заменой криволинейной поверхности набором пластин более правильно представлять распределенную нагрузку в виде статически эквивалентных сосредоточенных узловых сил. Это, возможно, лучше всего иллюстрируется простой задачей о круглой арке (фиг. 11.1). Круг-

лая арка под действием равномерно распределенной нагрузки гораздо лучше аппроксимируется многоугольной аркой, нагруженной статически эквивалентными сосредоточенными силами, как показано на фиг. 11.1,6, чем такой же аркой Д Действием равномерно распределенной нагрузки (фиг. 11.1, в). Это можно проверить, построив соответствующие многоугольники сил.

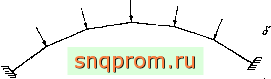
Фиг. 11.1. Представление криволинейной арки набором прямых.

Элементы оболочки находятся в общем случае под действием изгибающих и мембранных снл, действующих в плоскости. В плоских элементах эти силы вызывают независимые деформации при условии, если они малы; поэтому, чтобы составить матрицы жесткости, можно воспользоваться уже изложенным материалом.

Для представления произвольной оболочки в виде набора плоских элементов можно использовать только треугольные элементы. Несмотря на то что эта идея была предложена Грином н др. [2} еще в 1961 г., успеху мешало отсутствие хорошей матрицы жесткости для плоского треугольного элемента при изгибе [3-6]. Улучшение элементов, получаемое изложенными п гл. 10 способами, позволяет хорошо описывать поведение оболочек, разбитых на плоские элементы.

ОБОЛОЧКИ КАК СОВОКУПНОСТЬ ПЛОСКИХ ЭЛЕМЕНТОВ

Некоторые оболочки, например цилиндрические, можно представить в виде набора плоских элементов прямоугольной или четырехугольной формы. Наличие хороших матриц жесткости для этих элементов позволило получить удовлетворительные результаты, С помощью элементов именно такого типа были решены практически важные задачи проектирования арочных плотин и другие задачи для перекрытий цилиндрической формы [7-8].

Очевидно, что возможности исследования оболочечных конструкций методом конечных элементов неисчерпаемы. При наличии общей вычислительной программы проблемы, связанные с наличием отверстий, переменной толщины и анизотропными свойствами, становятся несущественными.

Особый случай представляют осесимметричные оболочки. Хотя, очевидно, их можно рассматривать с помощью метода, изложенного в настоящей главе, к ним применим и более простой подход. Ему будет посвящена гл. 12.

К решению рассматриваемых здесь задач можно подойти и по-другому, а именно используя криволинейные оболочечные элементы. При этом необходимо применять криволинейные координаты, методы введения которых описаны в гл. 8. Допущение о представлении оболочки набором плоских элементов теперь исключается за счет использования той или иной теории оболочек. Несколько вариантов применения метода перемещений описано в работах [9-18].

Одни из самых простых и эффективных способов построения криволинейных оболочечных элементов состоит в использовании теории так называемых пологих оболочек [14, 16],

Здесь W, и, V являются нормальной и тангенциальными компонентами перемещений криволинейной поверхности, и если считается, что все элементы касаются друг друга, то нет необходимости переходить от локальных к глобальным значениям.

Предполагается, что элемент является пологим относительно локальной системы координат в плоскости, проходящей через его узловые точки, а энергия деформации элемента определяется соответствующими выражениями, содержащими производные по координатам в плоскости проекции. В результате можно использовать такие же функции формы, как и для рассматриваемых в этой главе плоских элементов, причем здесь интегрирование, как и ранее, проводится в плоскости.

Пологие оболочечные элементы, в выражении для энергии Которых содержатся члены, характеризующие взаимное влияние друг на друга мембранных и изгибных деформаций, несколько более эффективны, чем плоские элементы, для которых взаимное влияние учитывается только на границе. Максимальную эффективность имеют простые элементы небольших разме-

ров, но для более сложных крупных элементов все преимущества пропадают. Очень хорошо использование пологих элементов описано в работе [16].

Однако во многих практических случаях плоские элементы дают хорошую аппроксимацию, и, кроме того, они позволяют производить простое соединение с подкрепляющими элементами и шпангоутами, что не всегда удается при использовании криволинейных элементов. В самом деле, во многих практических задачах вся конструкция или по крайней мере часть ее, по существу, составлена нз плоских Поверхностей, а такие поверхности легко аппроксимируются. По этим причинам криволинейные тонкие оболочечные элементы рассматриваться здесь не будут, а вместо этого в гл, 13 будет изложен общий подход к решению задач о толстых криволинейных оболочках (на основе трехмерного анализа, что дает возможность избежать неточностей уравнений теории оболочек),

В следующей главе, посвященной осесимметричиым оболочкам, будут применяться как плоские, так и криволинейные элементы.

11.2. Жесткость плоского элемента в локальных координатах

Рассмотрим типичный плоский элемент, находящийся одно-временио под действием мембранных и изгибающих сил (фнг. 11.2).

Остановимся сначала на действии мембранных сил (плоское напряженное состояние). Из гл. 4 известно, что деформированное состояние однозначно описывается величинами перемещений и н V каждой узловой точки (. Минимизация общей потенциальной энергии приводит к матрицам жесткости

= [k]i

(11.1)

где

Аналогично деформированное состояние, вызванное изгибом, однозначно определяется узловым смещением w в направлении оси Z и двумя углами поворота 6.. и Э . Это позволяет представить матрицы жесткости в виде

(11.2)

где

Прежде чем объединить этн матрицы, важно отметить два обстоятельства. Во-первых, перемещения, вызванные мембранными силами, не влияют на изгибные деформации н наоборот. Во-вторых, угол поворота 9z не входит в число узловых параметров, определяющих деформации. Хотя на этой стадии пово-

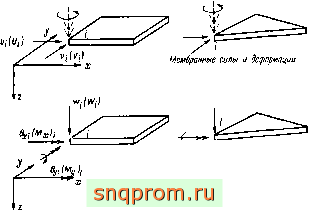
Ишбающш силы и изЫные дефориациц

Фиг. 11.2. Плоский элемент под действием мембранных и изгибающих счл.

ротом вокруг осн Z можно пренебречь по причинам, которые станут ясными позднее, уже сейчас прн составлении ансамбля элементов целесообразно учесть этот поворот и связать его с фиктивным моментом М^. Тот факт, что 9 не участвует в процессе минимизации, просто учитывается включением соответствующего количества нулей в матрицу жесткости. Записывая теперь узловые перемещения в виде

Щ

(11.3)

и соответствующие силы как

получаем

или

Ui Vi Wi Mi

(11.4)

= [fe]

(11.5)

Нетрудно видеть, что матрица жесткости состоит из следующих подматриц:

( 1-

если учесть, что

[О О OiO

о о1io

О 01 [krs] \о

О о] \о

(11.6)

(11.7)

Этн соотношения справедливы для любого многоугольного элемента, и в частности для двух важных случаев, иллюстрированных на фнг. 11.2.

11.3. Переход к глобальным координатам и составление ансамбля элементов

Полученная в предыдущем разделе матрица жесткости записана в локальной системе координат, так как компоненты изгибающих н мембранных сил выражены в локальных координатах.

Преобразование к глобальным координатам (которые будем обозначать через х, у, z в отлнчие от локальных координат х',

у', г') необходимо для составления ансамбля элементов и записи соответствующих уравнений равновесия.

Кроме того, координаты узлов удобнее задавать в глобальной системе, а затем переходить к локальным координатам, т. е. осуществлять обратное преобразование. К счастью, все преобразования достаточно просты.

На фиг. 11.3 показаны две системы координат. Узловые силы и перемещения преобразуются из глобальной в локальную си-

Фиг. 11.3. Лока.чьные и глобальные координаты.

стему координат с помощью матрицы [L]:

{6i} = [L]{6,}, {F[} = [L\{Fi},

где

[il =

к О

L0 ?.J

(11.8) (11.9)

а [%] представляет собой матрицу размерности 3X3 косинусов углов между осями этих систем, т. е.

(11.10)

		у'у	у'г

где 1х-х- косинус угла между осями и л и т. д.

Следовательно, для полной системы узловых сил элемента можно записать

{(,у = [т]{ьу, {Fr = [T\{Fy.

(11.11)

По правилам ортогональных преобразований (см. разд. 1.4) матрица жесткости элемента в глобальных координатах принимает вид

[k] = [TVlk][T]. (11.12)

В обоих последних соотношениях

L О О ...

1Т] =

О L О О О L

(11.13)

и является диагональной матрицей, составленной из нескольких матриц [L], количество которых равно числу узлов элемента.

Неслож.ю показать, что типичная подматрица жесткости записывается как

lkrs]=lLV[krs][L], (11.14)

где подматрица [krs] в локальных координатах определяется соотношением (11.6).

Определение локальных координат осуществляется аналогичным образом. Если начала локальной и глобальной систем координат совпадают, то

(11.15)

Так как при получении матрицы жесткости положение начала координат несущественно, то такого преобразования всегда достаточно для определения локальных координат в плоскости элемента (или в плоскости, параллельной ему).

После получения матриц жесткости всех элементов в общей глобальной системе координат составление ансамбля элементов и окончательное решение производятся обычным образом. В результате искомые перемещения определяются в глобальной системе координат, и для определения напряжений необходимо в каждом элементе перейти к локальным координатам. После этого можно использовать обычные матрицы мембранных и изгибающих напряжений.

П.4. Жесткость фиктивного поворота

Если все элементы, пересекающиеся в узле, компланарны, то прн использовании описанного подхода встречаются некоторые трудности, связанные с тем, что жесткость в направленнн Qzi (фиг. 11.2) равна нулю.

В такой точке последнее нз шести уравнений равновесия (со--ответствующее направлению вг) в локальных координатах обращается в равенство

0 = 0. (11.16)

Само по себе уравнение такого типа не вносит особых трудностей (хотя в вычислительной программе может привести к ошибочным результатам). Однако если направления глобальных и локальных осей координат отличаются, то после соответствующего преобразования получаются шесть на первый взгляд корректных уравнений. Эта система будет особенной, ибо она содержит равенство (11.16), умноженное на действительные числа').

Существуют две возможности обойти эту трудность:

а) составить систему уравнений для ансамбля в точке, где элементы компланарны, в локальной системе координат (и исключить уравнение 0 = 0);

б) ввести в этой точке некоторый произвольный коэффициент жесткости кёг- Это приведет в локальных координатах к замене уравнения (11.16) уравнением

кёгвг! = 0.

(11.17)

Последнее после преобразований позволяет получить хорошо обусловленную систему уравнений ), нз которой обычным способом находятся все перемещения, включая бгг- Так как бг,- не входит в уравнения равновесия и напряжения от него не зависят, величине жесткости kez можно придать произвольное значение. Результат при этом не изменится.

Оба предложенных способа связаны с определенными трудностями программирования (хотя второй несколько проще). В работе [15] приведены результаты определения реального коэффициента жесткости для дополнительных степенен свободы типа описанных поворотов.

) Читатель может вспомнить логическую ошибку в доказательстве равенства 2 = 4 и другие, основанные на умножении обеих частей равенства (11,16),

) По-вндимому, автор имеет а оиду разрешимость приведенной системы уравнений (11.5) Для хорошей обусловленности, кроме однозначной разрешимости, требуется еще малость изменения решения этой системы при малом изменении правых частей (см. С. Н. Годунов, В. С. Рябенький, Разностные схемы, изд-во Наука , гл. 2, § 4, 1973 г.).-Прим, ред.

В программе, неоднократно применявшейся автором [6], использовалась система фиктивных коэффициентов жесткости поворотов для всех элементов, как компланарных, так и некомпланарных. Для треугольных элементов оин вводились в виде такой матрицы, что равновесие в локальных координатах не нарушалось, т. е.

1 - 0,5 - 0,5 1 -0,5 L Симметрично 1 J

(11.18)

где а - некоторый коэффициент, который следует еще задать.

Из-за того что дополнительные жесткости вводятся в некомпланарных узлах, их величины влияют на результат, так что этот прием является приближенным. Однако изменение в довольно широких пределах величины коэффициента а мало сказывается на конечном результате. Например, в приведенной ниже табл. 11.1 содержатся величины перемещений арочной плотины для различных значений а, взятые из работы [2].

Таблица 11.1

Узловые коэффициенты жесткости поворота в арочной плотине 2]

а	1,00	0,50	0,10	0,03	0,00
Радиальные перемещения, мм	61,13	63,35	64,52	64,78 .	65,28

Из таблицы видно, что прн а = О перемещения близки к точным. На практике рекомендуется использовать значение а = 0,03 илн ниже.

Некоторые авторы [5] пытаются избежать этой трудности за счет уменьшения числа степеней свободы, пренебрегая одной нз них и объединяя все уравнения по нормали к оболочке. Этот метод используется в гл. 14. Однако он в свою очередь вносит новую трудность, так как если учесть действительное изменение направлений в оболочке, то не так просто задать нормаль .

11.5. Локальные направляющие косинусы

После определения матрицы направляющих косинусов [?.]для каждого элемента решение задачи не представляет никаких трудностей и производится обычным образом. Однако само

определение матрицы направляющих косинусов приводит к некоторым алгебраическим трудностям; это определение не единственно, так как направление одной нз осей, лежащей в плоскости элемента, произвольно.

Рассмотрим сначала совокупность прямоугольных элементов, для которой матрица направляющих косинусов находится особенно просто.

11.5.1. Прямоугольные элементы

Такие элементы применяются только для аппроксимации цилиндрических и коробчатых поверхностей. При этом удобно

Фиг. 11.4. Цилиндрическая оболочка как совокупность прямоугольных элементов. Локальные и глобальные координаты.

направить одну из сторон элемента и соответствующую ось локальных координат х' параллельно глобальной оси х. Для типичного элемента ijkm (фиг. 11.4) легко определить все соответствующие направляющие косинусы.

Очевидно, что для оси х' направляющие косинусы имеют вид V = 0, (11.19)

lxz=-0.

Направляющие косинусы оси у' выражаются через координаты различных узловых точек. Выражения

Хуу = + yz =

У) - Ус

-{yi-yif}

(11.10)

л/{{1Т'>? + {У,~У1Г}

представляют собой простые геометрические соотношения-, которые получаются из рассмотрения вертикальной секущей плоскости, проходящей через точки .

Рассматривая то же сечение, для оси г' получаем

Xzx = О,

{(i-if + iyi-yif] у, - У;

(11.21)

Ясно, что для сохранения правильных знаков выражений важен порядок нум(фации узловых точек.

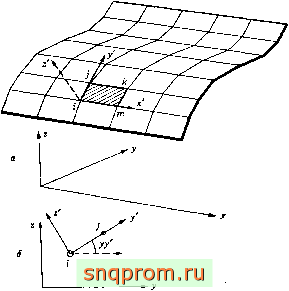
11.5.2. Произвольно ориентированные в пространстве треугольные элементы

На фиг. 11.5,0 показана произвольная оболочка, разбитая на треугольные элементы. Все элементы ориентированы по отношению к координатным плоскостям совершенно произвольно. Определить локальные оси и их направляющие косинусы в этом случае значительно сложнее, чем в предыдущем более простом примере. Проще всего эта задача решается с использованием векторной алгебры; читателям, которые успели забыть ее основы, полезно обратиться к приложению 5.

Направление одной из локальных осей произвольно, и ее выбор должен быть сделан заранее. Будем считать, что ось х' направлена вдоль стороны треугольника, как показано на фиг. 11.5,6.

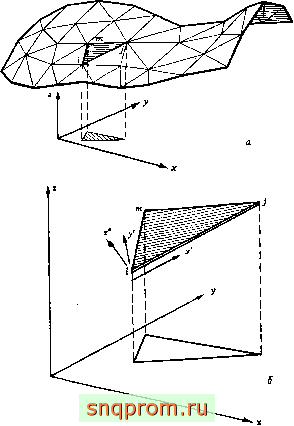
Фиг. 11,5.

а -ансамбль треугольных элементов, аппроксимирующий произвольную оболочку; б -локальные и глобальные координаты для треугольного элемента.

Эта сторона определяется вектором Vij с глобальными координатами:-

Vi, = \yi-yi\. (11.22)

Направляющие косинусы получаются делением компонент этого вектора на его длину, т. е. в виде компонент вектора единичной длины:

f.=t, = J-j/,!, (11.23)

где

Здесь для краткости положено % = Xj - xi и т. д.

Направим ось г' перпендикулярно плоскости треугольника. Это направление в соответствии со свойствами векторного произведения можно определить как векторное произведение двух сторон треугольника

yilZml - Zfiymi

(11.24)

т. е. нормальным к плоскости треугольника вектором, длина которого по определению (см. приложение) равна удвоенной площади треугольника. Таким образом,

L = /{У1,гш1-гцУт1?+ {...?+{.? = 2Д.

Направляющие косинусы оси г' получаются просто как направляющие косинусы вектора Уг \ их можно представить в виде единичного вектора

2Д

(11.25)

Наконец, направляющие косинусы оси (/ получаются как направляющие косинусы вектора, нормального одновременно к осям х' и г'. Так как векторы единичной длины в каждом из этих направлений фактически определены соотнощениями (11.23) и (11.25), имеем

> = VzX Vx =

(11.26)

без деления на длину, которая в данном случае равна единице.

Все векторные операции можно записать в виде специальной подпрограммы, автоматически осуществляющей векторное умножение, нормировку (т. е. деление на длину) и т, д. [19], но-

этому нет необходимости подробно останавливаться на выполнении описанных выше операций.

Ранее предполагалось, что ось х' направлена вдоль одной из сторон элемента. Иногда бывает полезно направить ее по линии пересечения плоскости треугольника с плоскостью, параллельной одной из координатных плоскостей. Так, например, если желательно направить ось х' вдоль горизонтальной стороны треугольника (т. е. параллельно плоскости ху), можно поступить следующим образом.

Во-первых, направляющие косинусы v определяются по соотношению (11.25).

Матрица направляющих косинусов оси л: должна теперь иметь нулевую компоненту в направлении г, Таким образом, имеем

п. Л

Поскольку длина вектора равна единице:

(11.28)

а скалярное произведение векторов у,- и Vz должно быть равно нулю, можно записать

+ V, = 0. (П.29)

Эти два уравнения позволяют единственным образом определить вектор Vy. Наконец, как и раньше,

V=-fxXt) (11.30)

Еще один способ однозначного определения оси х' описан в гл. 14.

11.6. Некоторые практические примеры

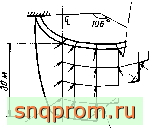
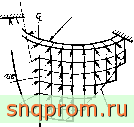
Первый пример посвящен расчету оболочки арочной плотины. Для расчета взята простая геометрическая конфигурация, показанная на фиг. 11,6, что позволило применить различные численные методы и провести сравнение с результатами экспериментов на моделях. Благодаря цилиндрической форме оболочки использовались прямоугольные элементы, хотя линия жесткого основания аппроксимировалась при этом довольно грубо.

Расчеты проводились для двух размеров элементов. Результаты расчета прогиба и напряжений на оси симметрии, приведенные на фнг. 11.7-11.9, показывают, что использование более

Действие давления воды в виде Ъснретных сил

Плоа <1олементы

!/оловые силы

Линия оаделни основания

Линия оаделни основания

Половые силы

Грубое разбиение Более мелное разбиение

Фиг. 11.6. Арочиая плотина как совокупность прямоугольных элементов.

		\ \\
		ft 1 1/

перемещений, мм

Фиг. 11.7. Арочная плотина. Горизонатальные перемещения центральной линии. □ решение методом конечных элементов (крупная сетка); V решение методом конечных влементов (мелкая сетка);---решение методом пробных нагрузок (USBR). (Коэффициент Пуассона vsOilS.)

Вершина плотины

сторона нижнего бьешс

Сторона верхнего Obeipa \

4,50 -ЗМ -г,Э -1.36 О.Эв о 0,9в ISB г.Э'1 З.Зг ti.SO 5.88 Напряжения в вертипальном направлении в сечении, , проходящем через вершину арни растяжение), Н/м'-Ю °

Фиг. 11.8. Арочиая плотина. Напряжения в вертикальном направлении на центральной линии.

□ решение методом конечных элементов (крупная сетка); А решение методом конечных элементов (мелкая сетка);---решение методом пробных нагрузок (USBR), (Коэффициент Пуассона у*=0,15.)

Сторона Верхнего бьесра

Сторона нижнего ioegia

		/ / / /
		1 1 1
н		1 1 1 1	□
и		\ \	а
		\ 1 N. У

-2,зи -1,ЭВ -0,38 О 0,38 Ш 2,34

Напряжения в гориоонтальном направлении В сечении, проходящем черев вершину арни (i-растяжение), Н/ 40

Фиг. 11,9. Арочная плотина. Напряжения в горизонтальном направлении (вдоль дуги арки) на центральной линии.

мелкого разбиения дает незначительное уточнение. Это свидетельствует о том, что физическая аппроксимация реальной формы плоскими элементами и математическая аппроксимация при использовании метода конечных элементов дают хорошие результаты. Для сравнения на рисунках показаны напряжения и прогибы, полученные другим приближенным численным методом.

<1

-\~-25,еж-

-39,8м-

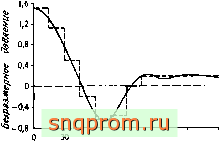
60 90

9,град

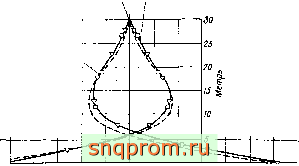
фиг. 11.10. Градирня [21]. Закон изменения давления по окружности.

-действительные значения;---предполагаеьые зчаченр*,

С помощью плоских треугольных элементов аналогично была рассчитана арочиая плотина двойной кривизны. Результаты показали даже несколько лучщую аппроксимацию [6].

Решение большого числа задач с треугольными несогласованными элементами Парехом [20] показало, что при одинаковом числе разбиений такие элементы приводят к лучшим результатам, чем согласованные треугольные элементы, использованные Клухом и Джонсоном [5]. Ниже приведены некоторые примеры расчета.

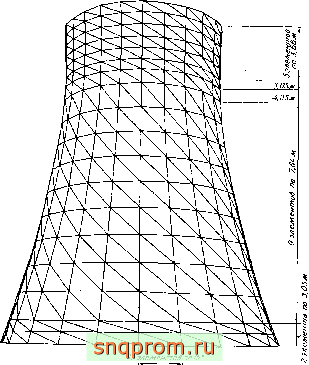
Градирня. Эта задача относится к классу осесимметричных. Очевидно, что более эффективно ее рассчитывать методами, изложенными в гл. 12 и 13. Однако здесь этот пример использует-

-30.5

-91,5 -3.56

				ТЬдщина
\\ \\ ц
If 1/					S. \ \ \ \ S
ll ll					\ ч \ \

3,56

7.13

т н/мю~~

30.5

-30.5

-91.5

		Толщина oSo/ючки 17.8сж
				-Толщина а5одочпи 1г,7сл1

0,03

0,15

0,09 0.12

Фиг. 11.12. Градирня, изображенная на фиг. 11.11.

0.18

0,21cM

а -мембранные силы прн 9=0*, Ы\.-тангенциальные силы, Л^г^мериднональные силы; б -радиальные перемещения при 9=0°; в, г -изгибающие моменты при 9=0 , Mi -тангенциальный момент, Mj -меридиональный момент. - метод конечных элементов;

---решение Албазини и Мартина.,

Фиг. 11,11. Градирня. Конечные элементы, метод конечнЕлх элементов;----решение Длбазнни и Мартнна.

1 ... 9 10 11 [ 12 ] 13 14 15 ... 27