Главная страница сайта
Российские промышленные издания (узловые агрегаты)
1 ...
7 8 9 [
10 ]
11 12 13 ...
27 необходимо использовать четыре постоянные, т. е. матрица [D] в этом случае имеет вид
[D] =
О. О
О О
о., J
(10.9)
Как показали Тимошенко и Войновский-Кригер [1], эти величины можно связать с соответствующими упругими постоянными материала, но удобнее оставить их именно в такой форме, так как теория пластин часто используется для расчета ростверков). В таких случаях эти постоянные должны отражать свойства ростверков. Ясно, что если материал обладает анизотропией общего вида, то в матрицу входит самое большее шесть постоянных, так как она всегда симметрична.
-4т
10.3. Условие непрерывности функции формы
Для обеспечения непрерывности функции w и угла наклона нормали на границе между элементами необходимо, чтобы w и dw/dn единственным образом определялись через заданные значения на этой границе.
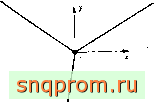
Рассмотрим фиг. 10.3, где изображена сторона 1-2 прямоугольного элемента. Направление нормали п фактически совпадает с направлением у, и, следовательно, необходимо, чтобы w и dw/dy единственным образом определялись значениями w, dw/dx, dw/ду в узлах, лежащих на этой стороне.
Следуя принципам гл. 7, можно записать, что вдоль стороны 1-2 прямоугольного элемента
W = Ai + А2Х + Азх'+ ... (10.10)
Фиг. 10.3. Требование непрерывности углов наклона.
= В, + В2Х + В,х'+
(10.11)
Число константа каждом выражении должно быть достаточным для того, чтобы выразить эти величины через параметры узлов на линии 1-2.
Так, например, если иа стороне имеются только два узла, можно допустить кубичный закон изменения w, так как в ка-
) Ростверком называется система балок, оси которых расположены в одной плоскости и пересекаются под прямыми углами. - Прим. ред.
ждом из узлов заданы значения dw/dx и w. Для величины dw/dy можно принять лишь линейный, т. е. двучленный, закон изменения.
Для того чтобы гарантировать непрерывность производной dw/dx в направлении у, нужно поступить аналогично.
Таким образом, вдоль стороны 1-2 dw/dy зависит только от параметров узлов линии 1-2, а вдоль стороны 1-3 dw/dx зависит только от параметров узлов 1-3.
Дифференцируя первую из этих величин по х, получаем, что на линии 1-2 dw/dxdy зависит только от параметров узлов линии 1-2. Аналогично находим, что иа линии 1-3 dw/dydx зависит только от параметров узлов линии 1-3.
В общей точке 1 возникает противоречие, так как в ней нельзя обеспечить выполнение равенства
дхду дудх
при произвольных значениях параметров в узлах 2 и 3.
Таким образом, если в узловых точках sadaubi только значения функции W и ее npouseodnbix, то функции формы, удовлетворяющие всем условиям согласованности, нельзя npedcTaeuTb в eude полиномов [2].
Произвольные функции, удовлетворяющие всем условиям согласованности, которые построены по трем узловым параметрам, в угловых точках не будут непрерывно дифференцируемы, а их смешанные производные не будут совпадать. Некоторые випы таких функций рассматриваются во второй части этой главы [3-7].
Приведенные рассуждения относятся только к прямоугольному элементу. Ясно, что их можно распространить на случай, когда в точке 1 стороны смежных элементов пересекаются под произвольными углами.
Путь преодоления этого затруднения очевиден. Можно считать смешанную производную одним из узловых параметров. Для ансамбли прямоугольных элементов это удобно и вполне допустимо. Богнером и др. [8] были предложены и с успехом использованы простые функции такого типа.
К сожалению, не всегда возможно использовать их для узловых точек, в которых пересекаются под разными углами границы нескольких элементов (фиг. 10.4). Здесь условие непрерывности смешанной производной в нескольких ортогональных направлениях фактически требует задания всех вторых npou3eodHbix в такой узловой точке.
Это, однако, приводит к нарушению физических требований при скачкообразном изменении жесткости пластины от элемента к элементу, так как невозможно удовлетворить условию
равенства моментов, нормальных к границам между элементами. Тем не менее при расчете однородных пластин такой метод довольно успешно использовался [9-11].
Смит [9] исследовал эффект наложения таких условий сверхнепрерывности на несколько производных высших порядков.
Трудности отыскания функций перемеш.ений, удовлетворяющих условиям согласованности, привели к попыткам игнорировать условие полной непрерывности угла наклона при выполнении других необходимых критериев. Исходя из несколько наивного интуитивного представления, что выполнение условия непрерывности угла наклона в узлв-вых точках в пределе приводит к полной непрерывности, было построено несколько очень удачных элементов [12-15]. Отличными от использованных в гл. 2 и 3 средствами можно показать и доказать сходимость методов, основанных на применении некоторых таких Элементов [4, 16]. Более того, можно показать, что при определенных условиях решение будет мало отличаться от точного [4].
Простота и широкое использование таких элементов объясняют, почему они ниже рассматриваются так подробно.
НЕСОГЛАСОВАННЫЕ ФУНКЦИИ ФОРМЫ
10.4. Прямоугольный элемеит с узлами в угловых точках [12, 17, 18]
10.4.1. Функции формы
Рассмотрим прямоугольный элемент ijkl пластины, лежащей в плоскости X, у (фиг. 10.2). В каждой узловой точке вводятся перемещения (би), которые имеют по три компоненты: перемещение w в направлении г, угол поворота {вх)п вокруг оси х и угол поворота {Qy)n вокруг оси у.
Перемещения узловой точки определяются соотношением (10.4), а перемещение элемента записывается, как обычно, в виде вектора, содержащего все (в нашем случае четыре) узловые перемещения:
5г
Фиг. 10.4. Уз.ты, в которых сторо ны смежных элементов имеют про нзвольные направления.
{6Г =
(10.12)
Для определения функций формы по двенадцати параметрам удобно использовать полиномы. При этом в полном полиноме четвертой степени необходимо опустить часть членов. Выражение
т = а1 + а2Х + азу + а^х^ + а^у + а^у' + щх? + а^-у +
-f OgXi/S + a.of/+ а„А + ai2Xi/3 (10.13)
имеет определенные преимущества. В частности, вдоль любой линии X = const или у = const перемещение w будет изменяться по кубическому закону. Все внешние границы и границы между элементами состоят именно из таких линий. Поскольку полином третьей степени единственным образом определяется четырьмя постоянными, перемещения вдоль границы однозначно определяются значениями перемещений и углов наклона в узловых точках на концах этой границы. А так как для смежных элементов значения на концах границы одинаковы, вдоль любой границы между элементами функция w будет непрерывной.
Можно заметить, что градиент w по нормали к любой границе изменяется вдоль нее по кубическому закону (например, dw/dx вдоль линии л: = const). Так как на таких линиях заданы только два значения угла наклона, то полином третьей степени определяется неоднозначно и в общем случае угол наклона может оказаться разрывным. Таким образом, эта функция является несогласованной.
Постоянные ai - an определяются из системы двенадцати уравнений, связывающих значения w и углов наклона в узловых точках, которые получаются в результате подстановки координат этих точек. Например,
w, = ai+ axi +щу,+ ит. д., (), = 9*= 2 + ит. д.,
Эти двенадцать уравнений можно записать в матричной форме: {бГ = [С]{а}, (10.14)
где [С] -матрица размерности 12X12. зависящая от узловых координат, а {а} - вектор, содержащий 12 неизвестных постоянных. Обращая систему (10.14), получаем
{а} = [С1-{бГ. (10.15)
7 Зак. 613 .
Это обращение можно выполнить с помощью ЭВМ или алгебраически, если желательно получить матрицу жесткости или Другие матрицы в явном виде. Так было сделано Зенкевичем и Ченгом [12].
Выражение для перемещений внутри элемента теперь можно записать в стандартной форме:
где
{?} = а; = [Л^]{бГ = [Р][С]-{бГ. (10.16)
[Р] = {1, X, у, х^, ху, у^, х^у, ху у^, х?у, V).
В явном виде это выражение получено Мелошем [17]. Приведенные выше соотношения просто записать в нормализованных координатах, введенных в гл. 7. В результате для любой узловой точки имеем
[iV<] = Y [do + 1)(Чо + I) (2 + Ь +110 - 1 - Ч\
где
Н(1о+1)(11з+1)Мть-1)],
(10.17)
с
It,
т1о = Л-11;-
Выражение для матрицы [В] получается непосредственно из соотношения (10.13) или (10.17) с использованием (10.6). Поскольку
Г -204 - бал: -2а^у - 6a jci/
{е} = < - 2аб -2а^х - боюг/ -6012*
+4а5л: + iay -f 6ai,*H6ai2
можно записать {е} = [QJ{a} =iQ] [С] {F и, следовательно, IB] = [Q1[C]-, где
. (10.18)
[Q] =
0 0 0 -2 0 О - 6л; ООО 00-2 О LO О О 0 2 О О
Интересно отметить, что выбранная функция перемещений до-пуска-ет существование состояния постоянной деформации (кривизны) ) и тем самым удовлетворяет критерию сходимости, сформулированному в гл. 2.
10.4.2. Матрицы жесткости и нагрузок
Процесс построения этих матриц стандартен, поэтому излишне излагать его подробно.
Из соотношения (2.10) можно получить матрицу жесткости, связывающую узловые силы (поперечная сила и два момента в каждом узле) с соответствующими узловыми перемещениями:
(10.20)
Подставляя сюда (10.18) и считая толщину t постоянной внутри элемента, получаем
{k]=\\[BY[D][B]dxdy.
да (10.18) и считая тол1 случаем
[k\=={[CTT{\\[QY[Dm\dxdy)[C]-\ (10.21)
Члены, не содержащие х и у, вынесены из-под интеграла. Если толщина t постоянна, то интеграл легко вычисляется точно после выполнения умножения под знаком интеграла.
Для ортотропного материала явное выражение для матрицы жесткости [k] приведено в табл. 10.1.
Соответствующая матрица напряжений для внутренних моментов приведена в табл. 10.2.
Внешние силы, обусловленные распределенной нагрузкой, можно распределить по узлам в зависимости от расположения участков приложения нагрузки. Однако более логично и точно для распределения по узлам внешних сил использовать снова соотношение (2.9).
Если в направлении w действует распределенная нагрузка с) на единицу площади элемента, то из соотношения (2.11) следует, что вклад этих сил в каждый из узлов выражается в виде
{F}l-\\\Nfqdxdy, (10.22)
или вследствие (10.15)
{F}\ {- [СГТ \ \ [Pf q dx dy. (10.23)
) Если постоянные а-, - an равны нулю, то деформации постоянны. С помощью формулы (10.13) можно найти соответствующие {б} . Так как между {6} и {а) существует однозначное соответствие, то такое состояние является единственно возможным. При этом предполагается, что матрица [С] существует. Обращение алгебраическим путем доказывает, что матрица [С] никогда не бывает сингулярной.
Таблица W.I
Матрица жесткости для прямоугольного элемента (фиг. 10.2, материал ортотропный)
Матрица жесткости
где
о о
о
р-2 =
О
5 -30 О
30 О -15
О О
10 -15 О
Симметрично
О 0 0 10 -30. о
Симметрично
60 -30 20 О
О О
ООО о о 0
Продолжение табл. 10.1
30 -15
15 -30 О
-15 -30 15
о о
о
-15 О
о -15
О О
О 15 О О О О О
30 15-15 30
О
О
Симметрично
О
15 О
0 0 30
О О -15 О
О О -15 15 О
О -30 -15 О -30 О 15
О -15 0 0 ООО
О О О О 15 О
15 О О -15 -15 О
84 6 8 -6 О 8
ООО
О г О О
0 0/0
о о о ;
где I-
-1 О О О 26 о О О 2я
Интеграл (10.23) тоже легко вычисляется. Заметим, что в общем случае все три компоненты внешней силы в каждом узле отличны от нуля. При простом распределении внешней нагрузки между узлами этого бы не было. Вектор узловых сил при действии равномерно распределенной нагрузки приведен в табл. 10.3.
Если в пластине существуют начальные деформации, то вектор узловых сил, обусловленных начальными деформациями и начальными напряжениями, находится аналогично. В этой связи необходимо заметить, что начальные деформации, например вызванные нагревом, редко влияют на кривизну. Обычно
в
а
Si 11 II
to to
Q i a. o.
q .5.
!M tr>(D
q о 9
CD CO
I I
q a.
q a.
Таблица Ю.З
Матрнца сил для прямоугольного элемента, изображенного на фнг. 10.2, при действии равномерно распределенной нагрузки д
\Fi i Fbyl
в пластине дополнительно возникают деформации в ее плоскости, и в целом поведение пластины можно изучить, решая наряду с задачей изгиба задачу о плоском напряженном состоянии.
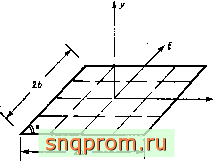
10.5. Четырехугольные и параллелограммные элементы
Четырехугольный элемент нельзя просто получить из прямоугольника. Можно было бы использовать преобразование координат описанного в гл. 8 типа, ио, к сожалению, в этом случае нарушается критерий постоянства кривизны. По-видимому, такие элементы обладают плохими свойствами. Используя только функции от и ti, лишь для параллелограмма можно удовлетворить критерий постоянства кривизны.
Такой элемент предложен в работе [12], а матрицы жесткости построены Дэйвом [14].
Нескольхо другая система функций формы предложена Аргирисом [15].
X, Г)
Фиг. 10.5. Элемент в форме параллелограмма и косоугольные координаты.
Для параллелограмма (фиг. 10.5) локальные координаты можно в явной форме связать с глобальными:
x - у ctgg а
у cosec а
(10.24)
что позволяет получить все характеристики элемента.
10.6. Треугольный элемеит с узлами в углах
10.6.1. Функции формы
На первый взгляд может показаться, что совершенно так же, как и в предыдущем разделе, в качестве функции формы можно использовать полином. Поскольку в этом случае задается только девять независимых перемещений, в полиномиальном разложении необходимо оставить девять членов. Однако полный полином третьей степени содержит десять членов [выражение (10.13)], и вопрос о том, какой именно член следует опустить, приходится решать произвольно. Для сохранения некоторой симметрии полинома можно, например, оставить все десять членов, а Чтобы свести количество неизвестных к девяти, приравнять два коэффициента (например, положить а& = кд). Было рассмотрено несколько различных вариантов. Однако при этом появляется другая, более серьезная проблема. При определенной ориентации сторон треугольника матрица, соответствующая матрице [С] системы уравнений (10.14), становится сингулярной. Это, например, происходит, когда две стороны треугольника параллельны осям XV.
Указанные трудности можно обойти, если воспользоваться описанными в гл. 8 L-координатами. Для треугольников это вполне естественно.
Как и раньше, будем использовать члены полиномиального представления. Отметим, что в L-координатах они имеют несколько необычный вид. Например, выражение
a,L, + 02-2 + Оз-з представляет собой полный линейный полином, а выражение
содержит все шесть членов полного квадратичного полинома (включая линейные члены).
Кубичный полином содержит десять членов, представляющих собой различные произведения третьей степени по координатам
Ll Ll Ll L\L2, L\U, lIU, ULl, UU, Ul], L1L2L3.
Для элемента с девятью степенями свободы можно использовать любую комбинацию из перечисленных членов, содержащую только девять независимых функций и удовлетворяющую критерию постоянства кривизны. На фиг. 10.6 показаны некоторые важные функции этого класса. Первая из них (фиг. 10.6, а) является одной из трех функций, описывающих перемещение пластины как жесткого тела.
Функции типа LiLa (в кубичном разложении их шесть) сходны (но не совпадают) с функцией, изображенной на фиг. 10.6, б.
Наконец, показанная иа фиг. 10.6, в функция L1L2L3 является чисто внутренней формой: во всех трех узлах значения функции и углов наклона равняются нулю. Такая функция оказывается полезной для неузловых парамет15ов, но не может использоваться самостоятельно, так как она не выражается через значения переменных в узлах. Ее можно с любым множителем добавить к другой основной функции формы.
Таким образом, особый интерес представляют функции второго рода. Они соответствуют нулевым значениям w во всех угловых точках и, кроме того, нулевому значению угла наклона вдоль одной из сторон. С помощью линейной комбинации двух из них (например, lILi и lILi) можно приписать любые значения углам наклона в направлениях х и у в одной узловой точке при нулевых значениях остальных углов наклона.
Однако для большей общности будем рассматривать формы типа
LiLs + cL\LiLb
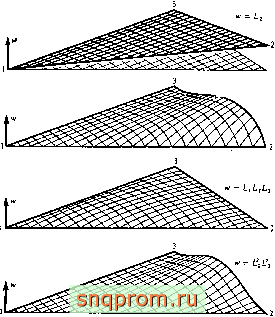
Фиг. 10.6. Некоторые основные полиномиальные относите.тьно /.-координат
функции.
(так как последнее слагаемое не изменяет углов наклона в узлах).
Поскольку кривизна описывается только этими формами, необходимо, чтобы с помощью линейной комбинации шести таких функций можно было получить любые произвольные значения кривизны во всех точках элемента при нулевых значениях w в узлах. Алгебраически это означает, что выражение
A,l,L2 + A2L2U+ ... +A,lI
при любых значениях коэффициентов А должно иметь вид
Bi {lIU + CL1L2L3) + Bi {l\L2 -f cULiU) + ...
при соответствующих значениях шести постоянных В. С помощью некоторых алгебраических преобразований можно показать, что это возможно только при с = 1/2. Следовательно, при
построении функций формы функция, изображенная на фиг. 10.6,6, является одной из основных.
Таким образом, перемещения пластины можно представить в виде
W = p.Z + + Рз.. + Р4 (ii. + i .2з) + + ... +P,(Z.?L3+ а) (10.25)
и после подстановки узловых значений
определить постоянные, а следовательно, и функции формы.
Окончательно функцию формы для первого узла с помощью определений, введенных в гл. 7, можно записать в виде
h (Z,?Z,2 + J LiL2L - bi [UL\ +1 LiUL Сэ {l\L2 + J Z Z,2L3) - C2 [UL\ + LyUL
(10.26)
где
Ь1=Уг - Уз, с, = лгз - x:2 и т. д. Остальные две функции для узлов 2 и 3 получаются циклической перестановкой индексов 1-2-3. Элемент, характеризуе-
мый такими функциями, впервые был рассмотрен в работе [4].
10.6.2. Матрицы жесткости и нагрузки
Для определения деформаций [равенство (10.2)] и матрицы [Bi] из (10.6) необходимо определить вторую производную от [Л^].
При этом появляется необходимость дифференцирования по декартовым координатам. Это нетрудно осуществить, имея в виду, что
д dLj. д I дЬг д , дЦ д
д дЦ
дх дЦ дх дЦ дх dL, 1
=-ж(*.11Г + *аС + з17)ит. Д. (10.27)
В /--координатах все выражения остаются полиномами, и поэтому их легко проинтегрировать с помощью общей формулы (7.34) гл. 7. Окончательные выражения для матриц жесткости и нагрузки довольно громоздкие; они приведены в работе [19].
Однако, как подчеркивалось в гл. 8, проще предусмотреть в программе численное интегрирование. Так как в матрицу жесткости входят только квадратичные члены, интегрирование по треугольнику будет точным при использовании всего лишь трех точек (см. табл. 8.3, гл. 8) и время численного интегрирования почти не отличается от времени расчета выражений при точном интегрировании.
В матрицу напряжений входят моменты, которые изменяются линейно. Однако, так как не все кубичные члены входят в функцию формы, они аппроксимируются плохо. Обычно моменты вычисляются только в центрах тяжести и результаты сглаживаются усреднением узловых значений,
10.7. Сходимость при использовании несогласованных элементов
При использовании двух типов элементов, описанных в предыдущем разделе, нарушаются условия непрерывности угла наклона н, следовательно, удовлетворяется только приближенно принцип минимума полной потенциальной энергии. Однако в следующем разделе будут приведены некоторые результаты, демонстрирующие практическую точность результатов, полученных при использовании этих элементов. Может возникнуть вопрос, всегда ли при уменьшении размеров элемента решение будет сходиться к точному? Хотя этот вопрос чисто теоретический, он нуждается в ответе.
Для прямоугольных элементов Вальц и др. [16], рассчитывая методом конечных элементов однородную пластину и сравнивая алгоритм с приближенным решением дифференциальных уравнений, установили, что сходимость гарантирована всегда. Однако распространять эти выводы на другие случаи нет никаких оснований.
Айронс [4] также показал, что использование простого треугольного элемента позволяет получить решение, сходящееся к точному, если сетка элементов образована тремя системами эквидистантных параллельных линий.
Использованный критерий проверки весьма прост. Если при помощи большого числа элементов можно точно воспроизвести любые состояния постоянной кривизны, то при предельном разбиении пластина ведет себя в соответствии с физическими законами для бесконечно малого элемента. В противном случае сходимости не будет.
Применение этого критерия показало, что если для получения треугольников используются две диагонали параллелограмма [фиг. 10.7 (4Х4В)], то ошибка в перемещениях составляет около 1,5%. Таким образом, несогласованный треугольник позволяет получить решение, сходящееся не к точному, а к неко-
торому другому, отличающемуся от него в пределах указанной ошибки.
Аналогичный критерий был применен к несогласованному прямоугольному элементу, что позволило впервые доказать сходимость для такого элемента [4].
В большинстве практических инженерных расчетов точность, достигаемая при использовании несогласованного треугольного элемента, оказывается вполне приемлемой. Чаще всего такие
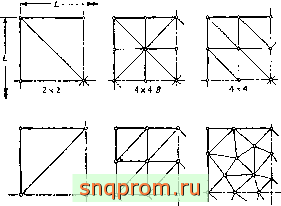
А Лк4 А Нерегулярная сетш
Фиг. 10.7. Квадратная пластина. Разбиение иа треугольные элементы.
треугольники дают лучшие результаты, чем эквивалентные согласованные элементы [4]. Это объясняется, по-видимому, тем, что решение в этом случае не обязательно удовлетворяет полученным в гл. 2 энергетическим ограничениям и большее число степеней свободы позволяет найти наилучшую форму.
При построении несогласованных элементов требовались непрерывность прогиба W во всех точках на границе между элементами и совпадение углов наклона в общих узлах. Это всегда приводило по крайней мере к кубическому закону изменения ш. Если несколько ослабить какое-либо из этих требований, то появляются интересные возможности. Например, можно показать, что для треугольника с шестью узлами, в качестве шести степеней свободы которого приняты значения ш в угловых узлах и значения нормальной производной dwjdn в дополнительных узлах, определяется полный квадратичный полином. В результате получается простейший возможный элемент для
задач об изгибе с постоянными моментами и кривизной, эквивалентный треугольнику с постоянной деформацией.
Такой элемент недавно был построен Морли [29]. Он показал, что, несмотря на достаточно очевидное нарушение непрерывности, полученное при использовании этого элемента, решение сходится и сопоставимо по точности с решением, полученным при использовании рассмотренных здесь более сложных треугольников.
В качестве упражнения читатель может получить матрицу жесткости для этого элемента.
10.8. Примеры
10.8.1. Прямоугольные элементы
Для иллюстрации точности и ожидаемой скорости сходимости была составлена программа расчета с использованием функций перемещений, определяемых выражением (10.13), и по ней просчитано несколько простых тестовых задач.
Квадратная изотропная пластина. На фиг. 10.8 в виде графиков представлены результаты расчета квадратной пластины
ПрогиВш W
изгибающие моменты
Фиг. 10.8. Квадратная пластина с защемленными краями. Равномерно распределенная нагрузка q. Квадратные элементы.
-- решение методом конечных разностей при сетке 15 X 15 (Саувелл, 1958)- о метод
конечных элементов, сетка 6X6; Д метод конечных элементов, сетка 4x4; о метод ковеч-вых элементов, сетка 2X2.
С защемленными краями, находящейся под действием равномерно распределенной нагрузки.
Результаты соответствуют разбиениям всего лишь на 2X2, 4X4 и 6 X 6 элементов, но точность и сходимость убедительны.
При любом количестве элементов линейное распределение моментов, как и ранее, близко к точному.
Еще более удивительные сходимость и точность демонстрируются в Табл. 10.4. В этой таблице сравниваются перемещения центра пластины прн действии сосредоточенной и распределенной нагрузок для различных условий закреплений сторон. При разбиении 8X8 элементов максимальная ошибка составляет ~3%. Для-всех случаев разбиения решение сходится.
Таблица 10.4
Перемещения центра квадратной пластины, подсчитанные при различном числе разбиений (прямоугольные элементы)
Разбиение | Общее количество узлов | Свободно опертая пластина | Защемленная пластина |
равномерно распределенная нагрузка а | сосредоточенная нагрузка | равномерно распределенная нагрузка а | сосредоточенная нагрузка Р |
| | 0,003446 | 0,013784 | 0,001480 | 0,005919 |
| | 0,003939 | 0,012327 | 0,001403 | 0,006134 |
| | 0,004033 | 0.011829 | 0,001304 | 0,005803 |
12X12 | | 0,004050 | 0,011715 | 0,001283 | 0.005710 |
16X16 | | 0,004056 | 0,011671 | 0,001275 | 0,005572 |
Точное реше- | | 0,004062 | 0,01160 | 0,03126 | 0,00560 |
ние (Тимо- | | | | | |
| | | | | |
для равномерно распределенной нагрузки q;
*макс в
3=1 для сосредоточенной нагрузки Р, приложенной в центре пластины [20], макс £)
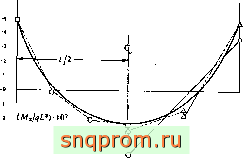
Коисольиая пластина. На фиг. 10.9 показаны перемещения в такой же пластине, но закрепленной консольно. Сравнение с другими численными решениями и экспериментальными данными снова демонстрирует высокую точность метода.
Опертая по углам пластина [12]. Квадратная пластина, опертая по углам, исследовалась различными экспериментальными н приближенными аналитическими методами. В табл. 10.5 результаты решения методом конечных элементов сравниваются с некоторыми другими приближенными решениями. Даже в том

-т-О
- 0,125 wDlqL*
Проги&1 вдоль линии А-А
-0,130
Эо,135 wD/qL*
/Jposuiii на свободная/ краю В'В
Фиг. 10.9. Нагружеиие равномерно распределенной нагрузкой q квадратной
консольной пластины. Д метод конечных элементон, сетка 3 X 3; □ метод конечных разностей, сетка 5X5 (Лнвси и Бирчелл, 1956); о экспериментальные результаты (Дэлли, 1948).
случае, когда наличие концентрации напряжений в узлах создает определенные трудности, ясно видно достаточно хорошее совпадение результатов как по перемещениям, так и по напряжениям.
10.8.2. Треугольные элементы. Квадратная изотропная пластина
Для иллюстрации сходимости снова рассмотрена квадратная пластина. Теперь она различным образом аппроксимируется треугольными элементами. В одних случаях они получены на
Таблица 10.5
Опертая по углам квадратная пластина (точка 1 - середина стороны пластины; точка 2 - центр пластины)
| | Точка 1 | Точка 2 |
ш | | ш | |
Метод конечных | | | | | |
| | | | | |
| | | 0,0126 | 0,139 | 0,0176 | 0,095 |
| | | 0,0165 | 0,149 | 0,0232 | 0,108 |
| | | 0,0173 | 0,150 | 0,0244 | 0,109 |
| | 0,0180 | 0,154 | 0,0281 | 0,110 |
Ли и Баллестероз | | 0,0170 | 0,140 | 0,0265 | 0,109 |
Множитель | | | qiyo | qL |
основе прямоугольной сетки, в других - совершенно нерегулярно. На фиг. 10.7 показано несколько способов разбиения, а на фнг. 10.10 представлены перемещения, определенные при различных краевых условиях и нагрузках. Как и ранее, точность и сходимость по перемещениям оказываются хорошими (хотя, возможно, и несколько хуже, чем при использовании прямоугольных элементов).
На фиг. 10.11 показано изменение изгибающих моментов вдоль оси симметрии пластины. Средние величины моментов хорошо согласуются с точными. Однако в этом случае уже нельзя сказать, что линейный закон распределения напряжения наилучшим образом согласуется с реальным. Поэтому в практических целях рекомендуется вычислять напряжения (моменты) в центре тяжести элементов.
Пластина с центральным круглым отверстием. Хотя эта задача и не имеет точного решения, она приведена для того, чтобы продемонстрировать, как с помощью треугольных элементов легко рассчитывать пластины произвольной формы с любыми отверстиями.
На фиг. 10.12 показана использованная сетка и нанесены линии равных прогибов ш. На фиг. 10.13 линии равных углов наклона сравниваются с экспериментальными результатами, полученными методом Муара. Расхождение не превышает ошибки эксперимента.
1 ...
7 8 9 [
10 ]
11 12 13 ...
27

