Главная страница сайта  Российские промышленные издания (узловые агрегаты) 

1 ... 3 4 5 [ 6 ] 7 8 9 ... 14

Таким образом,

			sin3
В		cosa	- sina cos 3
		sina	cosa cos 3

(3.22)

Проекции вектора J2 на связанные оси имеют вид

щ		а
щ

(2.23)

Матрицу получаем, рассуждая аналогично.

1. Проекции единичного вектора вдоль оси Of на оси системы АГ равны (0,0,1).

2. Проекции единичного вектора вдоль оси О'у на оси К' равны (sin, C0S7, 0).

3. Проекции единичного вектора вдоль оси О'х на оси К' равны (cos3 C0S7, - cos3sm7, sinjS).

Поэтому

5n =

cos3cos7 -cos3sin7 sin3

sin 7 C0S7 0

(3.24)

Получим выражения для обобщенных сил Qa, Qp, Qy, которые потребуются в дальнейшем при рассмотрении движения ротора. Для этого воспользуемся соотношением, следующим из определения обобщенных сил:

Мхх + МуЩ + М,Пг = Qaa + Оф + Qyy,

и подставим в него полученное выше выражение для О.. Тогда получим искомую связь

Qa Qp

1 о о

о cosa sina

sin3 -sinacos3 cosacos3

(3.25)

Для дальнейшего изложения введем цилиндрические системы координат: а) С с координатами z, г, tp: х = rcosip; у = rsinip и б) С с координатами f, р, ф: = рсовф; т? = рвтф. Найдем связь координат точки в этих системах. 102

Уравнение (3.20) запишем в виде

		г cos -
р sini		г simp -
Г

или развернуто

г COSVJ = Хо+ Р cos3cos(i + 7) + f sin;

г sin(/>= Уо + p[cosasin ( + 7)+ sinasin3cos(i + 7)] -f sinacos; (3.26) z = Zo + p[sinasin( + 7) - cosasin3cos(> + 7)] + f cosacos3.

В дальнейшем будем считать перекосы и смещения системы малыми, т.е. мало значение = тах( а|, 8), а смещения Хо, Уо, малы в сравнении с М = max(l/2*, z*) (i?*,z * - номинальные значения координат центра шарика), что равносильно малости значения Сх = maxOxol, \Уо\, zol)/A/. Пренебрегая членами порядка выше первого по ва, ех, решаем уравнения (3.26), из которых следуют соотношения

f = Z- Zo + riifi), р= г- р()- z?(vJ);

Ф = ч>-у -izU<fi)+ рШ, где

?((/>) = -asin(/>+ Pcosifi, (ifi) = -psimp- acosip; v(ip) = XoCOS(/> + Уо sintp,p(ip) = joCOS(/> - Xo&inip.

Выясним геометрический смысл полученных соотношений. Рассмотрим рис. 3.6. Точка М имеет цилиндрические координаты z, г, ip, декартовы координаты X = rcosip; у = rsinip,z. Единичные векторы вдоль осей О', (Л\, обозначим е^, е^, , а аналогичные векторы вдоль осей неподвижной системы координат обозначим е^, у, z-Третья строка матрицы S составлена из проекций вектора на оси системы К, поэтому с точностью до ва

Cf = -Р^х - аеу + Сг. Координата точки М по оси р равна

проекции вектора О'Л/ - ОМ - ОО на ось Of, т.е. скалярному произве-

дениюОМ и Cj.:

Ри& 3.6

(3.27)

(3.28)

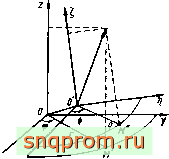
f = [(х-Хо)ех + (у- Уо)еу + (Z - Zo)ez, ] = 3(х -Хо) - а{у - у о) + ; + Z-Zo=Z-Zo+ г^(ф).

Это и есть первая формула из (3.27).

Координата р равна проекции вектора О'М на плоскость f = О или длине вектора OAf. Для О'М имеем выражение

0М = О-М-Г ef=(jf-Xo)e + (у -yo)ty + (z -Zo)ez -[z -Zo + ra()](e, + /Зех -ае,)я:=(х-лго -3z)ex + (у-д'о + Q:z)ej, -r?(i)ez,

О'ЛГ = r(exC0Sv5 + ej,smtp) - [{xq + 3z)ex + (Уо - аг)еу + г|((/))ег].

Длина вектора О'М в линейном приближении равна сумме длин первого слагаемого и проекции второго слагаемого на направляющий вектор первого слагаемого: -

р = (?Л/ r-(jCo+ 3z)cos(>-(yo-az)sm(/> = r-H;v5)-zKv)-Справедпивость второй формулы также доказана.

Первая и вторая строки матри1Ц>1 S составлены из проекций векторов е^, е^ на оси системы К, поэтому

= exC0S7 + e,sin7 - €2(7); е„ = - exsin7 + e,cos7 - ег { (7)-

Проекция вектора О'М на ось О'О'г}) равна скалярному произведению векторов о1 и е^(е ). Используя выражение для О'М , получим в линейном приближении

= (rcos<-Xo -i3z)cos7+ (rsiuip-yo + az)sin7= rcos(v5-7)- i(7) - -Ж7),

T) s-(rcosi/->:o -3z)sin7+ (rsin7-j>o+ az)cos7 = rsin(i-7)--M(7)-zf(7).

Таким образом, вектор + е^т/ складывается из двух векторов: efl+ е 17 =г[е|Со<(-7)+ e sm(v> - 7)] + -ej[i(7)+ г|(7)]--е^[м(7)+ zf(7)]}.

Видно, что угол ф равен tfi - у плюс поправка, обусловленная вектором в фигурных скобках и равная проекции этого вектора на единичный вектор - esin((j - 7) + eT,cos(v5 - 7) (ортогональный первому слагаемому), деленной на г. Таким образом,

Рнс 3.7

т

V = V-,7+ ([-e5sin((p-7)+e cos(i-7)],

-ej[K7)+ zK7)]-e;,[M(7) + гГ(7)]}) = [K7)+4(7)]sin(.-7) -~ [ m(7) + zf(7)]cos(, t,) = + (>)].

Таким образом можно дать наглядное геометрическое обоснование формулам (3.27).

Будем считать, что геометрия дорожек качения колец в связанной цилиндрической системе координат задается формулой

Рт =Рг*т(М + (- 1ГРт{Фт)-(- 1Г{р^(Фт)--[т-Р4*т(Фт)]]

(3.29)

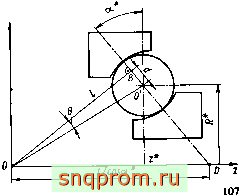
и представляет собой поверхность тора с отклонениями формы и размеров. На рис. 3.7 представлено сечение наружного кольца (т = 1) плоскостью Фт - const. Штриховая линия относится к кольцу с номинальной геометрией, а сплошная линия - к кольцу, имеющему отклонения геометрических параметров. Цилиндрические координаты центра кривизны сечения желоба в связанной системе координат в плоскости ф/ = const

Рт=Р2*т(<Р~Ут)+ (-) Рт(<Р-УтУ, fm =Р4*т{ч>-Ут)-

Введем малую величину бр (максимальное значение отклонения)

бр = max [ шах Ip/Cv)!]. 1</<6 0<1<2я

Цилиндрические координаты г^, z центра кривизны желоба в плоскости ifi = const в неподвижной системе координат можно определить из двух первых уравнений (3.27), для чего подставим в левую часть f = fm> р = РтИ решим эти уравнения относительно г, z. В линейном приближении по еа,ех, бр получим

Гт=Рт + fm(/)+ т%т{Ч>) = Рг*т + t Рт + pi-m(v-7m) +

Zm~tm + mo - Рт%т{ч>) = Рл*т + Pa * гг1ч> - Ут) +

(3.3oi

где р/ - отклонения геометрических параметров, обусловленные изготовлением (см. подразд. 3.1).

Расстояние v между центрами кривизны колец в плоскости tp = const вычисляем по формуле

v=V(zi-Zj) + (r,-rj)=f[ S (-l) z] +

m = 1,2

S (-D-r]} = Ь (-l) [p3.m+A.m(-7m) + 1=1.2 m = i,2

+ mo -(pS.m + (-1ГрПтШУ +{ 2 (-l) [p?. +

+ (-1ГРт + ft.mC-Tm) + ( 1) ;( -7m)+ m() +

>

(3.31)

Упругое сближение шарика с кольцами 5 =Р7 -Pi(<P-7i)-P2(<P-72)+v.

Вычислим V, используя выражение (3.31) и пренебрегая членами, содержащими квадраты отклонений геометрических параметров и смещений:

=*+,/-1Г[Р'2т(-7т)+(- 1) А;,(-7т) +

cosa* -

2 (-l) [p4.m(¥-7m) + m = 1.2

+ Zmo-(p?.m + (-l) pSa)lm(V)]

sina*,

(3.32)

где

V* = ((p? + p? + p5 -рЬ + (P? -P?)} = , cosa* = (p? + p? + p°-pO)/v*,

sina* =(p?-pg)/v*. Здесь V *, a* - расстояние между центрами кривизны и угол контакта в подшипнике без отклонений геометрических параметров, смещений и перекосов колец в состоянии предварительного натяга. При aj = а, + тг условимся называть углом контакта для всего подшипника величину а,.

Относительная погрешность, допущенная при переходе от (3.31) к (3.32), - величина порядка М/у*. Фактически значение этой величины 106

превышает ранее допущенные погрешности, поскольку отношение Mjv * ве-лико (для примера расчета из подразд. 3.2 М/у* =200). Упругое сближение шарика с кольцами вычисляем по формуле

s=5*+5, 5*=p?-p?-pS + v*;

5 = S (- l) [i; (i)cosa* -zosina* + 1т^тШ + m = l.2

+PV,P.7i,72), (3.33)

1 де 5* - упругое сближение в состоянии предварительного натяга;

р' = р'т + S [(cosa*-l)pw(¥-7m)+(-l) Ri*m(v-7m)cosa*-m= 1,2

I -(-l) pm(<-7m)sina*];

Im =P4 .m cosa* + (p°2 .m + ( !) Pm )sina*.

Модуль Im равен расстоянию от начала координат до линии контактов в подшипнике в состоянии предварительного натяга, поэтому h = h = (рис. 3.8).

Исследуем статическое комбинированное нагружение подшипника без отклонений в геометрии, исходя из выражения (3.31) для расстояния между центрами кривизны желобов.

Введем обозначения:

5z=Z2o-io; х-Хго-Хю; = У20-Ую

5a=a2-ai; 5 = 32-3i; Kv*) = 2(<р)- i() = SxCos-p + Vi

S(<p) = h(<P) - b(v) = - 5aSin( + Scosv.

Заменим величины p\*m, P%*m, входящие в формулу (3.31), Ha/?*,z , при этом будет допущена погрешность порядка v*/M (как правило, она не превышает 1 %):

\(ф)= [v*cosa* + Kv)+ z*k(}p)f +

Упругое сближение в сечении ifi = const вычисляем по формуле

Рис. 3.8

5(fp) = 5* - V* +v(.) = v 5* - 1 + [cosa* + Scosv) + SySiTup --z*(5asin. - Sgcosv)]* + [- sina* + 8+ *(5 sin - Scosj)] ,(3.34)

где 6*, 8x, 8y, 8z, z*, R* - безразмерные величины, равные соответствую щим размерным, отнесенным kv*. Потенциальная энергия в контактах| шариков с кольцами

где F(vy)- слагаемое в npaBoii части соотношения (3.34); iy - углова координата /-го шарика.

Пусть шарики расположены равномерно по окружности: ifij = io + + 27г(/ - 1)/Z и возможна полная разгрузка шариков. Тогда Z

П^Ко* S [8*-1+Fiipf)fe[8*-1 +Р(ф (3.35)

/= 1

Здесь в(х) - функция Хевисайда, определенная соотношением 1,х>0,

0,х<0.

Пусть к w-y кольцу приложены силы Fx,Fy,FzVi. моменты Мх,Му. Запишем уравнения равновесия

=(-i)-v*F = (-l)-v*F;

= (-1) у*г;

ЭП Э6

(3.36)

=(-1) а (-1) л/;с

= (-l) Qp= (-l) M.

Два последних приближенных равенства получены из (3.25).

Систему (3.36) решаем приближенно, так как она не имеет аналитического решения.

Рассчитаем матрицу жесткости подшипника при центральном положении колец. Для этого разложим выражение (3.35) по 8х,8у, 8z,8a, 8 до квадратичных слагаемых включительно, предполагая, что смещения и перекосы достаточно малы и в[8* -1 + F(ipf)] = 1 для любого/, т.е. все шарики нагружены. Выражение в фигурных скобках в формуле (3.34) равно I + Al + Аг, где

Al = 2[(8х + z*5)cosi + (8у -z*5a)sinv3]cosa* -- 2[Sz + R*(8aSinip-SpC0Sip)]ma*; Ai = [(8x + z*Sp)cos>p + (Sj, - z*5a)sini] + + [5г + Л*(5 51П¥ -5gCosv?)]. Используя формулу Тейлора, с точностью до квадратичных членов включительно получаем

Al Аг

(1+1 + 2) = Т~ г---8

6-(.)=[6-*-i.i.f-4-fr =

2S-* 26* 86*

4 6* 16 * 32

Тогда потенциальная энергия

п = а:о6* £

/ = 1

15 A\j

5 Al/ 5 Aij S a\j

4 6*

16 I*

Пусть шарики расположены равномерно по окружности, т.е. ср.=о+ 27J(/-1)/Z, Z>2. Воспользуемся следующими соотношениями:

(3.37)

S C0S(W45,) =

2 sin(.wv3/) = /=1

0,тФkZ, к- целое число, [Zcos(wio). = к2,; 0,тФ kZ, к - целое число, Zsin(W(po), w = kZ.

(3.38)

После преобразований получаем искомое выражение (в размерных переменных) для потенциальной энергии с квадратичной точностью

Z - zlLsina* + -(6j + 6) -2 s. 86 *v*

L 5Z , 3v

86*v<

;2 ; 2 *

+ 25sina*+/(5+5j)]}. (3 3

Таким образом, в линейном приближении система (3.36) уравнений равновесия сводится к линейной системе уравнений относительно 5, 5

Q О О О

О Q о -Сх(з О

О О Q О О

О -Схр О Са О

<*(3 О О О Са

5а 5/3

= (-1)

У

Отличные от нуля элементы матрицы жесткости

26*

г= Схх= Су у + --tqa*)cos2a*;

Са= Саа = С =Л'(1 + =Х(1 + -%q0)/

3v* Г 3v*

(3.40)

Q = 2l(l +-Ctqa*)sin*a*;

3v *

(3.41)

Схр - Cya -X(/cosa* + J(z *sma* - Л* cos a*) sin a*) =

3v *

= XZ(1 - tqa*tq0)cosa*; 3v*

d = /?*Cosa* -z*sina*; tq0 = .

n Z РИ- 3.8- В выражениях для жесткостей

присутствуют пропорциональные 5*/v* слагаемые, наличие которых вызвано тем, что были учтены значения квадратичного порядка при разложении К^р). Учет подобных величин для радиально-упорного под-шипника приводит к незначигельш.1м поправкам. Последние могут 110

оказаться существенными лишь в двух случаях: угол контакта близок к нулю (радиальный подшипник), угол контакта близок к 90° (упорный подшипник).

Пусть началом неподвижной системы координат (см. рис. 3.8) выбрана точка D пересечения линии контактов и оси симметрии подшипника.

P*Z R* PV.

Тогдаl = 0,d = R*/cosa*, С„ = -j - ,Схр

Сха = -

/?*tqa*.KaK

видно, в этом случае угловая жесткость меньше значения аналогичной величины из формулы (3.41) приблизительно в v*/5* раз (т.е. как правило, примерно на два порядка). Точка D называется полюсом подшипника и характеризуется тем, что угловая жесткость подшипника относительно этой точки аномально мала. Поэтому во избежание значительных перекосов следует обеспечить условия эксплуатации, в которых момент внешних сил относительно полюса равен нулю либо незначителен. Заметим, что если бы в формулах (3.41) для жесткостей не были учтены вторые слагаемые [порядка 5*/v*, обусловленные слагаемые Ail 2 и А]18 квадратичного порядка при разложении v((/>, то угловая жесткость относительно полюса была бы равна нулю.

Рассмотрим теперь задачу статики (3.36) в следующей постановке:

1) перекосы и смещения колец могут быть велики настолько, что может возникнуть разгрузка некоторых шариков;

2) потенциальная энергия вычисляется по формуле

П =Ко{у*Г^ Л5* - 1 + РШ 0[д*- 1 + Р{ур)Щ, (3.42)

которая получена из (3.35) в предположении, что2 °°. Пункт 1 фактически означает, что допускаются настолько большие смещения, что уже нельзя пользоваться уравнениями статики (3.40), верными в линейном приближении, однако величины Ва и Вх оказываются все еще малыми. Пренебрежем в выражении (3.34) для упругого сближения квадратичными членами (т.е. слагаемыми All, AllS, вклад порядка 5*/v*). Тогда выражение (3.42) для потенциальной энергии принимает вид

2п

/ [Лг + Axcosifi + Aysin(/>] 0(Лг +

+ A;xCOsv>+ Aysinifi)d>fi; Аг=5* - Szsina*;

* S0)cosa*, Ay = iSy - -L-SJcosa*.

Заметим, что выражения, стоящие в круглых скобках в формулах для Лд: и Лу, представляют собой х- и >-смещения внутреннего кольца относительно наружного в точке D. Введем переменную Л^- = >/л|~+~л| и преобразуем выражение для потенциальной энергии

2п

П = 4 0 / (Az + Arcosf 0(Лг + Л.сов^)) d,).

5 2.

(3.43)

Эта формула верна не только для подшипника с предварительным осевым натягом, но и для подшипника, который в начальный момент находится в состоянии предварительного касания, причем в последнем случае в выражениях для Ах, Ау, Лг следует положить а* = Uq.

Уравнения равновесия (3.36) в случае, когда потенциальная энергия определяется формулой (3.43), принимают вид

(-1) , =KoZIr

(-irFy=KoZIr

(8; cosa* +8/)cosa*

{6;COsa* - 6a/)cosa*

(-l) *Fz =KoZIzSma*;

(- l) Mx =KoZIr У-

(8/ + SxCo%a*)l

1 - COSip

-- / (Az + A;COSv>)0(Az + ArCOSip)dif. 2я Q 1

Из двух первых и двух последних уравнений следует, что

Fy = 0; My --

-Fr = 0.

cosa cosa*

т.е. поперечные моменты относительно полюса равны нулю. Таким образом, и в нелинейной постановке угловая жесткость относительно полюса равна нулю.

Разделив первые два соотношения на cosa*, возведя их в квадрат и сложив, получим

(Fi + F})/cosa* = (KoZIr)\

Обозначим Fr = V Fx + Fy радиальную составляющую силы. Тогда совместно'с третьим уравнением системы получим

F cosa* ArCOSVJ)COS0(Az + ArCOS<p)d.

K.Z 277

о

(3.44)

X 0(Az + ArCOSip)difi .

Из этих уравнений можно определить условия разгрузки шариков. Разгрузка начинается, когда Az + A-cosip принимает нулевое значение хотя бы при одном значении р. При Лг > > О значение указанной величины положительно, и разгрузка невозможна. Начальному моменту разгрузки соответствует Az = Л^. Подставив это соотношение в уравнения (3.44), имеем

F дз;2 2 Г 2 2

---f- = /(1 + cos) cosipdip =-ЛЗ;

KZco$a* 2я о 10я

= ;(1 + cos,pfd,p= АГ,

KZsina*

2п

откуда, исключая А получаем условие начала разгрузки шариков

5Fr Seir-fz (3.45)

cosa

sina*

Для доведения системы уравнений (3.44) до сравнительно простой расчетной методики введем следующие обозначения:

Az

л = V А|+Л>; X = arccos-,

л

F =

; 9г = arcsin

KZ F cosa*

O<0f <я/2.

Тогда система (3.44) в новых переменных принимает вид

Fosin0г= л' /,(х);

FoCos0/. = A3/z(x);

(3.46) 113

2-П

/(cosx+ smxcos(/>) 0(cosx +

+ sinxcosip)

COSip

где величины Ра,вр,Ко,2 заданы. Определим х из уравнения

СО%вр =-

которое следует из системы (3.46). Затем

[/(х)+ /Их)!

/л(х)-

(3.47)

(3.48)

Максимальную нагрузку Р^ах действующую на щарик, определяем по формуле

imax =Jo(Az + Л,) = /max(x);

/ш ах (X) = (COS X + sinx)VV/(x)+7?(x):

Из последнего уравнения следует, что cosx + sinx > О, т.е. О < х < Зл/4. Угол вр нагруженной зоны (угол сектора, который занимают нагруженные шарики) определяется формулой

27Г, 0<х<т/4,

2 arccos (- ctg х) = 27Г - 2 arccos (ctg х), 7г/4 < X < Зя/4.

Определим также минимальную нагрузкуР„ , действующую на шарик:

imin = о(Лг - Л,) в (Лг - Л,) = FI in(x);

/min(x) = (cosx - sinx) 0 (cosx - sinx)/V/(x) + /?(x)-

Минимальная нагрузка отлична от нуля при О < х < /4 и равна нулю при 7г/4 < X < 37г/4. В табл. 3.1 представлены значения вр, х, вр, 1, /ах тт-ПриХ37г/4

/л ~

1.07925 (Зя/4-х)

Ли ах ~

1,8856

(ЗтгМ-х)

Зависимости х (f) . -л (х). ах (х). щ in (х) всем диапазоне изменения вр их можно аппроксимировать следующими формулами:

Г 1,3420/г,О<61<О,515, Х(М = 3,4780/,-1,1, 0,515 <0/,< 0,648,

8,759 (вр - 7г/4) + ЗтгМ, 0,648 < 0 < 7г/4

(с погрешностью менее 3 %) ;

1,07925

/л(х) =

(с погрешностью менее 5 %);

1,8856

[1 + 0,132 + 0,288 (37Г/4 - х) (37г/4 - х) ]

шах

(Х) =

(Зя/4-х) (с погрешностью менее 2 %) ;

min(x) =2-/,(х),0<Х'

[ 1,364 - 0,262(х - 37Г/8)* - 0,186е-5

;7г/4

(с погрешностью менее 2 %).

При значениях х, больших 37г/4, задача не имеет решения. Исследуем задачу при х Зтг/4. При указанных значениях х угол зоны нагруженных шариков стремится к нулю, и интегрирование в (3.46) проводится по малой окрестности точки tp = О, где cosx + sinxcosip > 0. Эта окрестность тем меньше, чем значение х ближе к 37г/4. Если в первом интеграле (3.46) положим cos = i, то при X -*Зп/4, I/Iz 1. Тогда, как следует из (3.47), cosdp -* 1/л/2, твр -* 1/V2, и верно равенство

(-l) *F, р.

Это соотношение определяет максимально допускаемую радиальную нагрузку при заданной осевой

(-!) Fctgft*.

Решение задачи, в котором число шариков равно бесконечности, принадлежит Шовалю. Такое его изложение, хотя и отличается от классического, но, по нашему мнению, является более удобным, поскольку вход-, ной параметр 0р меняется в конечных пределах.

Перейдем к исследованию статического комбинированного нагружения подшипника с учетом отклонений геометрических параметров. Для оценки упругого сближения шарика в контакте используем формулы (3.33). Пусть углы перекосов, смещения и отклонения малы настолько, что нагружены все шарики. Тогда потенциальную энергию, запасенную в упругих контактах одного подшипника, вычисляем по формуле

0 = 4-0 i (5* + 5; )* /= 1

Таблица 3.1

eг lO,paд	X, рад
0,000	0,00	360,00	1,000	1,000	1,00000
0,300	0,04	360,00	1,000	1.060	0.93990
0,600	0,08	360,00	1,001	1,119	0,87950
0,899	0,12	360,00	1,003	1.178	0,81910
1,198	0,16	360,00	1,005	1.237	0,75880
1,495	0,20	360,00	1,008	1,294	0,69860
1,792	0,24	360,00	1,011	1.351	0,63870
2,087	0,28	360,00	1,015	1.407	0,57930
2,381	0,32	360,00	1,020	1,463	0,52050
2,672	0,36	360,00	1,025	1,517	0,46260
2,960	0,40	360,00	1,031	1.570	0.40570
3,245	0,44	360,00	1,038	1.622	0.35020
3,527	0,48	360,00	1,045	1.674	0.29620
3,803	0,52	360,00	1,053	1,723	0.24420
4,074	0,56	360,00	1,062	1,772	0,19460
4,338	0,60	360,00	1,072	1,819	0.14780
4,594	0,64	360,00	1.083	1,865	0.10450
4,839	0,68	360,00	1,095	1,910	0.06573
5,070	0,72	360,00	1.107	1,953	0.03274
5,283	0,76	360,00	1,121	1,995	0,00808
5,465	0,80	332,40	1,135	2,035	0,00000
5,612	0,84	307,40	1,151	2.072	0.00000
5,738 5,894	0,88	291,50	1,168	2.108	0.00000
	0,92	279,20	1,186	2.144	0,00000
5,949	0,96	268,90	1,207	2.179	0,00000
6,040	1,00	259,90	1,229	2,214	0,00000
6,123	1,04	251,90	1,254	2,248	0,00000
6,200	1,08	244,60	1.281	2,283	0,00000
6,272	1,12	237,90	1,311	2.318	0.00000
6,339	1,16	231,60	1.334	2,353	0.00000
6,403	1,20	225,80	1,380	2,388	0,00000
6,463	1,24	220,20	1.420	2,425	0,00000
6,521	1,28	214,80	1,465	2,462	0,00000
6,576	1,32	209,70	1,514	2,500	0,00000
6,629	1,36	204,70	1,568	2.539	0,00000
6,680	1,40	199,90	1,628	2,580	0,00000
6,729	1,44	195,10	1,695	2,622	0,00000
6,777	1,48	190,40	1,770	2,667	0,00000
6,825	1,52	185,80	1,854	2,713	0,00000
6,871	1,56	181,20	1,948	2.726	0,00000
6,916	1,60	176.70	2.054	2.814	0.00000
6,961	1,64	172,1	2,157	2,870	0,00000
7,006	1,68	167,40	2,313	2.930	0,00000
7,050	1,72	162,70	2,472	2.994	0,00000
7,094	1,76	157.90	2,657	3,065	0,00000
7,138	1,80	153,00	2,873	3,142	0,00000
7,183	1,84	148,00	3.129	3.228	0.00000
7,228	1,88	142,70	3,435	3,324	0,00000
7,273	1,92	137,30	3.808	3.432	0,00000
7,319	1,96	131,60	4,270	3,557	0.00000

Продолжение табл. 3.1

вр-\а ,рад	X. рад			тах
7,365	2.00	125.50	4.853	3.703	0,00000
7.413	2.04	119,10	5,611	3.876	0,00000
7,462	2,08	112,10	6,628	4,086	0.00000
7,512	2,12	104.50	8,053	4.350	0,00000
7,564	2,16	96,11	10,170	4.695	0.00000
7,618	2.20	86,58	13,590	5.170	0.00000
7,675	2,24	75,45	19.880	5.883	0.00000
7,733	2,28	61,78	34,390	7.122	0,00000
7,827	2,32	29,01	265,100	14,960	0.00000

Предположим, что б^/б* < 1 для любого /, и разложим выражения в скобках под знаком суммы в ряд по 5/5* до квадратичных членов включительно:

П = - 5** i (1 + 4

5 /=12

P*d*Z +

+ Р* 2

8 s*

Р (а*, /, 71,72) + I (-1) [Р„ (¥>/)cosa* -

ffl - j-

sina* + (ip)] j + <(l ,F(a*, p,-, 71,72) +

+ 2 (- l) * [u (cp/)cosa* -zsina* +/ (cp;)]j . (3.49)

Функция Pia*, ip, 7i, 72) дана в (3.33). Используя формулу (3.49), можно найти силу Р', действующую на /-Й щарик в окружном направлении, обусловленную отклонениями формы и размеров дорожек качения и радиальным смещением внутреннего кольца относительно наружного. Момент относительно оси Oz кольца равен Р'*. С другой стороны, этот момент равен - dU/dipi. Продифференцировав выражение (3.49) и учтя при этом только линейные (по отклонениям геометрических параметров и смещениям) слагаемые, получим

R * difij

R* d>Pi

Р'(а*,Pi, 11, У2) +

+ 2 (- 1)[v (ipi) cosa* +(ip,) ] m = 1. 2

* 1т=г,

+ (-1)

-cosa -

-(-1)

- SfSintj) cosa* - /(5q,cosv3j- + 5sinipj) ] .

(3.50)

Предположим, что кольца подшипника идеальны. Тогда в формуле остаются лишь слагаемые в последних квадратных скобках, и максимальное по tp значение силы

тах = V(5yCosa* - /SJ + (5cosa* +/5)

(3.51)

Предположим, как это было раньше, что шарики расположены равномерно по окружности: = ч>о + 2 7г(/ - 1)/Z, а их число превышает 2. Воспользовавшись формулами суммирования (3.38), получим

П = P*S*Z +РЮг + - . 1 Р (а*, 71,72)

46 * /= 1

-F*Z5,sina* + - [5cosa*+ /5] + [Scosa*-

- Z5J £> - 5,Z),sina* + Z(5cosa* + /5) + + 4 Z(5cosa* -/5J + ZSina*;

86< Dy

= 2/(a*, .p., 71,72) /= 1

COScpy

sinipy 1

(3.52) (3.53)

Таким образом, потенциальная энергия складывается из трех слагаемых, не зависящих от координат ротора, а определяемых только отклонениями геометрических параметров и углом поворота комплекта; линейного слагаемого F*Z5sina*; трех слагаемых, в которые входят обобщенные отклонения D,D D; последних трех слагаемых, представляющих собой потенциальную энергию (в квадратичном приближении) подшипника без отклонений формы и размеров, причем угловая жесткость относительно полюса равна нулю.

Используя выражение (3.52) и уравнения (3.36), условия равновесия запишем в следующем виде:

			0 -с,~
			-с^о				Щ
			0 0
			Q 0
							-Oleosa*
							-DyCosa*
= (-	1)	FzH-	-l) i*Zsma*
							-Dxl

(3.54)

где C Суд - жесткости, рассчитываемые по формулам (3.41) после

отбрасывания вторых слагаемых в скобках (т. е. величин порядка 5*/v*).

Наличие отклонений формы и размеров, обусловленных погрешностями изготовления, приводит к тому, что и при отсутствии внешних сил кольца смещаются друг относительно друга. Уравнения равновесия обладают свойством: если прые части равны нулю (если кольца идеальны и на них не действуют силы), то уравнения имеют тривиальное решение 5 = 5 = = 5 = 5q, = 5д = О, из которого следует, что смещения и перекосы внутреннего и наружного колец одинаковы. В матрице жесткости первая и вторая строки пропорциональны соответственно пятой и четвертой. Следствием этого, как и ранее, являются два уравнения

cosa*

F = 0; М^-

означающие равенство нулю поперечных моментов относительно полюса. Если ввести величины

5 = 5 +

oosa*

Sy - Sy -

oosa

соответствующие х- и д'юмещениям колец друг относительно друга в полюсе, то их вместе с 5 можно определить из системы (3.54):

°х =-~-

2 -

/oosa

Zoosa*

(3.55) 119

; (-l) F.+P*2sina*

-i-+

г sin a*

Для применения данньк формул к расчету конкретных подшипников получим выражения Dx,Dy, через разложение в ряд Фурье отклонений геометрии. В выражения (3.53), определяющие указанные величины, входят слагаемые вида [см. выражение (3.33) для/*]

cosiriipj)

, /=1,...,6;

п - целое число.

Воспользуемся комплексной формой представления отклонений формы и размеров в виде ряда Фурье (3.1) v

и вычислим

Qlnm = jP/(v/-r )e

(3.56)

Подставляя разложение /-го отклонения, получим

Использовав формулы суммирования (3.38) в комплексной форме

О, J # /-Z, г - целое число,

(3.57>

получим

G/ ;;,=2 C;t/exp

целое число. (3.58)

В этой формуле суммирование проводим не по всем цельпи к, а лишь вида tZ - п.

Полученное комплексное равенство эквивалентно двум вещественным: Z

со siriifij) sin(n/)J

2 k = tZ-n

(ky - tZipo)

(3.59)

Здесь д^;, b ! - амплитуды при косинусах и синусах порядка к в раз-ложешш /-Г0 отклонения в ряд Фурье; Re4, 1тЛ - соответственно действительная и мнимая части комплексного числа А.

Использовав выражения (3.59), можно рассчитать значения 3 3 /г. определенные формулами (3.53) :

= 2 /=1

+ (- (¥>/ -Tm)cosa* - (- (V. -y)sma*

= 2 /=1

PjjCOSifij

Pnj sinv)-

+ 2 /n= 1,2

COSiPf

sini.

(cosa* - 1)

Qmom

ReG(4+m)lm I G(4+,n)l/n 6(4 + m)07n

+ (-l) cosa* Ime(2+, )im + (-l) sina*

6(2 +m)om При к = tZ - I получаем

z z г

= 2 p cos</ --- 2 2 J cos(A:-y - tZ>po) [(cosa* -

-iHm + (-O cosa*a;t(2 + m) (-l) sma*aft (4 + m) 1 -sm(fc7m tZifio) [(cosa* - 1)Ь;/п + (- l) cosa*b;t (2+/n) -(-l) sina*6,(4 )}; (3.60)

/=1 w= 1,2 f L

-/ZvJo) [(cosa*-l)&fc + (-l) cosa♦ft;t(2 + m)-- (- 1)sina*6;t (4 +m) ] - sin(Tm - Zpo) [ (cosa* -- l)fl;t+ (-1) cosa*afc (2+m) -(-!) sina*a;fc(,+)]f ; (3.61)

cos[rZ(r -o)] [(cosa*-

- Oaz). + (- l) cosa*fl(,) ( ) ( D-sina*.,) (..j

1 ... 3 4 5 [ 6 ] 7 8 9 ... 14