Главная страница сайта  Российские промышленные издания (узловые агрегаты) 

1 2 [ 3 ] 4 5 6 ... 14

Я„ = 0,0718

15000. 2,r 10

6 = 0,238

13,29 10- (1 - 0,33) 15000 .(1-0,33)

26,59 2,1- 10 По формуле (2.12)

10- =

= 1,196 ГПа;

= 16 мкм.

tg2ai, = -

(16-2 - 10 ) .sin0,04

(16-2- 10)cos0,04-2-10 16/79 799,36

= - 0,033;

- 19968 - 4050 2wj*-0,033; -0,0167 =-0,95°.

Таким образом, большая ось эллипса повернута на 0,95° относительно оси кольца в ту же сторону, что и ось ролика.

Пример 2.3. Данные те же, что в примере 2.2, но без рыскания. Вследствие симметрии ш = 0; Rx = 2 10 мм; Ry = 16-79/(16 + 79) = 13,3 мм; R = RxRylix + + Лу) = 2 . 10 . 13,3/(2 10 + 13,3) = 13,25 мм; RyjRx = 13,3/(2- 10 ) = 6,65 X X 10~

Решение. По табл. 2.1 у = 85,8;* = 24,153; к/, = 0,28096; кр = 0,0705; kg = 0,23128. По формулам (2.16) - (2.18) а = 22,81 мм; b = 0,266 мм; = 1,17 ГПа; 5 = 15,5 мкм.

Для соприкасающихся цилиндрических тел = < ; / = 1, 2)

формулы для b и рополучаем при 7- > иэ (2.16) и (2.17) соответственно. В этом случае К D°°, Ry/Rx 0, kg °°,а^°°, К - 1. Сила Р связана с нагрузкой q = 7троЬ/2 на единицу длины области контакта формулой Р - 4qal3, Преобразование формулы (2.16) при 7 -> < дает

ь=1,бУ:ж:,

(2.21)

TpfiR-RiRil (Rj +Л2); Rl =Ri2, R2 =22. Подстановка в формулу Ро = 2q/ (nb) дает

Ро=0,4 s/qEjR. Формулу (2.18) при 7

°° приводим к виду 4а

(2.22)

(2.23)

TiE пЕ b

Это же выражение для 5 получается из (2.15) при Яд. х = j = 0,у^°° Распределение давления в контакте, согласно формуле (2.4), можно представить в виде

Р(х,у) = Ро{х) у/\-у^1Ь\х),

(2.24)

.р^(;с) = ро >А 1 -х'Ы'; Ь{х) =Ь Vl xVfl - переменные максимальное давление и полуширина области контакта в сечении х = const. При ос, фиксированных х и Ро из (2.21) получаем предельное распре-

д£ 1ение давления

(2.25)

2.2. КОНТАКТ УПРУГИХ ТЕЛ ПО УЗКОЙ ОБЛАСТИ

При расчете распределения давления в контактах двух упругих *л (в частности, шариков ипи роликов с кольцами подшипники каченш) тела в области контакта заменяют на упругие полупространства, ТоЕда задача определения давления сводится к двухмерному интегральному уравнению. Во многих практических случаях область контакта оказывается вытянутой в одном направлении. Таким свойством обладают контакты шарик - кольцо и ролик - кольцо. Но если в контакте шарика с кольцом давление определяют из задачи Герца, то в контакте ролик - кольцо давление найти сложнее, поскольку ролик в общем случае имеет криволинейный меридиан. При решении этой задачи пользуются методом плоских сечений, предполагая, что профиль давления в поперечном направлении представляет собой половину эллипса.

Область контакта (рис. 2.3, а) считается узкой, если ее характерный размер L в направлении оси Ох много больше характерного размера В в другом направлении {Оу). В этом случае полагают, что в каждом сечении X = const (рис. 2,3, б) происходит контакт двух цилиндров с радиусами Я\уТлК2у. Распределение давления в области S2:

р{х,у) = Ро{х) \П-у^Ь'(х), (2.26)

где максимальное значение давления ро (х) в сечении и местная полуширина Ь(х) области контакта определяются формулами (2.21), (2.22) для контакта цилиндров:

2iiR,

Hx) = 4/Si.

(2. 27)

Здесь <?(х) = яро (х)Ь(х)/2 - интенсивность распределенной вдоль оси Ох нагрузки, или площадь под графиком р{х, у) в сечеиии х = const,

2Е[ е\

е[ + е:

Riy Riy

Е; = -0=1,2);

1 -V:

Rly + R

В соответствии с (2.1) уравнение для давления в контакте имеет вид

2 pa,ri)didn

-fs(x.y) = wix,y).

= 5 + {х-Хо)в-

(2.28)

где S - суммарное перемещение тел в точке Хо первоначального контакта, равное сближению тел на бесконечности; fs (х, у) = fi (л; у) + /2 {х,у); fj{x,y) при / = 1, 2 - расстояние от поверхности /-го тела до касательной плоскости к телу в точкех; в - угол перекосг.

	V /77Z	а
				л

Рис. 2.3

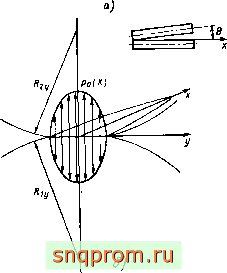
Подставив (2.26) в (2.28) с учетом (2.27) и приняв = О, получаем уравнение для q{x):

8 f J{x,%)qi%)d\ = yA.x,o\ (2-29)

1 /2

Границы л:-и / области контакта (см. рис. 2.3) заданы, если тела ограничены острыми кромками. Если же тела гладкие, то и х определяют из условий

.(.0=.(-)=0. (2-30)

Условие равновесия имеет вид

где Р - сила, сжимающая тела.

Величину входящую в J(x,), определяют по второй формуле

(2.27). Уравнение (2.29) - нелинейное одномерное интегральное с ней* вестными границами, для численного решения которого, наряду с асимптотическими методами, применяют итерационный (метод последовательны с приближений). Для этого на интервале [х; х*] вводят равномерную сет1 :у

Xi=x-+ (/-1)А, h=(x*-xyn, /=1,...,и+ 1,

и уравнения (2.29) - (2.31) приводят к виду

8Л + 1 (*-1) (Л) 4i

п + 1 S

I = 1

Ci Jji

п + 1

/= 1

Ci Qi = Р;

(2.32)

(2.33) (2.34)

() ()

где/=1.....n + \;qi =q (ki), J-fi = Ах ), = wixj,Oy, к - номер

приближения; Cj = c +i = 0,5; с, = 1 для 2</<и (формула трапеций).

При вычислении Jji используют значение <?/, полученное при предьщу-щем приближении, что позволяет рассматривать (2.32) как линейное уравнение. Сначала задают некоторые q и близкие значения х' их*. По

<?) вычисляют &Р^= й^Ч?;) и JJP. В и + 4 уравнения (2.32)-(2.34) входят и + 4 неизвестных: <?Р^(/= 1,..., и+ 1),х', х*, S. Значение S вычисляют из выражения для Ф^. При решении системы (2.32) - (2.34) находят qp\ увеличивая отрезок [х', х*] до тех пор, пока условие (2.34) не будет выполняться с определенной точностью (х~ уменьшают, ал;* увеличивают на значение шага А). Процесс обрывают при к = т, если q достаточно близко к q ~ Особенность задачи - необходимость вычисления син -гулярного интеграла. В уравнении (2.29), содержащем сходящийся двойной интеграл, при переходе ко второму интегралу при ? = О или f = О получаем расходящиеся одномерные интегралы. Можно воспользоваться непрерывностью по z интеграла

I{x.z)= f fqia х- о

1 - г

заменить его суммой типа (2.32) и перейти к пределу при А и z, одновременно стремящихся к нулю. Практически J-- определяют линейной экстраполяцией по двум значениям z = х^, где х - параметр настройки метода. Изложенный метод решения задачи полезен при расчете давления в

0,8 0,6 0,4 0,2 О

			А
			->

о

Рис. 2.5

Wx.MM

6(х),мм

8 16 х,мм

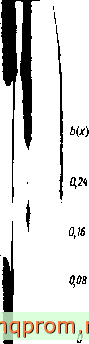
Рис. 2.4

0,3 0,2

0,1 О

			А

Рис. 2.6

контакте деталей сложной формы, которую вблизи точки первоначального контакта нельзя описать полиномом второй степени по л; и^. Такую форму имеют, например, профилированные ролики, применяемые в подшипниках букс и в опорах главного вала некоторых газотурбинных двигателей. Фогр-ма двухрадиусного меридиана ролика задается функцией

Ш, о)=<

а\ -\/ -{x-a-if, х>а, Ol -у/г' -(х+ Дг). х<-а.

где

а,=Ло[1-(1-)У1- а2=а(1--),

о Rl о

а, Ло и Г - параметры меридиана, составленного из трех сопряженных дуг окружностей.

На рис. 2.4 приведены зависимости от х полуширины b области кон-

такта такого ролика и внутретнего кольца подшипника 42726. Диамевр ролика = 32 мм, его длина / = 46 мм, Р= 15 кН, г = 0,4 мм, а = 20 мщ, радиус дорожки качения Ri = 79 мм, материал - сталь; кривая I - Rq = 65 м, кривая 2 - 80 м, кривая 3 - \0*м, кривая 4 - Ю^м.

На рис. 2.5 и 2.6 представлены зависимости от х интенсивности! распределенной вдоль оси Ох нагрузки и формы области контакта Д1я

= 80 м при перекосе в = 435 мкрад 1,5 (штриховые линии - расфт по методу независимых плоских сечений).

2.3. ПЕРЕМЕЩЕНИЯ И МИКРОПРОСКАЛЬЗЫВАНИЕ В КОНТАКТЕ

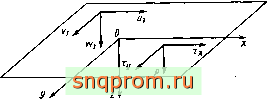
Упругие перемещения. При расчете нормальных и касательных переме-щ(ний детали подшипникового узла (шарики, ролики, кольца, сепаратор) за меняют на упругие полупространства (рис. 2.7). Ось Oz декартовой системы координат Oxyz направлена внутрь нижнего полупространства.

Пусть на детали, котактирующие по некоторой области i2 плоскости 0)iy и находящиеся под давлением р{х, у) > О, действует распределенная касательная нагрузка с компонентами Тх(х, у), Ту(х, у) для нижнего тела и ~Тх(х, у), ~Ту(х, у) для верхнего. Тогда для составляющих вектора перемещения точки полупространства имеем

1 + v:

иАх,у, Z) =--Lff-

(x-x)\z\ а - 2vj)(x - X)

r(\z\ + г)

]р{х\у')

1 - 2v,-

(X - х') (1 - 2vj)(x - х'}

г' Г(2+ гУ

(х-х')(у-у') {l~2v)(x-х')(у-у'} ]

X dxdy;

[-------]р(:с,/) +

г' r(z+ г)

1 + f;

Vj{x,y,z) =-1 Я

+ (- 1)/ - 1 ([ - > - (1 - З./Кх - x)iy - У)

1 1 - 2v-

+ Г- +-L +

>гх(х:у')+ [

г \г\ +г (1 - 2vf ) (у - уУ

г(\2\+ гУ

]ту(х;у'))

dxdy;

(2.35)

Рис. 2.7

(x-x)izl (1 2p,.)(x x)

(Izl +

о - y)\z\

(l-2vj)(y -У)

+--- Tyipc. y)

r{\z\ + r) i y\ J )

dxdy\

где

r = y/(x~xf{y-yy + z: Из формул следует, что в телах из одного материала {Е^ = Ej , = v) при Тх = Ту = О касательные (и, v) перемещения равны, но нормальные имеют противоположные знаки. При р = О, наоборот, равны и имеют одинаковые знаки нормальные перемещения, а касательные, равные по абсолютному значению, направлены в противоположные стороны. Для решения контактных задач необходимо задавать в области контакта 12 при z = О разности

и(х, y) = Ui{х, у, 0) - Uj{х, у, 0); у{х, у) = v,{х, у, 0) - (х, у, 0); {х, y) = wi {х, у, 0) - W2(х, >>, 0)

касательных и нормальных перемещений поверхностей. Для описания упругих свойств пары тел введем величины

Е'.= -(/ = 1,2); Е'= -;

1 - f/ е; + я;

,(1 + + дУЕ,

(1 + v,)E, + (1 )£ ,

1 - 2f. (1 - ,),

(1 - ,),

7 ]

Для тел из одного материала при Е' ~ El = £2, i = il = , /t = О из (2.35) следует:

u=0[Fx/iEs)]+ 0[pFyl{Es)]+ 0[kPfiEs)]-

V = 0[vFx/iEs)] + 0[Fy/iEs)] + OlkP/iEs)], w = 0[kFx/(Es)] +

+ 0[kFy/iEs)]+ 0[P/iEs)],

где Fx, Fy, P~ силы, действующие на нижнее тело в направлениях Ох, Оу, О^; S - характерный размер области контакта i2.

(Поскольку касательные силы F, Fy имеют тот же порядок, что и fP {А- коэффициент трения), можно пренебречь влиянием Fx, Fy на w, внося щ я этом относительную погрешность порядка kf< 1. Таким образом, даже да и тел из разных материалов можно с большой точностью находить ра шределение давления в контакте, не учитывая влияния касательных сил. Hi пример, для контакта стали с бронзой или алюминием значение к равно нескольким сотым, поэтому kf ~ 0,05 0,2 = 0,01. Для тел из одного материала = О, и касательные силы совсем не влияют на значение давления в контакте. При А: = О задачу о распределении касательной нагрузки также можно решать без учета распределения давления. Однако для различных материалов такой подход приводит к существенной погрешности, приблизительно равной klf. Поэтому давление может заметно влиять на разность касательных перемещений в контакте тел из различных материалов. Будем считать, что либо тела из одного материала, либо значения величин kfnk/f пренебрежимо малы по сравнению с единицей. Тогда

и (х, у) =

г 1 - V , v(x - х'У 1 , ( , , [- + J--L. ]тх(х,у) +

dxdy;

1 \vx - х)(у - у ) У(х, У) = - Щ--Txix ,у) +

2 Р(х,у') , , У) = -Г- Я-dxdy.

(2.36)

где 1/G = 0,5(1/Gi + l/Gj); Gy = £/[2(1 + Vj)] - модуль сдвига материалов

тел; R = у/(х - xf + (у'- yf /

Связь перемещений с нагружением. Обозначим/(л;, у) = 1/ Vl - (х/а ) -- (у/Ь) , где а и b - полуоси эллипса контакта. Представим вектор [ Тх, Ту, Р] внешних нагрузок полиномом по х,у: М М-т

[Tx.Ty,p]=J{x,yyi [dmq.emq.fmqVy - (2.37)

m=0?=0

Дж. Калькер показал, что в этом случае разности перемещений внутри Ц вычисленные по (2.36), представляют собой полиномы степени М:

М м-т

[и, V, w] = S Б {йтп, Ьтп, Стп)х у . m = О п = 0

(2.38) 51

Коэффициенты Отп, Ътп, Стп в (2.38) выразим через dpg, Срп, fr,g в (2.37):

М

p+q>m+ п

р>0, q > О

Е -РЧ ];

т+ 1;п+ 1

М

га! п\

р+ q > т + п

р> Q;q > О

(2.39)

2(1 - 1-)

Lran

М

р > 0;(7 > О

Коэффициенты Е^ отличны от нуля при четных р + т,д + пи2И + + р +q -т -п> Он выражаются через эллиптические интегралы:

2т+в;25+а; =--(-2) Х

V V V e)!(2S+c.)!.l

k = 0 1=0 - (2Л+ e)! (2/+Ш)!

X /(с/. A: + a + e , / + /3 + w, e) ,

(2.40)

где

I(d, i, j, e) = ( - -- - /) j!(- cos )(- sin

d = A+ a + /3- Y-S > 0;

(2.41)

Г - гамма-функция Эйлера; s = Ъ (малая полуось); е - эксцентриситет эллипса контакта; е и w принимают значения О или 1. При d = 1, -2,... значения величин, вычисляемые по (2.40), равны нулю.

Из (2.37) и (2.38) следует, что при произвольном задании локальных относительных перемещений (т.е. функций и, v, w) распределенная нагрузка может оказаться неограниченно возрастающей вблизи границы эллипса. В контактных задачах с неизвестной областью контакта равенство значения давления или касательной нагрузки на границе нулю обеспечивается выбором этой границы. Если граница - эллипс, то полином в (2.37) должен делиться на 1 - (х/а) - {y/bf, т.е. должно быть

М М - р

[Гх. Ту Р] =

S 2 {dpd, р= О О

epqJpq]xPyf.

(2.42)

Разности перемещений при этом задаются формулой (2.38) с заменой М на М+ 2. Связь [ат , Ьщп, Стп] с [dpq, epij,fpq] дается формулами (2.39), в которых надо заменить [dpq, Cpqjpq] на [dpq, epq, fpq],e на

i -E; - C/ a суммирование прово-

дить пор + q>m+ п - 2,p>0.q>0.

Полные эллиптические интегралы первого и второго рода даются формулами (2.6), (2.7), эллиптические интегралы

f/2 siniJ; coslidii C= S - ;

0 V(l - esinif-)

/2 D= f

sin ф<1ф

0 v/l - esinif-

0 Vl - esin

связаны cKmL соотнощениями

K = 2D-eC, L = (2-e)D- eC,

5 =/) - eC= - (1 - e):]/e

D = (K-L)/e\ C=[(2-e)K~2Lye\

Приведем значения e и f для A < 2, p < 2, < 2, m < 4,

и < 4, i - 0; s = b;g = у/1 - e - отнощение длины меньшей полуоси к длине бо.ч- -i; К - см. (2.6) и (2.7Я :

f%00/2=F%00 =5/:/2; 0520/4=,0. 20,3/8.

7000 =-5Л; Е%1/2= Fl=-.s(2B-D+С)12; Е%1 = -gD/s; Е\112 = F=-sgC/2;

F010 = (Z) - 35 - O/s; £ %02/4 0,02 = .з^дз.). /гО. 10 = -g2 - Q/s; E 002/2 = fojo ,c/2;

0; 01/0 = ;?0; 01 01

I2 = F%1= sD/2; E\fl2 = F\f = s(£> + 0/2;

(2.43)

rO. 01 . ; £ 11)00/4 = F 1> 0 = sL/(8);

0; 01 2 03

= -g\2D+ C)ls\ £iOT = /

1; 00/-, pi; 00

= sD/2;

E lijOO/2 = F1-00 = sS/2; E 1= IO/2 = F 1-JO = c)/2; /г1,00= (д С)/5; 1;10/2=/г1;10=2,С'/2; FlOO=-CA; Fl,01/4=;,l,01= ,3 5/(g.). F l-,00 = -ф o/s; E 1=01/2 = F 01 = ,/2;

Vo= i = -/8; E1501/2 = F1 j,oi = .(Л- 0/2.

Решение контактных задач. Изложенный метод позволяет найти распределение давления в контакте двух упругих тел по эллиптической об.-, ласти с фиксированными полуосями (например, если одно из тел является жестким, плоским эллиптическим в плане штампом или если поверхности тел содержат плоские участки, соприкасающиеся по эллипсу, а тела при этом все же с некоторой погрешностью можно считать полупространствами). Приведенное ниже решение, используют для приблизительной оценки распределения давления в контакте торца ролика- с бортиком кольца (рис. 2.8). Область контакта ABC имеет форму луночки, которую можно аппроксимировать эллипсом. Основная погрешность вносится при этом значительным отличием формы тел от полупространства.

Итак, пусть тела сжаты силой Р, приложенной в точке с координатами Хо, у о- Разность w нормальных перемещений задана формулой

w = Coo + С10Х+ С01У,

(2.44)

где Соо - сближение тел в центре; Сю hcqi - углы перекосов в плоскостях Oxz и Oyz. Постоянные Соо, Сю, Cqi определяем из условия уравновешивания внешней нагрузки силой и моментами, возникающими в контакте. Считаем, что трение отсутствует. Распределение давления

Р= С(/оо +/,o + /oi7) 11 - (х/д ) - (у/Ь)]- (2.45)

Рис. 2.8

Условия равновесия имеют вид

P = SSpdxdy = 27rabGfoo:

Рхо = Я xpdxdy = -TiabGfio \ п

РУо= и ypdxdy = -J itab Gfoi n

To, что тела контактируют по эллипсу, равносильно неотрицательности давления, т.е.

/оо + fiox + /01J =

2-nabG

Зхх- 3vv-(1+-- + -111-)>0.

Отсюда следует условие

(а/3) (6/3)

означающее, что точка с координатами Хо.Д'о должна лежать внутри эллипса, концентричного и подобного i2, так же ориентированного, но длина осей которого в 3 раза меньше. Сближение и углы перекосов определяем по формулам (2.39), (2.43) :

,л/гО;00 (1 - , Соо - 2(1 - !)£ 00 оо---- л.,

(2.46)

л. in 3(1 - v)Px

c =2{lv)E\l%o - -~-В;

. 3(1 - v)Py

Coi=2(l-i)E-Qfoi = -D.

i,bG

Согласно (2.45), давление обращается в бесконечность на границе области контакта. Это означает, что в узкой полоске вблизи границы напряжения в материале превышают предел текучести, вследствие чего теория упругости становится неприменимой. Для приближенной оценки фактического давления р* следует принять р* = min(p, НВ), где НВ - твердость материала.

Формулы (2.39) позволяют решать задачи о распределении касательной нагрузки в эллиптическом контакте двух тел под действием внешних

касательных сил Fx, Fy и момента Mz. Несущественно, является ли область контакта эллипсом фиксированных размеров, определяемых формой контактирующих тел, или же ее размеры зависят от нагрузки в силу решения Герца. Предполагаем, что проскальзывание в контакте отсутствует. Разности касательных перемещений

и = Ьх -(3/ = аоо + ooi.v; V =6 + )3x = boo + by,

где [Ьх, Ьу\ - касательные смещения; 3 - угол поворота верхнего тела относительно нижнего.

Распределение касательной нагрузки имеет вид

тх = G(doo + doijyVl -ixlaf -(у/ЬУ/ Ту = G(eoo + eioxWl-(x/af -(y/bf, поэтому

Fx = 2-nabGdoo, Fy = 1-nabGe;

Mz = IlixTy-yTx)dxdy = -nabGiado -bdoi). a

По формулам (2.39), (2.43)

5;, =aoo = 2(£°5° - vE 0° )doo= 2(K - vD)ad;

by = feoo = {E - vE 5°°)eoo = 2{K - vB)aeoo;

6,о=М2(010- 110)е,о- 2.£l04,= = 2(5 - vgQacio - 2paCdoi;

01 = - = 2(f ,Ef)d -2vE-l%o =

= 2{D- vQadoi - 2vagCeio-

Отсюда следует связь с doi. ас учетом выражений для Fy, Mz получаем зависимости

К - vD К - vB

Ьх = --- Fx; by - -Fl

nbG HBD - vLC)

(2.47)

no которым можно определять упругие касательные смещения и поворот шарика или профилированного ролика, например, при оценке момента

начала вращения вала в подшипнике качения. Касательная нагрузка обращается в бесконечность на границе эллипса. Это означает, что в достаточно узкой полоске вблизи границы эллипса касательное напряжение превышает предельное кулоновское напряжение трения fp и при этом возникает относительное проскальзывание поверхностей.

В описанных выше задачах напряжения (нормальное и касательное) имели особенность на границе области контакта. Если границы области контакта неизвестны, то они в процессе контактирования формируются так, чтобы напряжения на границе обратились в нуль. Примером такой ситуации является задача Герца. Пусть после распределения давления согласно этой задаче к одному из тел приложена касательная сила [Fx, Fy] и требуется найти касательное смещение [8х, 8у] верхнего тела относительно нижнего. Предположим, что в конатакте может возникать проскальзывание, причемF= [Fx,Fy]\ </Р. *

Область контакта состоит из области сцепления л. в которой нет относительного движения частиц поверхности, и области проскальзывания Щ, в которой касательная нагрузка достигает напряжения кулоновского трения: [тх, Ту]\ = fp. В области задаем м = бд; и v = Sj а в Щ, помимо условия \ [Тх, Ту]\ = fp, требуется, чтобы локальное проскальзывание происходило в направлении локальной касательной нагрузки [х. у]- Приведенное ниже решение удовлетворяет этому последнему условию приближенно, так как считаем, что нагрузка [тх, Ту] направлена так же, как [Fx, Fy], г не в сторону локального проскальзывания. Для построения поля распределенной касательной нагрузки из значения [гх,т^], соответствующего полному скольжению, вычитаем значение [тх. Ту], отличное от нуля только в области i2/i и пропорциональное [т^, Ту]. Область сцепления при этом является эллипсом с полуосями а , Ь , концентричным и подобным эллипсу контакта и так же ориентированным. Пусть [и', v] и [и , v ] - разности перемещений тел, соответствующие нагрузкам [т^, rj,] и [ т^, Ту]. Тогда в области П

[г',=fp = ,у ]7Г:-;1:фГ

г г а D

а вне вектор [т^ , г^. ] = 0. В области

ff tt-i

а вне Пл вектор [тх ,Ту] = 0. Здесь [тх, ] - [т^ ,Ту] = [тх , Ту]. Для разностей перемещений верны равенства: в области fi

[ , v] = [aoo,oo]+ [а2о,йго]х^+ [Дц, + [ао2,02]/S

[и , v ] = Ко .6о о ] + Ко, bi,+ [а п,Ьп]ху + К, Ь^2]у';

в области [и,у] = [и'-и ,у'-у ] = [8х,8у] . Согласно (2.39) и (2.42),

Доо-А^ 20 20 * а ,=(000-.100)Ух;

02=(F°5f-i-FHf); Yx=ffMF;

)/й*0;00 F l;00 4v -Доо -2(F 5q -i-F )Гх,

=(ГО;оо ,. i00)j.;. b;\=-2.F i:00yi;

=(/r 0:00 ,, l;00)y,. Yffpii.. ftoo=2(F0;00 ,l;0O)j..

*-=(°io°°-.Fi=oO)y. an=-2.Fl;00y ,;

=(F0;00 ,Fl)Yy; YyffooFy/F; *oo = 2(F 000 ,, l;00)y,.

=( ir- 4o°°)J7;

fl,;=-2 F l:00r;; *<=(F 0>00 , l;00)y .

=ffooFy/F.

Здесь коэффициенты F взяты для малой полуоси эллипса контакта, а F Р*? - для малой полуоси эллиптической области сцепления. Из (2.40) и (2.42) следует, что коэффициенты Ff и F Р при х^, ху и у^ отличаются только множителями 1/д и 1/д , так как в 58

(2.40) d = - I. Для равенства нулю членов второго порядка по л; и в области nfi, как того требует граничное условие, положим/оо = д /оо/д-Теперь выразим а через д с помощью формул для сил F aFyi

Fx = Я dxdj - ; Tidxdy = т^ф' - т^хф =

= [l-( - f]fPFx/F;

Fy = [l-if]fPFy/F

При этом b /b = д7д = (1 - FI(fP)y, F = V? + F]i . Что касается членов нулевого порядка в перемещениях, то из равенства d = О в (2.40) следует F = Fa /а, так что

/о о в -2/3

Доо - Доо--дооМ ~ -) ;

йoo=&oo(l-F F)

Согласно формулам (2.43), F gO = a/i:/2, F = д£)/2, F * = 5/2. Для 5х и 8у верны формулы

Sx = [l-(l- - r ]{K-uD)-

InbGF

fP 2nbGF

(2.48)

При F О получаем тот же результат, что и при расчете по формуле (2.47). При F = fP формулы (2.48) дают

2nbGF

; max r>s 3/PF,

(2.49)

2itbGF

где S, SjT** - максимальное предварительное смещение под действием силы [Fx,Fy], равной по абсолютному значению .

При дальнейшем увеличении силы начинается скольжение. При v Ф О направление локального проскальзывания не совпадает с направлением силы [Fx, Fy]. Пусть, например, Fy = О, а Fx возрастает от нуля до fP . Напряжения трения, по предположению, в каждой точке параллельны

оси Ox, то же относится и к проскальзыванию, определяемому вектором [Щх - u)ldt, д(5у - v)/dt], >-компонента которого должна обращаться в нуль. Поскольку при Fy = О смещение 5 = О, то д\1 bt = О в любой момент времени. Это значит, что в конечном состоянии полного скольжения v = О, д = О, v = О и v = v = Ьцху, где Ьц Ф О при рф. Таким образом, разность перемещений [ и, v] не везде коллинеарна [Тх, Ту\ - [гх. 0]- Для круговой области контакта наибольший угол между [ы, v] и [тх, 0] равен 9,6° при v = 0,5 и 4,1° при v = 0,25. Это позволяет считать угол между [и, v] и [г^, ту] малым. Формулы (2.48) и (2.49) используют для расчета предварительного упругого смещения в контактах подшипниковых узлов при определении моментов сил, необходимых для начала движения.

2.4. НАПРЯЖЕННОЕ СОСТОЯНИЕ в ОБЛАСТИ КОНТАКТА

Общие формулы для напряжений под эллиптическим контактом при нормальном нагружении. Напряжение в упругом полупространстве, нагруженном распределенным по области П давлением р(х, у), определяются формулами

+ 21-

Эу Э'н-

---(1-2 .)-];

, Э'у Эу 3w

[-Z - + 2р--(1-2 ;)-];

Э'у

Э'у дхЪу

Э'у

+ (1 - 2р)

(2.50)

2я ЭхЭг Z Э'у

dybz

где

v(x,>..z)=;;

а

М.Х, У. г) = Я Р(, тг)/и(г + z)dm, а

r=s/a-xy + (v-yf-z\

(2.51)

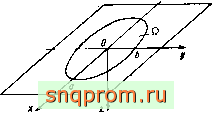
Начало О системы координат Oxyz и оси Ох, Оу лежат на поверхности, ось Oz направлена вглубь по нормали к поверхности (рис. 2.9). Если область J2 - эллипс, как на рисунке, а давление распределено согласно Герцу:

Рис 2.9

1 2 [ 3 ] 4 5 6 ... 14