Главная страница сайта  Российские промышленные издания (узловые агрегаты) 

1 ... 7 8 9 [ 10 ] 11 12 13 14

+ Р'[(-1) а*.;,Г. ,Г2 ]

(3.183)

где

P(a*.,7i,72)=Pi+ s [(cosa*-l)pm(¥-rm)+ (-1) х m= 1,2

X cosa*p2 + m(-rm) - (-l) sma*p; + ((> -Tm)] Слагаеллые третьего порядка малости из (3.183) определяются выражением

Пз= 2 s/(-l) (xcosa* + (-l) 3)cos +

86* n=l,2 /=l\ I-

+ [:cosa* - (-l) /a] sin; - (-l) zsina*j +Py, (3.184)

где - нагрузка в контакте в состоянии предварительного натяга.

Определим слагаемые, квадратичные по отклонениям геометрических параметров и линейные по координатам:

Пз, = - (-1) Б 1 [(xcosa* + i-l) m cos; +

86* =1,2 /=1

+ Cvcosa* - (-!) / ) sm,>; - (-l) zsma*] (/ У.

При учете этих слагаемых в правой части системы (3.167) появится слагаемое

ЗР* -

П= 1,2/=1

- cosa:*cosi/y

- cosQ!*sini (-l) sma*

(-l) /sin -(-l) /cosi/f

(3.185)

Определим его спектральный состав.

Воспользуемся комплексной формой (3.1) разложения отклонений геометрических параметров колец в ряд Фурье и введем комплексные амплитуды

= (cosa*- 1)ск т + (-l) cosa*c,V., )- (-1) х X sma*c;t(4 + т)

Обозначим Um ~ <с -т- Тогда 182

(Рп) = <\ sf ехр I / (2sc07*/ + а/ )

Б Б Q exp m= 1, 2 к = -оо

= Б Б dPj dj ехр j / [2 (. -h Л) со,*Г + а у- -h ajj ]

i= -оо Л= -оо I

-Ь2Б Б Б djQmexp /[(2sco7*+Лсо^)/-ь т= 1, 2 Л= -оо j= о

+ Л^о2 + а?/ + л^ (/- 1)][ + 2 Б Б Q, , X X ехр /[(Лсо! -I- SC02) f + (Л s) V00 +(* + ) О' - 1) ]

+ Б Б Б СА:;;,С, Гехр \ i(ks)X m=i,2fc=-0° s= -00

27Г

(3.186)

В зтой формуле слагаемые (колебания) обусловлены взаимодействием различных деталей подшипника с отклонениями геометрических параметров: первое слагаемое - взаимодействием шариков с указанными отклонениями; второе - взаимодействием шарика и колец; третье - взаимодействием наружного и BHjrrpeHHero колец; четвертое - взаимодействием одноименных колец с отклонениями геометрических параметров.

Определим дополнительный спектр радиальных и угловых колебаний, обусловленный первой, второй, четвертой и пятой строками выраженга (3.185). Если воспользоваться формулами Эйлера (3.172), то слагаемые первых двух групп в (3.186) приводят к появлению частот вида

2(5 + Л)С07* ± со*; 2SCJ7* + ки>гп ± с-

. п

Умножение на cosi/ , sini/: , эквивалентное умножению на е*/ - = ехр ±/ j [со*/ + ( оо + -(/ - 1) ] , приведет к появлению в третьем и

четвертом слагаемых в (3.186) сомножителя ехр j(s+ Л +1 ) 27г(/ - l)/zj. Но поскольку в (3.185) ведем суммирование по /, то ненулевыми будут лишь те слагаемые, для которьсс s + Л ± 1 = rZ. Поэтому третье слагаемое в (3.186) дает спектр вида fcco, + scoj ± со* ,гдеs± l=rZ,r - целое

число, при этом либо Wi, либо W2 равно со*. Пусть для определенности (выводы от этого не изменятся) coi = со* , coj = со* - fi. Тогда

A:coi +SC02 ± со*= (rZ + 1 -s)coi +SCO2 ± coJ=/Zco*+s(co2 -coj) = = rZojJ-sfi.

Четвертое слагаемое в (3.186) имеет спектр, состоящий из частот вида

(к + s) СОт ± = (rZ + 1) com ± со*= rZcom + (oJm - , или, в более полной записи,

rZ(co*-fi) ± fi, т = т.

Таблица 3.4

{k + s)<m ± =

Найдем дополнительный спектр осевой вибрации, обусловленный параметрами в третьей строке выражения (3.185). Первое и второе слагаемые в (3.186) обусловливают частоты вида

2(s + fe)607*; 2soj* + k<uim.

Третье и четвертое слагаемые не равны нулю при Л + s = rZ, а их спектр состоит из частот fecoi + ХСО2, {к + s) сот - rZcom. Представив А; и s в виде

k = p + riZ; s = -p + rZ,

получим

fecOi +SCO2 =p(C0i -CO2) +/-jZcOi +/-2ZC02 =pfi+/iZco*+. + r2Z(cO*-fi).

в табл. 3.4 приведены собственные частоты вибрации в кубическом приближении, которые отличны от частот, содержащихся в табл. 3.2.

Применение изложенного выще метода разрежения осевого спектра ведет также к разрежению спектра в квадратичном по отклонениям геометрических параметров приближении.

Параметрические колебания ротора. Слагаемые, квадратичные по координатам и линейные по отклонениям геометрических параметров в выражении (3.184) для П, имеют вид

ЗР* Г

Пз2=- Б S [xcosa*+(-1) /3] cosi/; +

86 л= 1, 2 /= 1 L

Угловая частота вибрации		Взаимодействующие
	радиалыюй и угловой
2fcto* + s(u>*- 12)	2sto* + A:(cj(, - 12) ± со* 2SU!* + fccjj	Шарик - кольцо ротора Шарик - кольцо ста-
pI2 + i,ZcjJ+Sj2(toJ- n)	s2toJ - кп	Наружное кольцо - внутреннее кольцо
Примечание. A, s, p, s - целые числа.

+ [; ;cosa* - (-1) /а] sin,>; - (-l) zsma*

П

Наличие полученной составляющей потенциальной энергии приводит к появлению в уравнениях движения произведений отклонений геометрических параметров и координат. Это значит, что матрица коэффициентов системы дифференциальных уравнений движения ротора (интерпретируемая как матрица жесткости) зависит от отклонений геометрических параметров D , Т^у, которые вследствие переменности углов уГ, у зависят от времени. Это приводит к тому, что в системе при определенных условиях могут возникнуть либо параметрический резонанс, либо биения низкой частоты.

Для простоты ограничимся рассмотрением только осевых колебаний, т. е. положим X = у = а = fi = 0. Тогда справедлива формула

!1= -Jzsma* Б I/>((-!) *; Эг 46 п=1,2 /=1

ЛГЛ2 )= zsmV(5/+5,). 46

Уравнение собственных осевых колебаний при = О имеет вид ЗР* -,

46- 2Zsina

Разделим обе части этого уравнения на :

ЗР - - Г- 1 1 if

Mrz +[Kz+ ~ (Di +/)/) sina*] z= JLii li(5/ -5/).

z + h,z + со/ [ 1 + />,(0] = 0z -Dz).

2Zsina

(3.187)

Здесь введено обозначение (О = (D +D*)/(4Z8*) и учтено наличие демпфирования (слагаемое hz, определяемое экспериментально).

Общее решение линейного уравнения (3.187) складывается из частного решения неоднородного уравнения и общего решения однородного (с нулевой правой частью). Рассмотрим лишь однородное уравнение

z+hzZ + coill+Pz(.t)]z = 0

(3.188)

и определим условия, при которых его решение описывает параметричес- ! кий резонанс.

Функщш Pz(.t) задается тригонометрическим рядом, коэффивденты которого зависят ог отклонений формы и размеров колец и шариков. Спектр этой функции совпадает со спектром правой части уравнения

(3.187) и, следовательно, со спектром собственной осевой вибрации (см, ) табл. 3.2). Последний же состоит в общем случае из трех серий угловых чао- тот, кратных CJ* , - со* , 2со* . Решение уравнения (3.188) при = О, м Pzit) - /coscor (уравнения Матье) описывает параметрический резонанс при близости угловой частоты со к частотам вида 2сог/и п - натуральное число. Аналогично уравнению Матье, решение (3.188) может также описывать параметрический резонанс.

Исследуем основной параметрический резонанс (и = 1). Предположим, что в функцию (О в качестве слагаемых входят гармоники с частотами 2со2 + 2е, близкими к удвоенной собственной частоте осевых колебаний (е| < Icol). Вследствие того, что функция Pit) содержит серии кратных частот, в ней могут содержаться также гармоники с частотой со + е:

Pz it) = Yo2 cos(2coz + 2e)t + 602 sin(2coz + 2e) Г + roi cos(coz + e) f + 6oism(coz + e)r-bFo(0.-

где коэффициенты 7o 1) 7o2, 601 ,602 вычисляем из формулы (3.171) для Dz , причем Poit) - функция времени, в разложение которой не входят слагаемые с частотами coz + е, 2coz + 2е. Будем искать решение уравнения

(3.188) в виде

z = a (г)cos(coz + e)t +Ь(0sin(coz +e)t + c(t),

где a (г) ,b{t), c{t) - медленно меняющиеся функции времени.

Подставим z(r) в уравнение (3.188) и пренебрежем вторыми производными по времени от функций а, Ъ, с вследствие их малости:

- 2а (coz -ь е) sin(coz -ь с) Г - в (coz + е) cos(cOz + е) Г +

ь 2b(coz -ь е) со8(сОг + е) Г - Ь(coz + е) sm(coz + е)Г +

+ hz [acos(coz + е) Г - д (со + е) sin(coz + е) Г + bsin(coz + е) Г +

+ b(coz -He)cos(coz+е)г + с] + coi* [1+ro2cos(2c0z+2е)Г+

-H5o2sin(2coz + 2e)r +7oicos(coz + е)г +5oism(coz -н e)t -н

+ o(0] [acos(coz+e)f+bsm(cOz+e)r+c] =0.

Пренебрежем вследствие малости членами порядка e/coz и после преобразований получим систему с постоянными коэффициентами, линейную относительно медленно меняющихся функций д, Ъ, с

-2согД + hzb = {oizhz - ---) д + (2соге + -)Ь -

-cozSoic;

hzo + 2coz6 = (2coze - - ) a - (cozAz + -cozjoic;

hzC=--a--0 - coz c.

(3.189)

Согласно теории систем линейных дифференциальных уравнений с постоян-ньюли коэффициентами, решение (3.189) представим й виде линейной комбинации экспоненциальных, функций от произведения времени на характеристические числа матрицы, соответствующей данной системе. Характеристические числа связаны с амплитудами отклонений геометрических параметров посредством 702, §02, 7oi, 601, коэффициента демпфирования и е - разности возмущающей и собственной частот. Предположим, что hz =0. Тогда последнее уравнение (3. 189) становится алгебраическим. Выразив из него с и подставив в первые два уравнения, получим систему двух дифференциальных уравнений относительно а и Ь. Его характеристические числа

Х=±

0 +~Уо1

(Г01 + 8о\) +

+ - (5о1 Го2 - 2701601602-Го1 Г02) i

(3.190)

Если выражение в фигурных скобках положительно, то одно из чисел X также положительно, и, следовательно, амплитуды а, Ъ являются экспоненциальными функциями. Это, в частности, достигается при больших значениях коэффициентов 5о2 и 702, непосредственно связанных с амплитудами гармоник отклонений геометрических параметров, которые порождают частоту, близкую к 2coz, и при точной настройке на резонанс (т. е. при e/coz 1). Когда подкоренное выражение отрицательно, характеристические числа чисто мнимые, что соответствует медленному гармоническому

изменению амплитуда иЬсчастотами Х|, т. е. биениям в осевых колебаниях. Наличие демпфирования, которым мы пренебрегли при получении формулы (3.190), помогает избежать резонанса системы.

3.7. динамика сепараторов в комплекте с шариками

Низкочастотные осевые биения, связанные с переменностью углов контакта. При экспериментальном исследовании осевой вибрации маховиков гидродвигателей на радиально-упорных шариковых подшипниках можно заметить биения с частотой около 1 Гц, При этом все характеристики подшипникового узла (собственная частота осевых колебаний, амплитуда вибрации на данной частоте, мощность, расходуемая при вращении маховика, положение центра масс маховика) претерпевают медленные изменения колебательного, иногда нерегулярного характера. На некотором промежутке времени биения могут и отсутствовать. Тогда говорят о режиме самосинхронизации, но он наблюдается довольно редко. В этом подразделе изложена расчетная модель осевых биений, развитая Б.В. Федосовым, и приведены формулы для вьиисления медленных изменений характеристик подшипникового узла.

Дадим качественное объяснение механизма биений. Рассмотрим только осевые колебания ротора. Пусть угол контакта для всех шариков левого подшипника одинаков и равен а', а для всех шариков правого подшипника - а^, причем подшипники одинаковы [см. формулы (3.70)], и т= 2. Вес маховика считаем малым по сравнению с усилием предварительного натяга. Вследствие упругой контактной да)ормации шарика на внутреннее кольцо и, следовательно, на вал вдоль линии контакта, соединяющей точки контакта шарика с кольцами, действует сила (по формуле Герца) Р =

3 /2

= А:о5о .гдеАо - постоянная [см. (3.7), (3.8)] ; 5о - упругое сближение. Величина 5о состоит из трех слагаемых: начального контактного сближения 5* которое создается предварительным осевым натягом; контактного сближения - (- l) zsina*, вызванного смещением Z ротора; контактных сближений 61 и §2 для левого и правого подшипников соответственно, связанных с отклонениями формы дорожек качения и шариков. Предположим, что для всех шариков левого или правого подшипников деформация вследствие взаимодействия шариков и дорожек качения с отклонениям формы и размеров одинакова. Будем считать отклонение (Рз) радиуса дорожки наружного кольца периодической функцией полярного углаi/;, отсчитываемого в плоскости наружного кольца, с периодом l-njZ, другими словами, на наружном кольце отлична от нуля только амплитуда Z-й грамоники в разложении Рз . Кроме того, будем считать, что отклонения от сферической формы шариков равны нулю. Используя выражение (3,35) для упругой деформации и разложение в ряд Фурье для Рз, получим упругое сближение в и-м подшипнике 188

б* (-l) zsina*-p3(i )cosa*= 5*-(-l) zsina*-

-cosa*(.,3e +сгзе 0

(черта означает комплексное сопряжение). Пусть /j = fi + 2n{j - 1)/Z, тогда угфугое сближение равно 5*- (- 1) z sina* + 6 л, где

6 =-cosa*(c23e+C23e ). Уравнение осевых колебаний маховика имеет вид

,t ,t * 3/2 . , 3/2

Af;.z=A:oZsina*[(5*-zsina* + 52) - (5*+zsina* + 6,) ]. (3,191)

Рассматривая вибрацию в подразд. 3.6, мы предполагали, что z, 6i, 62 много меньше 5* и после линеаризации правой части (3.191).

(б*-(-l) zsina* + S ) <б° (1 + пришли к уравнению осевой вибрагщи z + co/z=/(0,

3 (-Dz sina*+.6

(3.192)

где coz - собственная частота осевых колебаний маховика; ДО - вьшуж-дающая сила, пропорциональная 51 -82.

При вращении вала шарики вместе с сепаратором вращаются вокруг оси узла с некоторыми угловыми скоростями coci и сОс2 для левого и правого подшипников соответственно, причем в первом приближении coci = = С0с2 - Следовательно, именно 5i и 52, являясь периодическими функциями времени, вызывают высокочастотную вибрацию маховика. При таком подходе полностью игнорируется нелинейность роторной системы, в частности нелинейность закона Герца, и, естественно, модель (3.192) биений не описывает.

Теория биений, излагаемая в данном подразделе, основана на двух положениях: нелинейности закона Герца, а также различии углов контакта а и а и их изменении во времени, вследствие чего различны и переменны угловые скорости coci и сосг- Опишем качественно причины низкочастотных автоколебаний роторной системы, наблюдаемых экспериментально и интерпретируемых как биения. Отклонения формы колец обусловливают смещение маховика от положения равновесия на (Si - S2)/(2sina*). При этом среднее значение Zq смещения вследствие нелинейности закона Герца не равно нулю. Следует также отметить, что значение Zq зависит от разности угловых скоростей сОс2 - Wci

Смещение среднего значения положения равновесия изменяет средние

значения углов контакта а' и , что влечет за собой изменение разности

Таким образом, либо все изменения со временем устанавливаются, тогда наступает самосинхронизация, либо процесс не устанавливается, тогда он имеет автоколебательный характер, т. е. в системе наблюдаются биения.

Перейдем к расчету параметров движения маховика. Введем переменную и по формуле

(3.193)

где/, =5,/(25*); /2=62/(26*).

Уравнение (3.191) можно записать в виде

tOz 3/2 3/2

+/2-/, = - [(1+Л+/2-и) -(I+/1+/2+ ) ]. После линеаризации в окрестности и = О

W + COz (l +

)и=/l-/2.

(3.194)

В этом уравнении, в отличие от (3.192), имеется множитель 1 + (fi +/2)/2, характеризующий переменную жесткость узла и подтверждающий нелинейность закона Герца. Заметим, что уравнение, аналогичное (3.194), но более общее, было получено при рассмотрении параметрического резонанса в подразд. 3.6.

Поскольку смещения шариков в окнах сепаратора не учитываем, угловая скорость центра шарика одинакова для всех шариков и совпадает с угловой скоростью сепаратора

СОс = Л2П/(2Л*),

(3.195)

где П - угловая скорость маховика; /?2 и R* - расстояния от оси вращения маховика до точки контакта шарика с внутренним кольцом и до центра шарика соответственно.

Значение R-i, = pt Pi (1 - cosa) зависит от угла контакта. Изменение угла контакта а в и-м подшипнике при осевом относительном смещении Z колец

Да= -zcosa*/v*,

где V* - расстояние (в состоянии предварительного натяга) между центрами кривизны сечений наружного и внутреннего колец плоскостью, проходящей через центр шарика и ось узла.

Значение Л2 = р1 + pi - cos [ (-1) а* + Да] 2* + (-1) Х Xsina P2A.0L Из этого выражения и формулы (3.195) следуют формулы для угловых скоростей со, cjc2 сепараторов левого и правого подшипников:

Wen = с

l-(-l)

р1 sin 2a*z

2v*[p +J>? (1 - cosa*)]

где со* - номинальная угловая скорость сепаратора, равная R*ni{2R*).

Орбитальное движение шариков и вращение сепараторов описываются уравнениями

где

p°6*cosa*

Кв = сОс- ,

[Pl+Pl (1 - cosa*) ]v*

Вследствие учета лишь отклонений формы дорожки наружного кольца /1 и /2 являются известными функциями углов ifii = if) - eviif)2=>P + 0. Итак, приведенное осевое смещение и маховика, полусумма Р и полуразность в углов поворота сепараторов удовлетворяют следующей системе уравнений:

м + cozMl + 0,5/, (<р-в)+ 0,5/2 (.>Р + в)]и=/(-в) -h( -н 0); =А\ (3,196)

0 =Л - Л ( - в)-I-/2 ((/>-I-0) ],

Для дальнейшего анализа используем наиболее простой вид функций /1 и/2 (черта сверху означает комплексное сопряжение) :

fn=a c +а„* ; и=1,2; д„ =-сгзС08а*/(25*).

(3.197)

Этот вид соответствует наличию только Z-й гармоники отклонений формы наружного кольца. При s = и v = Z6 система (3.196) принимает вид

+ т?Ч1 + f2 (V ) е f2 (V) е-]м= - [f, (v) е' + f,(v ) е-*] ; (3.198)

v = -e[ + ri(v)e + f,(v)e ],

где

r} = 0JzKZojt); e = Kelut; ri(v) =д2е -Д1е

Г2(У) =0,5(й2е +а,е ),

a штрихом обозначено дифференцирование по безразмерному времени х. Значение е для приборного шарикового подшипника имеет порядок 10 , поэтому при решении первого уравнения системы (3.198) v можно считать практически постоянным параметром. Решение ищем в виде

- IS , ~is

(3.199)

где Uo и 1 - медленно меняющиеся функции, причем Uo - вещественно-значная, а Ui - комплекснозначная.

Смысл зтих функций следующий: Uo определяет медленное смещение среднего значения положения равновесия, 2\Ui\ - амплитуда высокочастотных колебаний, argu, - фаза зтих колебаний. Подстановка (3.199) в первое уравнение (3.198) с учетом малости и'о , иЦ , и'и и и приравнивание постоянных составляющих и коэффициентов при дают

Ио=2Ке(Г,Г2)/т?;

1 = (Г1 -Г2т? о)/(т? - 1);

т,- 1 n

(3.200)

Формулы (3.199), (3.200) описывают вынужденные колебания. Слагаемые, обусловливающие собственные колебания (решения однородного уравнения), не приняты во внимание вследствие наличия демпфирования в подшипниковом узле, которое мы для упрощения уравнений не учитываем. Формулы (3.199), (3.200) являются приближенными, поскольку коэффициенты при старших гармониках в разложении и не учтены, хотя они не равны нулю. При параметрическом резонансе собственные колебания могут и не быть погашены демпфированием, однако в подшипниковых узлах, как правило, условия параметрического резонанса не вьшолняются. После подстановки выражений (v) и 2 (v) в формулу (3.200) для Мо приводим ее к виду

1а, I -la, I

- Й2 COS 2(v- 7)

(3.201)

где qi =77 i 0,57?(k, + 12 I) ; ?2 = t? a,a2 I; 7 = 0,5(argai - argaj).

Выражение в знаменателе (3.201) может обращаться в нуль, что соответствует резонансу (не параметрическому), мы же рассматриваем режим, при котором резонанса нет.

Подстановка выражения (3.199) во второе уравнение системы (3.198) приводит к уравнению

v=-e ho(v)+ [ i(v)+ri(v)]e +lM,(v)+f,(v)]e l(3.202)

Для приближенного решения (3.202) проведем усреднение по быстрому времени s. В результате получим сумму медленно меняющейся функции и быстрых осцилляции малой амплитуды:

v = vo (о) + ev, (о) е + eV, (а)е'\ (3.203)

где о = ех - медленное время. Подстановка (3.203) в (3.202) с учетом только членов нулевого порядка по е дает уравнение для определения vq :

(3.204)

do q - jcos 2(v - 7) и выражение для v,:

V, =-/[u, (Vo) +ri(vo)].

Итак, задача о биениях свелась к уравнению (3.204), решение которого удовлетворяет следующему алгебраическому соотношению:

i(vo - г') - 0,52sin2(vo -7) =С(а-ао),

(3.205)

гдеС= 121 - 111; Оо - константа интегрирования.

При отсутствии резонанса левая часть этого уравнения является возрастающей функцией, поэтому (3.205) однозначно решается относительно vq. На рис. 3.21 приведены характерные графики функций vq (а) (штриховая линия) и у (а) (сплошная линия), причем v отличается от vq лишь высокочастотными колебаниями малой амплитуды порядка е.

Рис. 3.21

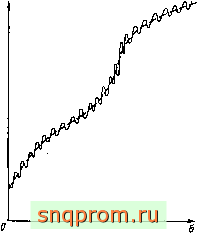
Пример 3.4. Определим основные характеристики биений. К основным характеристикам относятся период биений, среднее значение смещения центра масс маховика, изменение амплитуды огибающей высокочастотных колебаний маховика (амплитуда биений), медленное изменение собственной частоты осевых колебаний, суммарная мощность, расходуемая при работе подшипников, и разность мощностей, расходуемых при работе левого и правого подцшпников. Рассмотрим узел с подшипниками 106074 при следующих числовых данных: р° = 2 мм,= р = 1,08 мм, pJ = 5,42 мм, р° = = 3,3985 мм; 2=7; материал шариков и колец - сталь ШХ15, модуль упругости Е = = 2,1-10 Па, коэффициент Пуассона v = 0,3; угловая скорость ротора П = = 3142 рад/с; усилие предварительного осевого натягаIFI= 18 Н; масса маховика Mf - 230 г; амплитуда седьмой гармоники отклонений формы наружного кольца соответственно левого и правого подшипников такова, что 4а,6* = 0,16* и 4а,6* = = 0,26* (6* - контактное сближение в условиях предварительного натяга).

Решение. Проведем статический силовой расчет, используя метод последовательных приближений.

В первом приближении принимаем 6, = О и определяем последовательно

у = р\ +р° -Р? +6 = 1,08+ 1,08- 2,00= 0,16 мм;

а = arccos (

р.°+р +р° - Рз

) = aiccos (

3,3985 + 2,16 - 5,42

0,16

= aiccos 0,8625 = 30°40* ; 1 sinal =0,506; а < 0;

P = Fl/iZsina) = 18/(7-0,506) = 5,08 Н; Л„ =Л, = ( - -

1,08

= 13,5 мм; = ( - -

5,42 - 1,08(1 -cosa)

)- =

= (1-

0,8625

) = 1,19 мм; = (1 +

0,8625

5,42 - 1,080,14 = 0,805 мм; i?j,/i? = 0,088; Л^/Л = 0,44.

3,398 + 1,08-0,14

-)- =

По табл. 2.1 находим kg *0,79, Aj =0,68. По формулам (3.7), (3.8) вычисляем

2.110

К, =-{

0,91

= 1,09-10° Па-м

2.М0 К,= - (

13.5-10

1.19-10

0,79

0,91

= 1,13-10 Па-м Kg = 3.92-10 Па-м По формуле (3.8) 6* = (

13.5-10

/2 >

5.08

0.805 10

0.68

3.92-10

) =1,19 мкм.

Второе приб1шжение дает малую поправку значения угла контакта, поэтому ограничимся первым и примем а* = а, V* = V. Вычислим R, R *:

R* = 5,42 - 1,08(1 - 0,8625) = 5,27 мм; Л * = 3,3985 + 1,08(1 - 0.8625) =

= 3,55 мм; R* = (Л* +Л*)/2= 4.41 мм.

По формуле (3.195) определим 3.55

3142= 1264 рад/с;

2-4,41

/с=шс/(2л) = 201Гц.

По формуле (3.70) вычислим осевую жесткость: 3-5,08-7

-- (0,506) = 2,295-10 Н/м.

1.19-10 *

Собственная угловая частота осевых колебаний

Шг = sjKzlMr ч/2,295-10/0.23= 9989 рад/с; fz = zlW = 1584 Гц.

Перейдем к динамическому расчету. Определим частоту биений. Период биений -наименьший интервал времени, через который изменяется на тг. Из (3.205) получаем, что в единицах безразмерного времени а период равен п^,/ С|. Пересчет в исходное время t дает для частоты биений выражение

p 6*cosa*

г)= - 1 -0,5г]М1а, + 12 1)

(3.206)

гдеп = /г/(г/с).

Из исходных данных получаем, что а, = 0,025, = 0.05. Тогда

/б = 2-7-201

1.08-1,2-10* 0,8625 (4,48 - 1,08-0,8625) 0.16 10 0,05 - 0,025

[1584/(7-201) ] - 1 - [1584/(7-201) ] (0.05 + 0,025)/2

= 0.04 Гц.

Определим среднее значение смещения центра масс. Выражение для z (f). согласно (3.193), (3.197). (3.199), имеет вид

о* . *. ...

lijJfft - - -ICJQt

[ о + ( . +fi)e + ( !+?,) е

Отсюда среднее значение смещения центра масс

(3.207)

lz l =

sina

6* a, - la.ll sina* (?, -(?jC0s2(v - 7)

при этом минимальное значение lolmin -

максимальное значение

sina* т) - 1 - Q,5rf (la, Г - а, ) 1а,= - la.ll

sina* n - l-0,5n4a, + a,)-

Для рассматриваемого узла

1,2 0,05 - 0,025=

lomin = lolmax =

(3.208)

(3.209)

(3.210)

0,506 1,275 - 1 - 0,637 6,25-10 1.2 0,0019

= 0.164 мкм.

= 0.0162 мкм;

0.506 О, 271

На рис. 3.22 приведен характерный график зависимости и от ui%t.

Найдем амплитуды биений. Из (3.207) следует, что амплитуда А (t) огибающей высокочастотных колебаний равна 2б* , + f, /sina*. Из формулы (3.200) без отброшенных кубических по ?, и f j членов получаем

2г* rjf.i 26*4

А it) =-- - = - X

Via.! + а, - 2a,a,cos2(v - 7)

- 1 -0,5т) (а, +aj) -rjI а,а, cos2 (v - 7) При условии

п' - 1-п' (й,+а,р) -0.5п= (а. + а,) > О,

которое при указанных числовых значениях выполнено. А является убывающей функцией от cos 2 (v - 7 ). Поэтому при cos2 (v - 7) = + 1

26 *т,

a,l + aj

sina* rj - 1 - 0.5т) ((а, I - la, i) и

Рис. 3.22

lla, I - la, I

sina* n -l-0,5T)(a,l + lajl)

Для амплитуды биений, равной полуразности экстремальных значений, верна фор-

Аб- - [

а,1 - lil

sina г) - 1-0.5n4lajl - la.l) Иа,1 - ljil

т) -l-0.5T)=(a,l + iajl)

Для рассматриваемого узла

2-1,2-1,275(0.025 + 0,05)

(3.211)

0,506 (1,275 - 1 - 0,637-0.0006) 2-1.2-1.275 0.025

-= 1.98 мкм;

- = 0.67 мкм;

0,506(1.275 - 1 - 0,637-0,075) Лб = 0.66 мкм.

Определим сдвиг собственной частоты. Амплитуда колебаний z [см. формулу (3.208) ] становится бесконечной, если т)= - 1 - 2 fl т) = 0. При отсутствии отклонений геометрических параметров (f j = 0) резонанс наступает при т) = 1. т. е. при ш = = Ztog = toz; при наличии же указанных отклонений знаменатель обращается в нуль при

to = tozVl - 2l?2l = WzVl - (laH +la2l)/2- a,ajcos2(v -7).

Это можно интерпретировать как сдвиг частоты собственных колебаний, который ие постоянен, а зависит от времени через функцию Vp. Резонансная угловая частота медленно колеблется между

max = tOzVl - 0.5 (la, I - ia,l)

min = tozVl-0,5(Ia, + a,l), все Время оставаясь меньше toz- Относительное изменение частоты max - min

= Vl - 0,5 (la, I - la,l)= - Vl - 0,5 (la, I + a,)=.

Для рассматриваемого узла max - min

= ч/1 - 0.5-0,025=- чД - 0,5 0,075 = 1,25-10 0,12%.

Потери мощности в подшипниках обусловлены тремя основными причинами:

трением сепаратора о базу, сопротивлением качению шариков, угловой скоростью ш„ и дифференциальным проскальзьшанием шариков. Первые две причины приводят к тому, что в точках контакта шариков с внутренним кольцом к последнему приложена некоторая сила, тормозящая вращение маховика. В рассмотренной модели биений эта сила не учтена. Если считать указанную силу постоянной, то ее момент относительно оси вращения маховика пропорционален плечу, т. е. R*. Таким образом, это слагаемое момента сопротивления вращению

Pj sina*cosa*

(Р4 +Р2 -P2°cosa*)v

где М„ - момент (без учета динамических эффектов), обусловленный только скольжением в центрах контактов и моментами качения, действующими на шарики.

Для определения низкочастотных изменений мощности надо момент умножитьна угловую скорость маховика и усреднить по быстрому времени. Тогда мощность

Arot =М„П[1 + (-l)

p;6*cosa*

(Р4° +Р? -pJcosa*)v*

Отсюда следует, что сумма мощностей постоянна, а разность пропорциональна медленному осевому смещению центра масс маховика.

Слагаемое, связанное с u) Ф Ои дифференциальным проскальзыванием шариков, зависит от нагрузки в контактах и меняется в соответствии с медленным изменением г и фактического осевого усилия.

В изложенном методе расчета не учтены радиальные и угловые колебания маховика, а из всех отклонений формы и размеров рабочих поверхностей рассмотрена только Z-я гармоника отклонений формы желобов наружных колец. Наличие аналогичных отклонений формы внутренних колец приводит к тому, что спектр колебаний функций /, и /2 содержит много несоизмеримых частот. Более полный учет спектра отклонений приведет к обнаружению нестабильности характеристик биений типа почти периодических колебаний. В эксперименте обнаружены колебания маховика, близкие к релаксационным (разрывным). Это, вероятно, связано с попаданием колебаний подшипникового узла, возмущенного всеми видами отклонений геометрических параметров, в резонансную область.

Помимо отклонений формы, функции /1 и /2 зависят от случайных факторов, например, от распределения смазочного материала по поверхности дорожки качения, которое постоянно меняется вследствие миграции масла и срыва капель с сепаратора. Поэтому при изучении нестабильностей имеет смысл считать /1 и /2 стационарными случайными функциями с более или менее известными спектральными и корреляционными свойствами. При таком подходе можно ожидать не только почти периодических нестабильностей. Полученное числовое значение Л max сосгавляет около 70 % осевого сближения 6 /sina колец, обусловленного предварительным натягом. Отсюда следует, что линеаризация не всегда правомерна. На это указывает и возможность резонанса. В частности, шарики могут периодически разгружаться. В данной теории режиму самосинхронизации соответствует случай, когда \ai = кг I, что маловероятно.

Изложенные расчетные формулы описывают такие экспериментально наблюдавшиеся А.С. Райковым и Э.В. Строгановой эффекты, как плавание собственной частоты и среднего положения центра масс. В эксперименте замечены биения с частотами примерно 1Гц и ниже. Наблюдалась также убывающая зависимость амплитуды биений от частоты. Пусть кг I = 0,05, а kil принимает значения 0; 0,025; 0,05. Тогда по формулам (3.206) и (3.211)

/б; о =5,52

О, 05

1,275 - 1 - 0,637 0,05

= 0,051 Гц;

/б; 0,025 - 5,52

О, 05 -О, 025 0,265 - 0,637 (0,05 + 0,025)

= 0,042 Гц;

/б; 0,05 = 0; Aq; о - 0;

1,21,275

б; 0,02 5 -

0,075

О, 506 0,275 - 0,637-0,025

0,025

0,275 - 0,637-0,075

) = 0,28 мкм;

б; 0,05 =2,98

0,275

= 1,12 мкм.

Низкочастотные радиальные биения, связанные с отклонениями от сферической формы шариков. Для гиродвигателей некоторых типов частота собственных радиальных колебаний маховика отличается от частоты вынужденных колебаний, вызванных отклонениями размеров шариков, всего на несколько герц (шариковый резонанс). Ниже на простой расчетной схеме, разработанной Б.В. Федосовым, показано, что резонанс может быть одной из причин возникновения нерегулярных низкочастотных биений.

Рассмотрим маховик, вращающийся на двух радиально-упорных шариковых подшипниках, при следующих предположениях.

1. Учитываем только радиальные смещения xv.y центра масс маховика.

2. Массой шариков и сепараторов пренебрегаем.

3. Каждый подшипник рассматриваем как систему с Z -н 1 степенями свободы. Одна степень соответствует вращению комплекта шариков вместе с сепаратором. Пространственные движения центра сепаратора, а также смещения шариков в окнах сепаратора не учитываем. Таким образом, положение центров шариков задается углами + 27г(/ - 1)/Z; / = 1, ...,Z (индекс и, обозначающий номер подшипника, временно опустим). Остальные степени свободы соответствуют качению шариков и задаются углами i /. Ось вращения /-го шарика (рис. 3.23) лежит в плоскости, проходящей через

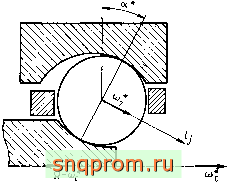
Рис. 3.23

ОСЬ подшипника и центр шарика, и перпендикулярна линии, соединяющей точки контакта с кольцами; ф/ ~ угол поворота шарика вокруг этой оси в системе координат, связанной с сепаратором.

Кроме вращения вокруг оси /у, шарик участвует во вращении вместе с сепаратором вокруг оси подшипника. Проекция вектора полной (в неподвижной системе координат) угловой скорости шарика на ось /у равна \pj - фсова*, где а* - угол контакта в условиях предварительного осевого натяга. Действительно, если при неподвижном сепараторе поверхности наружного кольца и вала движутся так, как показано на рис. 3.23, то вектор относительной угловой скорости CJ* шарика направлен по стрелке вдоль оси Ij. В то же время вектор переносной угловой скорости шарика, центр которого неподвижен относительно сепаратора, направлен на рис. 3.23 влево. Сложение двух векторов дает приведенную выше формулу, первое слагаемое в которой определяет момент сил трения, действующих на шарик.

4. Из всех отклонений размеров и формы учитываем только отклонение от сферической формы шариков. При этом отклонение среднего диаметра шарика есть функция угла ф^:

Pv ( ) = 2 u?fc/exp \Ц2кф1 + akj)

где d.j = = 0,5j7 {к Ф 0) - йоловина амплитуды к-й гармоники; dgj = Aqi - Рт - разность между средним и номинальным диаметрами шарика; aj = - а kj - постоянная фаза.

Отметим, что разложение в ряд Фурье р, содержит только четные гармоники. Суммирование по к проводится от - оо до °°, xoto на практике учитывают только несколько первых гармоник.

5. Рассматриваются только два вида сил: упругое взаимодействие шариков с кольцами по линеаризованному закону Герца и силы вязкого трения в контактах шариков с кольцами. Потенциальная энергия ротора, как следует из формулы (3.82),

П = Кг(-- + Re

(JC - ( S S Ck) X к / = 1

X ехр {2kфj + Vl) I + ехр i{2k ф} +

+ -1 2 2 S dfc ехр 1 1{2кф1 + а^;- )}. +

3Zcosa* = 2/=1 к I

+ -2 2 dkjdljX

2Zcosa ,г= 1, 2 / = 1 k,l

X ехр I / {2к ф, + 21ф + akj + а, )

(3.212)

где

cfc/ = г-- ехр

Zcosa

2 , п

Считаем, что сила и момент, действующие на шарик, линейно связаны с отклонениями cjc.cj; откинематическихзначений [см.формулы (3.163)]. Кроме того, положим в (3.163) Ai ал =/Tjsi. тогда

Fcr = (1 + 2 0Ls2)R* (с^с - wc*) = 2jfi a,yR* (w - со*); Ml = 0,51 as,P7° (со; - со*) = О.зГ, a p7° {фj - CO7*),

о

где со* - номинальное значение фj для шарика, который катится без прост кальзывания.

Силы, действующие на сепаратор со стороны каждого шарика, равны - Fg, а момент относительно оси симметрии подшипника, действующий на сепаратор,

М= - р (f- сос*); р = 2Zi 51?*

Обозначим v = 0,5Ki а^р?- Использовав выражение (3.135) для Km, получим

д =2nZR---кцаф;

=0.5я(рО)-°;> -где а Ь, - большая и малая полуоси эллипса контакта.

(3.213)

1 ... 7 8 9 [ 10 ] 11 12 13 14