Главная страница сайта
Российские промышленные издания (узловые агрегаты)
1 ...
3 4 5 [
6 ]
7 8 9 ...
48 входящих в соединение. При этом используются следующие расчетные формулы
1) на растяжение или сжатие
F>
(66)
2) на срез или скалывание
Ь
Fcv>
3) на смятие
Рем
fcM>
(67)
(68)
Входящие в расчетные формулы площади являются гоюща-дями нетто, т. е площадями, в которых учтено возможное ослабление за счет различного рода отверстий, выкружек выточек и 1. п.
Если одна и та же площадь рассчитывалась на срез и смятие, то берется большая площадь из полученных
Практически не всегда можно выдерживагь условия равной прочности элементов соединений. Обычно вступают в силу еще дополнительные конструктивные сообрагкения Они обос-новываюгся в курсах деталей машин, металлических и деревянных конструкций
Пример 14. Дано: Р = 4 Г; la] = 1600 кГ/см. 1тI ==
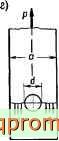
-1200 кГ/сл*; [о„,=3200 кГ/сл42 (рис 29, а).
Определить d, 8, а, Ь.
Решение 1. Определение диаметра штыря d из условии прочности на срез (рис 29, б)
2=2£=> Р., d> 1/ 2 4 - 101 1.46 см
4 Itl * Г К г. .12 10
Н
ILJL
т
Рис 29
50 -
(5,= г б,= гб,= ?
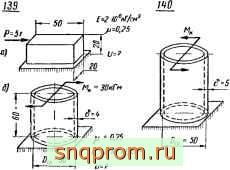
Е=г Ю'кГ/см
V. РАСЧЕТ ПРОСТЕЙШИХ СОЕДИНЕНИИ ЭЛЕМЕНТОВ КОНСТРУКЦИИ
В различных соединениях (болтовых, шпилечных, шпоночных, клиновых, заклепочных, сварных, деревянных врубках и т д ) по разным плоскостям элементы испытывают растяжение, сжатие, сдвиг и смятие
Если растяжение и сжатие обычно происходят в чистом виде, то чистый сдвиг практически не встречается Сдвигу всегда сопутствует либо изгиб, либо растяжение или сжатие, поэтому по плоскостям сдвига, кроме касательных, действуют еш,е и нормальные напряжения. Однако, поскольку величины этих нормальных напряжений малы по сравнению с касательными напряжениями, технические расчеты производятся только на сдвиг, который для металлических элементов называют срезом, а для деревянных - скалыванием Обычно считают, что по плошади среза или скалывания (Fp) касательные напряжения распределены равномерно. Допущенные неточности компенсируют величиной допускаемого касательного напряжения [т)
Смятие представляет собой местное (поверхностное) сжатие давящих друг на друга элементов Так как точный закон распределения давлений по сминаемой поверхности неизвестен, то для упрощения технических расчетов условно принимают давления распределенными равномерно не по сминаемой поверхности, а по площади (FcJ, являющейся проекцией сминаемой поверхности на плоскость, перпендикулярную направлению давящей силы Р^. Эта неточность также учитывается величиной допускаемого напряжения на смятие [а^ I.
Для рационального использования материала расчет соединений должен производиться из условия равной прочности элементов.
P=Wr
P=120kh
гу X


.J
-l-i -oKf
Р = В00ен
--г
VI. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ -ПЛОСКИХ ФИГУР
§ 1. Площади и их статические моменты
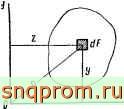
Статическими моментами площади фигуры относительно осей г и {/ ( рис 30) называются определенные интегралы вида
zdF,
Л (69)
2 Определение толщины листа 6 нз условия прочности на смятие (рис 29, в):
8d>
4.10->
1,46 - 32. Ю'
= 0.86 СМ.
3 Определение ширины полосы а из условия прочности на разрыв (рис 29, г):
(a - d)b:~; а = + d =---1-1,46 2,92сл.
* W 8[о] 0.86- 16- Ю'
4. Определение длины конца полосы из условия прочности на срез (вырез) (рис 29, д);
4 10->
2fc6>
2 . 0,86 12 10
1,94 см.
Отсюда = 6 + -у = 1,94 -I- 0,73 = 2,67 см
Задачи 141-149. Определить все размеры элшентов соединении, указанных на рисунках
Расчеты производить из условий равной прочности элементов. В задачах 146-148 принять [о] = 1600 кГ/см; [т] = 1200 кГ/см; [oej,] == 3200 В задачах 144, 145, 149 принять [о] =
= 160 Мн/м^; [т] = 120 Мн/м^; \а„] = 320 Мн/мК
777777
1 P=J,?7
[б] = ЮООнГ/см
Тогда по формуле (69)
ь
2(2л+,1) 2(2л+1)
Из выражений (70) координаты центра тяжести фигуры получают значения:
| Ь^с(п + \) (л + 2) fee | n+1 n+2 | |
| | Й + 1 | n + \ |
| 2(2 + l) | | 2(2л+ 1) |
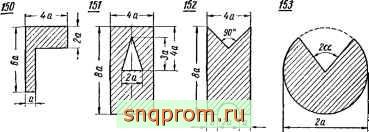
Задачи 150-155. Определить положение центра тяжести фигуо.

NfS
126-125Ю
-г4020
§ 2. Моменты инерции площади фигуры
Определенные интегралы вида
Iy=\z dF
3 Заказ N. 886
где F - площадь фигуры, dF - ее элемент, а г ау координаты этого элемента
Координаты центра тяжести фигуры Zc и {/ определяются отношениями
(70)
Статические моменты площади фигуры относительно центральных осей равны нулю.


Рис. 30
Рис 31
Пример 15. Определить координаты центра тяжести площади фигуры, ограниченной прямолинейными отрезками Ь, с п параболой у = az (рис 31)
Решение. Берем элемент площади фигуры dF = ydz = = az dz, тогда площадь фигуры
FdF ajzdz
п 4- 1
Статический момент площади F относительно оси у определяем по формуле (69)
,= zdF = a 2 + dz
п + 2
п + 2
Для определения статического момента площади фигуры относительно оси Z берем элемент площади
dF = (b - г) dy an(b - z) г - dz.
Главные моменты инерции площади фигуры, т. е. осевые моменты инерции, вычисленные относительно главных осей инерции, имеют следующие экстремальные значения:
(77)
Если /уг<0, ТО главная ось, относительно которой момент инерции максимален, проходит через I и П1 квадранты
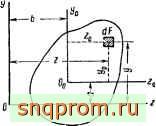

Рис 33
Рис. 34
Если /уг>0, то главная ось, относительно которой момент инерции максимален, проходит через и /V квадранты.
Главные оси, проходящие через центр тяжести площади фигуры, называются главными центральными осями, а моменты инерции относительно этих осей - главными центральными моментами инерции.
Положительные значения величии
(78)
называются радиусами инерции плоской фигуры относительно со-omeemcmeywuifiu оси.
Эллипс, построенный по уравнению
(79)
называется эллипсом инерции фигуры. Здесь оси у н г - главные оси инерции фигуры Обычно эллипс инерции строится на главных центральных осях плоской фигуры.
Ось симметрии плоской фигуры является главной осью инерции этой фигуры Любая ось, перпендикулярная оси симметрии, яв-
3* 67
называются осевыми, линейными или экваториальнымимоментсши инерции плацади фигуры (рис, 32) относительно оси г н оси у;
l =jyzdF
(72):
- центробежный момент инерции площади фигуры относительно двух взаимно перпендику1Ярных осей г к у;
l, = jpdP = I + I,
(73)
- полярный момент инерции площади фигуры относительно начала координат О.
Моменты инерции для параллельных осей, одни из которых (г^Р^о) Z. центральные (рис 33):
Рис. 32
л = /.. + (°-*)
Моменты инерции для повернутых осей (рис. 34):
(74)
г-у
COS 2а +/ sin 2а,
g sin 2а +/ cos2a,
4. =
(75)
Главные оси инерции плоской фигуры, т е две взаимно перпендикулярные оси, относительно которых центробежный момент инерции площади фигуры равен нулю, занимают положение, определяющееся уравнением
tg2a=-i. (76)
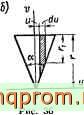
Площадь элементарной полоски толщиной dv
dF = tttdv --vdv.
Осевой момент инерции площади треугольника относительно оси и
г
ll= vdFltfldv-
Площадь эчементариой полоски толщиной du (рис. 36, б) dF = r,du-{a - 2м) du.
а
Осевой момент инерции площади треугольника относительно оси v
/;=2 f mW = 2- J u(a-2u)du==-.
Полярный момент инерции площади треугольника относительно точки О
.... аг а^г sinjWJ
+-1-=A3i cos-l.(3cos= + sin-) =
= sin a (2 + cos a).
Так как все треугольники, на которые разбивается -угольник, равны между собой и опираются вершинами в точку О, то полярный момент инерции площади всего л-угольника относительно точки О
/р = /р = sin а. (cosa + 2) = - sin а. (cos а. + 2).
В правильном -угольнике имеется не менее 2 осей симметрии, которые не перпендикулярны друг к другу, поэтому все центральные оси являются главными осями инерции и моменты инерции площади многоугольника относительно них равны между собой и равны /, отсюда
/ = -i- /р = sin о (cos а -Ь 2) = sin а (cos а + 2).
ляется второй главной осью инерции фигуры для точки их взаимного пересечения.
Если плоская фигура имеет хотя бы две оси симметрии, не перпендикулярные друг другу, то все оси, проходящие через центр тяжести этой фигуры, являются ее главными центральными осями инерции. Осевые моменты инерции площади фигуры, вычисленные относительно этих осей, равны между собой.
Пример 16. Для правильного -угольника со стороной а (рис.35) определить главные центральные моменты инерции, полярный момент инерции и построить центральный эллипс инерции.

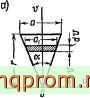
Рис. 35
Решение. Центральный угол, опирающийся на сторону а,
2к
Радиус описанной окружности
2sin-
Радиус вписанной окружности
r = cos--.
Рассмотрим одни треугольник с углом а при вершине (рис. 36, а) и найдем для него осевые моменты инерции / , 1\ и полярный момент инерции /р.
1 ...
3 4 5 [
6 ]
7 8 9 ...
48

