Главная страница сайта  Российские промышленные издания (узловые агрегаты) 

[ 1 ] 2 3 4 ... 24

ШЕСТЕРЕННЫЕ НАСОСЫ

Из шестеренных насосов наибольшее распространение получили насосы, состоящие из пары шестерен с внешним зацеплением н с одинаковым числом зубьев эвольвентного профиля.

Принцип работы шестеренного насоса рассматривается по конструктивной схеме. Приведенной на фиг. 1.

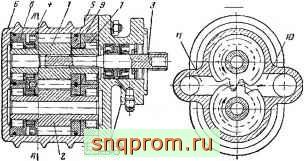
Фиг. ]. Конструктивная схема шестеренного насоса.

Прц вращении шестерен область всасывания создается там, где зубья выходят из зацепления, а область нагнетания там, где они входят в зацепление.

При указанном па фиг. 1 направлении вращения шестерен жидкость, заключенная в объемах, образованных впадинами зубьев и плотно охватывающими их расточками корпуса, переносится из полости всасывания 10 в полость нагнетания .

Ведущая шестерня 1 насоса приводится во вращение рессорой 3, связанной с ведущей шестерней и с приводом при помощи шлицевых соединений. Цапфы ведущей шестерни опираются на ролики 7 с сепаратором, расположенные в обоймах 8 к 9. Ведомая шестерня 2 свободно вращается в роликоподшипниках.

со спиральными зубь-с шевронными зубь-

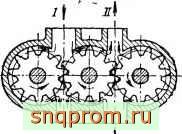
Фиг. 2. Схема

трехшестеренного

В корпусе насоса 6 выполнены полости всасывания 10 и нагнетания JJ. Расположенные с одной стороны шестерен подвижные (плавающие) подпятники- поджимаются к торцам шестерен (силой давления жидкости, подводимой с линии нагнетания, и небольшой силой пружин. Эти силы прижимают другой торец шестерни к неподвижной обойме 5. Помимо приведенного типа насоса, применяются также следующие конструктивные схемы:

а) с внутренним зацеплением;

в) ями;

г) двух- и трехвинтовые;

д) двузубые или барабанные;

е) двух- и трехступенчатые;

ж) комбинированные цен-тробежно-шестсренные и др.

В дальнейшем будет рассматриваться главным образом основной тип шестеренного насоса.

Большой практический интерес представляет иасос, выполнен 1гый по схеме трехшестеренного насоса, в котором средняя шестерня является приводной (фиг. 2); при вращении ее в направлении, указанном стрелкой, жидкость будет засасываться из каналов / и / и нагнетаться через каналы и /V. Теоретическая производительность такого насоса в два раза больше производительности насоса, состоящего из двух шестерен тех же размеров. Действительная производительность насоса этого типа из-за увеличения утечек и снижения объемного к. п. д. будет несколько ниже удвоенной производительности насоса, выполненного по обычной схеме.

В станкостроении, где шестеренные насосы широко распространены в гидропередачах сверлильно-расточных, фрезерных, токарных и шлифовальных станков, рабочее давление в них, как правило, не превыпшет 30 кГ/см и лишь в некоторых типах станков применяются насосы высокого давления до 70 кГ/см.

В настоящее время в сельскохозяйственной машиностроении и в авиации получили широкое применение насосы основного тппа с давлением нагнетания порядка 100 кГ/см и выше. Отдельные конструкции насосов удовлетворительно работают при давлении масла, свыше 300 кГ/см.

Авиационная промькиленность выпускает серийные насосы основного типа производительностью около 400 л/мин, а также опытные образцы производительностью 600 л/мин и выше Рабочей жидкостью в этих насосах является керосин.

Глава I

ТЕОРИЯ ЭВОЛЬВЕНТНОГО ЗАЦЕПЛЕНИЯ

§ 1. свойства эвольвентного профиля Эвольвентная функция угла

Эвольцентой или разверткой окружности называется плоская кривая, описываемая любой точкой прямой, перекатывающейся без скольжения по окружности.

Развертываемую окружность будем в дальнейшем называть основной окружностью. Радиус ее обозначим через Го.

Касательная к основной окружности является нормалью эвольвенты, а точка касания - ее центром кривизны. Радиус кривизны эвольвенты, как известно из способа построения этой кривой, равен длине касательной.

Рассмотрим основные положения, облегчающие определение геометрических параметров зацепления, и выведем формулы для определения элементов профиля зуба.

Введем понятие об эвольвентпой функции угла - разности между тангенсом угла а и величиной его в радианах.

Эта функция называется инволютой угла и выражается следующей зависимостью:

inva=tga-а.

Значения инволют для различных углов приведены в приложении 1.

Известно, что если из произвольной точки эвольвенты А (фиг. 3) провести радиус-вектор АО, соединяющий эту точку с центром развертываемой окружности, касательную АВ к основной (развертываемой) окружности и радиус ОВ в точку касания н обозначить угол между эгими радиусами через ф, то угол СОЛ = р между радиусом-вектором АО и радиусом, проведенным в точку С начала эвольвенты, равен инволюте угла ф, т. е. P=invi}).

Действительно, по условиям определения эвольвенты длина дуги СВ равна катету АВ, величина которого определяется из треугольника ОАВ:

Следовательно,

о

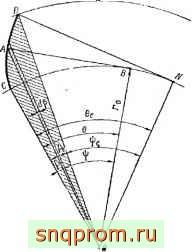
Фиг. 3. К выводу свойств эвольвенты.

Определение площадей, ограниченных эвольвентпыми кривыми

Обозначим через Sj площадь, ограниченную эвольвентой cad и двумя радиусами-векторами ос и 0d, проведенными из начальной и конечной точек эвольвенты (см. фиг. 3). Для определения площади S, выделим элементарную площадку с углом rfp. Обозначив радиус-вектор oa через q, получим

После интегрирования получим

Так как

q=rl(\+n (2)

3=invф-=С - arc tg 6

dS=-dG, 13)

1 + 62

TO, используй значения и dp из уравнений (3) и (2), получим

I 2 J l+B2 2 J

о о

Докажем, что формулу (4) можно применять также для определения площади Si, ограниченной эвольвентой CAD, касательной, проведенной из конечной точки D эвольвенты к основной окружности, и дугой этой окружности между начальной точкой эвольвенты С и точкой касания Л (1-е свойство эвольвенты):

Определенную выше площадь Si (см. фиг. 3) можно получить как разность двух площадей: S2 = Socadno, т. е. площади, ограниченной эвольвентой, двумя радиусами ОС и ON и касательной DN, и площади S3=SoD.v-

Искомая площадь S4=Scadnbc также является разностью между площадью Sj и площадью сектора 5б=5осв .

Следовательно:

Так как

S л-So-Sr,.

S=~-ON-ND.

К

Площадь сектора SsSs равна той же величине поэтол1у

Эта формула щироко используется как при определении теоретической производительности насоса, так и при подсчете геометрических параметров шестерен.

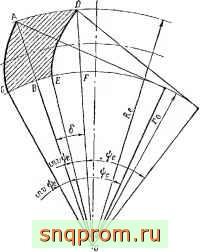
Фиг. 4. К определению площадей, ограничен ных ЭБОЛьсептпымн кривыми.

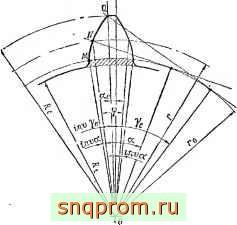
При выводе формулы для определения теоретической производительности шестеренного насоса используется еще одна формула, определяющая площадь, ограниченную двумя эвольвентами СА и ED, дугой основной окружности, описанной радиусом основной окружности / между началом этих эвольвент н дугой окружности, описанной радиусом окружности Rc головок (см. заштрихованную площадь на фиг. 4).

Обозначим эту площадь через Sj и докажем, что она равна площади So, ограничен1юй той же дугой AD, проведенными из точек А и D радиусами и отсекаемой ими на основной окружности дугой BF, т. е. части площади сектора ОАО, заключенной между

основной и внешней окружностями (2-е свойство эвольвенты). Кроме того, обозначим

Sio - DEF-

Тогда

S,=S,-\-S,;

б 2 ~

5r-Si, - -

Следовательно:

Определение площадей зуба и впадивы

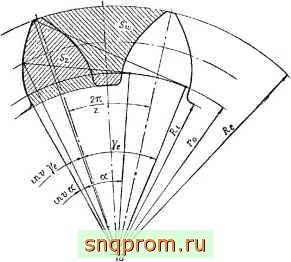
Согласно формуле (1) угол между радиусом-вектором ON (фиг. 5), проведенным в точку N эвольвенты, расположенную на

Фиг. 5. К определению площади зуба.

начальной окружности, и радиусом ОМ, проведенным в начальную точку М эвольвенты, равен inv о, где о - угол зацепления

передачи (угол давления зуба), а угол между радиусом-вектором OQ, проведенным в конечную точку эвольвенты Q, и радиусом начальной точки ОМ равен invye- Угол ус определяется из равенства

Ye=arccos -, (6а)

где Го - раднус основной окружности; Re - раднус окружности головок.

Центральный уго.п ф, соответствующий дуге зуба по нача.пьной окружности, равен я/z при беззазорном зацеплении.

В действительности между зубьями имеется боковой зазор, величина которого по дуге начальной окружности равна As. Следовательно:

JC As

П.пощадь зуба Sj можно получить, если к сумме двух равных площадей, ограниченных дугами, описанными радиусами Re и / и самими эвольвентами, прибавить площадь кругового сектора с центральным углом ае и радиусом Re и вычесть площадь кругового сектора с центральным углом ф-f 2 inv а, ограниченного радиусом Го.

Согласно формуле (4) площадь, ограниченная радиусами-векторами из начала и конца эвольвенты и самой эвольвентой, равна

Следовательно, искомую площадь зуба можно определить по следующей формуле:

2r(Y-hinvY Rlae >-g(y-f2 1nv g)

6 ~T~ 2

Подставляя значения угла с1с=ф-Ь21пуо-2invYe в приведенную выше формулу, получим

После преобразования получим

/?(-fir,va-invv.)-r (f+inva).

- (--+tav о )] + (A + inv a - inv V, ). (7>

По формуле (7) можно определить величину площади рабочей части зуба, ограниченной вольвентным профилем и основной окружностью.

Полную площадь зуба S можно опреде.пнть, прибавляя к найденной площади Si дополнительную площадь AS, (заштрихован-

площадь на фиг. 5) между основной окружностью и окружностью впадин (без учета закруглений)

где

Фи1 6. К определению площади впадины Тогда полная площадь зуба определяется по формуле

Slrl fe+J )+ -I- inv a- inv V, ) -

-/?f(-i + tava).

Площадь впадины S можно определить, если из площади S , ограниченной двумя эквидистантными профилями соседних зубьев, вычесть площадь зуба (фиг. 6).

Но согласно формуле (6)

Таким образом:

-/?(- + inva-mvv,)-r [ildlip После преобразования получим

S =/?=[--(-- + mva)+invY,

Аналогично площади зуба полная площадь впадины, включая вредное пространство, т. е. пространство до окружности впадин, определится из равенства

- ;?(--+ lnva-inv у, )+/?(--+lnva ) + (г^ /?) ; Rl[~-+inv V. - inv а ) -

Определение некоторых размеров эвольвентного профиля

(10)

Толщину зуба S:c по окружности радиусом можно определить, если будет известна толщина зуба s по окружности радиусом г и угол давления а (фиг. 7).

Угол, опирающийся на дугу радиуса г^:

-1-2 inv о - 2 inv Uj.. Толщина зуба Sx по дуге радиуса равна Sjc=r9.=r{-y+2 inv а- 2 inv а^).

(12)

Расстояние Г[ от оси шестерни до оси ролика радиуса Гр, помещенного во впадину зуба, можно определить, если известна толщина зуба по какой-нибудь окружности.

Например, если известна толшина s по зубомеру, то угол, опирающийся на дугу радиуса г, будет равен

tp=2arcsln

2г

(12а)

[ 1 ] 2 3 4 ... 24