Главная страница сайта  Российские промышленные издания (узловые агрегаты) 

1 ... 3 4 5 [ 6 ] 7 8 9 ... 18

тельное напряжение на наружной поверхности зубчатого колеса при у = б,(,) и г = определяется уравнением

Полагая, что = -f > уравнение касательного напряжения получит вид

Сила трения, действующая на участке наружной поверхности ротора, охватывающей один зуб и одну междузубовую впадину определяется следующим уравнением:

Тогда момент трения Мщ ж (рр в периферийном зазоре, возникающий при движении рассматриваемого участка ротора, определится по формуле

Суммируя моменты трения для уплотнительиой зоны обоих роторов, получим уравнение для результативного момента:

т ж (р)

После некоторого преобразования формула приобретает следующий вид:

-bru)P, + u>R,-

j=i 1=1

(75)

где - число зубьев в уплотнительиой зоне одной шестерни.

Вычисление момента периферийного трения на участках нагнетания и всасывания ж (р к) можно сделать по следующей приближенной формуле, полученной в результате решения уравнения движения жидкости (уравнение Эйлера)-

Mm. ж ,р. К) = 6,7(х (Р„, ± р ) Rib, (76)

где - угол камеры нагнетания, а р^ - угол камеры всасывания.

Как показывают расчеты, значения момента периферийного трения на участках рабочих камер насоса {Mm ж{р к)) во много раз меньше (примерно в 100 раз) значений Mm ж (т) и (М^ м;(р))-Это позволяет пренебречь его величиной.

Расчетные формулы для СостайляЮЩИХ

т.м = т.з + Mm п (1) И М„ = Af . у„ + п(2)

приведены в последующих разделах книги при расчете элементов конструкции насоса.

3. ПОТЕРИ НА ВСАСЫВАНИИ

Потери на всасывании связаны с разрежением во всасывающей камере насоса, при наступлении которого происходит неполное заполнение междузубовых впадин и возникает кавитация.

Недозаполнение возникает в результате недостаточной скорости \ поступления жидкости. Скорость прохождения жидкости через щель, образуемую расходящимися боковыми поверхностями зубьев, определяется разностью давлений в камере всасывания и в наиболее удаленной точке междузубового пространства. Понижение абсолютного давления во всасывающей камере до некоторого его критического значения способствует выделению из жидкости паров, легко кипящих фракций жидкости и воздуха, которыми заполняется часть объема камер.

Производительность насоса в условиях кавитации определяется не только напором, числом оборотов и вязкостью жидкости, но и величиной минимального давления в зоне всасывания, скоростью движения жидкости на рабочих органах, количеством присутствующих в нагнетаемой жидкости паров и воздуха и упругостной характеристикой жидкости.

Кавитация может носить местный характер, когда образующиеся при определенной величине абсолютного давления кавитационные зоны уничтожаются в период прохождения междузубового пространства через камеру всасывания, или быть более значительной, когда скорость вращения роторов и давление в зоне всасывания таковы, что кавитационные пузыри в вышедших из зацепления пространствах не успевают уничтожаться в период нахождения этих пространств в области всасывания.

Нельзя поэтому связывать потери в зоне всасывания лишь с величиной абсолютного давления на входе в насос. Более того, насос может иметь неудовлетворительные всасывающие свойства даже при нормальной величине разрежения на входе.

Основными составляющими внутренних потерь на всасывании являются:

1) Лр, - потери, обусловленные центробежной силой, препятствующей заполнени1р жидкостью рабочих камер;

2) Лрг - потери на жидкостное трение во всасывающей камере;

3) Лрз - потери на удар, вызываемый внезапным расширением пространства при переходе (на коротком участке) жидкости из трубы круглого сечения в камеру прямоугольного сечения большей площади нежели площадь всасывающей трубы;

4) Лр4 - потери на входе в междузубовое пространство и при движении по междузубовой щели;

62 < i

5) АРб - Потери на ускорение жидкости при переходе от скорости во всасывающем трубопроводе (канале) к скорости на периферии роторов;

6) Лрв - инерционные потери, обусловленные переменным (по времени) значением скорости подачи.

2-

				л
			у
		г

3

15 50 75 100 П5 150 175 тртст Потери на ВсасыВании

Фиг. 30.

Нормальная (бескавитационная) следующей зависимостью:

работа насоса определяется

- 2Ар, <р<.

где Др р - потери во всасывающем трубопроводе; р, - давление парообразования нагнетаемой жидкости; Я^ - статическая высота всасывания.

Если обозначить р^ = Ра - У^ст - Ар р, то условие бес-кавитационной работы примет следующий вид:

, : Psc-Pt<JPr .

Левая часть этой зависимости представляет собой абсолютное давление на входе во всасывающую камеру насоса.

На фиг. 30 изображена в виде кривых полученная экспериментальным путем зависимость между абсолютным давлением во всасывающей камере, основными составляющими потерь напора и производительностью насоса [19]. Экспериментально удалось выяснить лишь три составляющих, потери, обусловленные действием центробежных сил (Дрх), потери на входе в междузубовое пространство (ApJ и потери на входе в насос (Дрз). На графике видно, что с изменением абсолютного давления на входе изменяется и центробежная сила (кривая ]). Объясняется это тем, что с понижением давления междузубовые впадины частично заполняются выделившимися из жидкости парами и воздухом, в результате чего уменьшается величина центробежной силы. До точки а, принадлежащей одновременно кривым 2 и 3 я, соответствующей, примерно, 75% производительности насоса, эти кривые совпадают. В точке а начинают

Ёозййкать потери, связанные с проталкибанйем жидкости МежДу вершиной одного зуба и боковой стороной другого в увеличивающееся пространство, ограниченное этими зубьями ( потери в зубцах ).

Эти потери зависят от положения зубьев и изменяются в процессе поворота роторов. В первые мгновения после выхода контактирую-щихся зубьев из зацепления они имеют наибольшую величину, а затем постепенно уменьшаются и исчезают совсем. Например, для роторов с семью зубьями потери на вход в междузубовое пространство становятся равными нулю при повороте на 45° с момента выхода из зацепления пары зубьев, образующих междузубовое пространство.

Отдельные составляющие внутренних потерь на всасывании могут быть определены с помощью следующих расчетных зависимостей I

(О

Не будет большой погрешности в расчетах, если пренебречь составляющей потерь Др?, представляющей потери на трение о стенки камеры всасывания. Это допущение оправдывается потому, что потери на трение во всасывающей камере незначительны и частично компенсируются в предположении, что весь скоростной напор во всасывающем канале корпуса насоса расходуется на удар.

Ap-y±:AcyA=(Q\jL (77)

Арз У 2g 2g [al } 2е

где 1 - скорость жидкости во всасывающей трубе насоса, 2 - скорость жидкости во всасывающей камере насоса; dg - диаметр всасывающей трубы. Потери при заполнении междузубового пространства складываются из потерь на удар при входе в междузубовое пространство и потерь на трение при движении жидкости в нем и определяются из уравнения:

Где X - коэффициент сопротивления эквивалентного круглого трубопровода,

- среднеприведенная скорость движения жидкости в междузубовой щели, 1щ - среднеприведенная длина междузубовой щели; г^р - гидравлический радиус сечения междузубовой щели. При определении значений коэффициента X необходимо учитывать характер движения жидкости в пространстве между профилями зубьев

Исследования показывают [31], что характер движения жидкости в узкой щели находится в переходной зоне от ламинарного к турбулентному при значениях критерия Рейнольдса Re > 150:

Поэтому величина потерь должна определяться как для ламинар.

ного {к = 96 Re), так и для турбулентного {К = 0,3164 j/ Re)* потока. Коэффициент Рейнольдса для некруглых сечений определяется из известного соотношения

Для узкой щели с размером, представляющим среднеприведен-ное расстояние между боковыми поверхностями зубьев и шириной, соответствующей ширине роторов Ь, величина гидравлического радиуса, равного отношению площади живого сечения потока к смоченному периметру, находится из следующего уравнения.

-гр =

2(Ь + Сщ)

Если в знаменателе пренебречь слагаемым С^, очень малым в сравнении с b (С^ С Ь), это уравнение примет вид:

Р ~ 2Ь ~ 2

Тогда

62V60

После подстановки найденных значений Re, X, и^ и г^р в уравнение для определения АР4, оно приобретает следующий вид

АР4 =

( ОгП

2Л1щ 6062V \

\6O2Q6) + Q Qen j

V / Q.

2g ieozc, (для ламинарного потока).

щЬ) \ бОЬгСЧ J

(79)

[бОгСщЬ

0.16 6062

I Qa \ 1щ Г? Ьг-

(80)

(для турбулентного потока). *

Составляющая потерь Дрв определяется из уравнения

где ~-= Где - радиус всасывающего отверстия.

* По данным ВИГМ для потока в узкой щели 5 Рыбкин и Усов 88

Составляющей потерь Др, представляющей собой инерционные потери на длине междузубовой впадины, по малости ее величины можно в дальнейших расчетах пренебречь.

Суммируя составляющие потерь на всасывании, обозначая при этом значения, имеющие множители и nv, в формуле для определения потерь при ламинарном потоке соответственно через К

и Kj, а значения, имеющие множители и gyv в формуле для

V п

определения потерь при турбулентном потоке соответственно через Kg и К4, получим следующие зависимости бескавитационной работы: для ламинарного потока .у.

Pec~Pi

для турбулентного потока

... Pec - Pt>

где

(81)

-У

60-Kdi

ч

(83)

Кз = Ki,

0.1630fcl / \2 /и, Qe-4 ..

Практика показывает, что надежность и, в значительной степени, бесшумность работы насосов требуют, чтобы разность между значениями левой части и правой неравенств (81) и (82) составляла не меньше 0,35 = 0,4 кГ/см.

Зависимости (81) и (82) характеризуют влияние конструктивных и эксплуатационных параметров на величину потерь напора во всасывающей камере насоса. Можно заметить, что при заданном режиме работы и свойствах нагнетаемой жидкости всасывающая способность насоса возрастает с уменьшением коэффициентов Ki, Кг и К4. Значения этих коэффициентов определяются главным образом диаметральными размерами и величиной междузубового зазора. Увеличение размера междузубовой щели улучшает условия подвода жидкости в междузубовое пространство, снижает влияние вязкости и увеличивает допустимое для заданных условий число оборотов приводного вала.

При применении установленных выше зависимостей потерь на всасывание некоторые трудности вызывает определение значений и - величин переменных и являющихся функциями угла поворота роторов.

в первом приближении, обеспечивающем определенный запас надежности, можно допустить средне-приведенный размер междузубовой щели, равным боковому зазору в зацеплении {С^ = С„), а средне-приведенную длину щели считать равной двойной высоте головки зуба (/ = 2h = 2т). Имея в виду вероятность турбули-зации потока при заполнении жидкостью междузубового пространства применим для этого случая в качестве основной формулу (82) и представим ее в более удобной для анализа форме, полагая условно,

что я (i?2 - /?2) = -f .

После промежуточных преобразований зависимость (82) приобретает следующий вид:

(84)

В этой зависимости значение в квадратных скобках безразмерное и характеризует соотношение размеров рабочих органов насоса. Значение в круглых скобках последнего члена суммы также безразмерное и характеризует влияние вязкости жидкости и числа оборотов роторов.

Значение в квадратных скобках формулы (84) может служить критерием при оценке всасывающей способности шестеренных насосов, работающих на жидкостях одинаковой вязкости и одном и том же числе оборотов.

Обозначим множитель правой части зависимости (84), заключенный в квадратные скобки, через К^с- Тогда

\.. Рвс - Р1>КесУ V,

откуда r--.f:--

k.,<v().-(85)

Анализируя зависимость абсолютного давления на входе в насос (84), можно заметить, что величина первого члена суммы заключенного в квадратные скобки, менее значима, чем величина остальных членов, а выражение, заключенное в круглые скобки, последнего члена суммы по мере уменьшения вязкости нагнетаемой жидкости приближается к единице.

Наибольшее влияние на величину выражения, заключенного в квадратные скобки, оказывают геометрические параметры b (/?2 - Rj), и z. Это является основанием для вывода, что при заданном абсолютном давлении на входе во всасывающую камеру насоса и заданной производительности бескавитационная работа возможна только при определенных размерах рабочих органов. 5* .... . 67

Кроме того, зависимость (84) позволяет определить возможности работы при большем разрежении или большей вязкости жидкости. В последнем случае требуется увеличение ширины роторов Ь, размеров входного отверстия й^ проходного сечения между профилями зубьев С и активной высоты зубьев, определяемой разностью

Так как изменение перечисленных величин может варьироваться лишь в определенных пределах, то в случае, когда от насоса требуется высокая производительность Qe(i) целесообразно уменьшить высоту всасывания Н^.

Для насосов определенного типоразмера можно считать, что абсолютное давление во всасывающей камере изменяется пропорционально квадрату скорости вращения приводного вала.

Бескавитационная работа насоса может быть нарушена нагнетанием жидкости, содержащей растворенные и увлеченные газы и воздух.

В начале этого раздела выяснено, что потери на всасывании связаны с характером и степенью заполнения междузубовых впадин роторов.

Факторами, определяющими надежность и эффективность заполнения междузубовых впадин, как известно, являются:

1) давление на входе во всасывающую камеру; 1

2) скорость вращения роторов,

3) вязкость жидкости и ее упругость; *

4) продолжительность нахождения рабочих зубьев в зоне всасывания;

5) количество присутствующего в нагнетаемой жидкости воздуха или газа; ,

6) размер вредного пространства. Ранее установлена взаимосвязь с основными геометрическими

параметрами рабочих органов насоса первых трех факторов и определены возможные составляющие внутренних потерь на всасывании.

Изучение влияния на производительность насоса остальных факторов также является необходимым. Известно, что недозаполнение рабочих камер насоса ведет к снижению его производительности и ухудшению коэффициента полезного действия. Кроме того, недозаполнение междузубовых впадин вызывает эрозию деталей насоса в результате резкой пульсации давлений в камере нагнетания, в момент, когда в нее входит недозаполненная междузубовая впадина. От ударов жидкости на стенках корпуса возникают микроскопические трещины, которые и являются начальными очагами эрозионного разрушения.

При больших скоростях вращения роторов, кроме перечисленных ранее геометрических факторов, на условия бескавитационной работы насосов влияет недостаточность времени нахождения междузубовой впадины в зоне всасывания, в результате чего каждая рабочая пара зубьев роторов уходит из камеры всасывания с недозаполненным междузубовым пространством. 68

Для приближенных расчетов длины дуги камеры всасывания, при которой обеспечивается надежное заполнение междузубовой впадины (при определенных условиях разрежения) [14], можно применять предлагаемую ниже методику.

Обозначим через 5 длину дуги камеры всасывания, через - время, потребное для прохождения жидкостью всей глубины впадины (/ = 2т) и через /г - время пребывания междузубовой впадины в зоне всасывания на дуге длиной 5. Условие надежности заполнения междузубовых впадин требует соблюдения следующего неравенства:

t->t,. (86)

Тогда при вращении роторов со скоростью п об/мин. , 30S 20S

Средняя скорость движения жидкости при заполнении междузубовой впадины может быть определена из уравнения

где ф - коэффициент скорости, равный ~0,5;

Арлз - разность между значениями давлений на входе в камеру всасывания и в наиболее удаленной точке междузубовой впадины.

При пренебрежении влиянием вязкости жидкосги Арз определяется из уравнения

Ар, = р -p-fKi/i

Считая скорость движения и^ постоянной {и^ = const), можно определить время ty, необходимое для прохождения жидкостью на всю глубину впадины, по следующему уравнению.

/ 2т - ,

Тогда неравенство (86) принимает вид

20S 2т V

tiDe

УРмз 2g

4. ВЛИЯНИЕ НА ВЕЛИЧИНУ ПОТЕРЬ РАСТВОРЕННОГО И УВЛЕЧЕННОГО ЖИДКОСТЬЮ ВОЗДУХА

Работами различных исследователей [3], [14], [16], [19] обнаружено существенное влияние на производительность насосов присутствующей в нагнетаемой жидкости газовой составляющей, которая ухудшает условия заполнения рабочих камер. Это объясняется тем, что часть объема рабочих камер занимается примешанными к жидкости и расширившимися воздушными пузырями и газом (выделившимся из раствора).

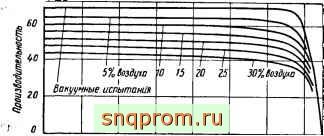
На фиг. 31 изображены кривые, характеризующие работу насоса на жидкостях с различным содержанием воздуха.

750 650

550 <>50 350 250 150 ммрт.т Даблеиие но Входе

...

Фиг. 31.

Присутствие воздуха является причиной серьезного ухудшения характеристики всасывания из-за наличия защемленного пространства, откуда определенный объем жидкости п:!реносится обратно в камеру всасывания. Здесь возвращенный с жидкостью воздух вновь расширяется и, занимая часть объема, увеличивает степень недо-заполнения междузубовых впадин.

С увеличением вакуума на входе в насос увеличивается объемное содержание газовой составляющей и уменьшается количество масла, что приводит к падению объемного коэффициента полезного действия насоса.

Количественное содержание растворенного воздуха в жидкости определяется коэффициентом абсорбции а, характеризующим относительный объем растворенного в жидкости воздуха. Коэффициент абсорбции представляет собой функцию физических свойств жидкости (ее способности растворять под атмосферным давлением воздух) и при неизменной температуре, как это следует из закона Генри, является постоянной величиной.

Экспериментально установлено, что в условиях нормальной (20° С) температуры и атмосферного давления содержание растворенного воздуха в минеральных маслах достигает 8-10%.

В отличие от коэффициента абсорбции а, коэффициент р характеризует относительный объем содержащегося в масле перемешанного (нерастворенного) воздуха. Этот коэффициент в очень малой

1 ... 3 4 5 [ 6 ] 7 8 9 ... 18