Главная страница сайта  Российские промышленные издания (узловые агрегаты) 

1 2 3 [ 4 ] 5 6 7 ... 18

рой зуб ротора не имеют полного контактирования с сопряженными зубьями по всей ширине от переднего до заднего торца

В условиях плотного беззазорного зацепления зубьев роторов постоянная изоляция камер нагнетания и всасывания возможна и при больших, чем в зацеплении с боковым зазором, значениях угла наклона зубьев р^. Значения угла при беззазорном зацеплении определены условием

Маб<2(е,-4) (39)

и

tgPa<2-ra(.-4)- (40)

В пределах обусловленных величин угла Р^ достигается непрерывное разделение камер нагнетания и всасывания контактными линиями между рабочими (по линии АВ) и нерабочими (по линии CD) сторонами профилей зубьев зацепляющихся роторов (фиг. 15, б). К моменту окончания контактирования рабочих профилей зуба 2 в точке В на задней торцовой плоскости, на передней торцовой плоскости вступает в контакт в точке D с зубом ведомой шестерни последняя точка нерабочей стороны этого зуба. При дальнейшем вращении к моменту выхода из зацепления нерабочей стороны зуба 2 (в точке С на задней торцовой плоскости) в точке А переднего торца зуб 1 ведущего ротора контактирует с соответствующим зубом ведомого ротора уже по всей ширине и т. д. При значениях угла Р^, больших нежели обусловлено неравенством (40), постоянная изоляция камер всасывания и нагнетания отсутствует и при беззазорном зацеплении (фиг. 15, е).

Для определения скорости объемной подачи (амплитудной производительности) двухроторных шестеренных насосов с косозубым зацеплением при углах р^, не превышающих установленных зависимостями (38) и (40) величин, рассмотрим участок пары зацепляющихся косозубых роторов, ограниченный двумя плоскостями, перпендикулярными к осям роторов и находящийся на расстоянии у и {y+dy) от переднего торца роторов.

Зацепление косозубых роторов элементарной ширины dy можно рассматривать как прямозубое (плоскостное) и считать для него справедливыми все зависимости, полученные для прямозубого зацепления.

Для косозубой шестерни элементарной длины dy формула для скорости объемной подачи (15) запишется в следующем виде:

dq.oc = [tg а,+- tg а, ~ (tg а, - cp/]dy. (41)

Здесь сру = ср + у представляет собой величину текущего

угла поворота ведущего ротора, соответствующего точке контакта профилей в сечении, расположенном на расстоянии у от переднего торца, ф - некоторое (принятое за наименьшее) значение угла поворота ведущего ротора, отнесенное к передней торцовой плоскости, tg - тангенс угла зацепления в торцовом сечении.

Подставляя в формулу (41), значение ф^, и интегрируя в пределах от у = О до у = 6 получим формулу для определения скорости объемной подачи шестеренных насосов с косозубыми роторами

Я.ос = rlb [it а, - tg а, - (tg а, - ср) -f

+ 4tga, ,) lM..]. (42)

Эта формула справедлива, как для зацепления с боковым зазором, так и для беззазорного зацепления (подача производится рабочими сторонами зубьев). Максимальных значений функция (42) достигает, когда

tgPd b

(р== tga,-

гд 2

>

Следовательно,

Якос(наи6) = МГдб

(43)

Наименьшее значение д^с рассматриваемом интервале угла поворота ведущей шестерни) имеет, когда

При этом скорость объемной подачи определяется по формуле 9 ..( .л,) = <Ь(Va.-tg==a.-e--iVV (44)

Из сравнения формул (43) и (44) с аналогичными формулами для прямозубого зацепления (16) и (17) следует, что наибольшие и наименьшие значения скорости объемной подачи у насосов с косозубыми роторами меньше, чем значения скорости у насосов с прямозубыми роторами. Амплитуда колебаний первой гармоники, равная разности между наибольшими и наименьшими значениями скорости объемной подачи, у прямозубых и косозубых роторов, определяется величинами

Идентичность этих величин свидетельствует о том, что использование роторов с винтовыми зубьями (при условии сохранения постоянной изоляции между камерами нагнетания и всасывания), не уменьшает величину пульсации подачи жидкости. Справедливость этого вывода подтверждается данными осциллографирова-ния (фиг. 16) пульсации давления в нагнетательном трубопроводе шестеренных насосов с винтовыми и прямыми зубьями.

Формулы для расчета геометрической производительности насоса с косозубым зацеплением за один оборот ведущего ротора найдутся 42 - U

последовательным двойным интегрированием уравнения (41), в котором след зазором

ром следует принять, что < - - Тогда для зацепления с боковым

Фиг. 16.

а) г = 8; р, = 9°

(45)

а) Z = 8; = 9° 1

б) 2 = 12; р^ = 0° I = *50 об/мин.

Для беззазорного зацепления

Яг (.) .ос. бз = 2z \ f (tg а, - tg а, -

- tg а, (<р + у) j di/dcp. (46)

Интегрируя значения (45) и (46) при зацеплении с боковым зазором в пределах от Ф1 = tg - до фг = tg -f (2 - е),

а при беззазорном зацеплении в пределах от фд = tg -

до == tg --- {е - I) и имея в виду, что для зацепления

с боковым зазором Slh = 2- (е - I), а для беззазорного заце-

пления 6 = 2 у - получим следующие формулы для расчета геометрической производительности шестеренных насосов с косозубыми роторами: для зацепления с боковым зазором

для беззазорного зацепление

Q.,i) o. =27cbr2[tga,-tga,-(e-e4-J-)

(47)

(48)

При значениях угла наклона зубьев больших, чем обусловлено неравенствами (37) и (38), непрерывная изоляция полостей нагнетания и всасывания отсутствует. Для этого случая, невозможно

поэтому, установить точную аналитическую зависимость для определения объема нагнетаемой жидкости.

Степень неравномерности подачи жидкости

В гидравлических приводах метал-ops] I I лорежущих станков шестеренные насосы широко используются для сообщения возвратно-поступательного движе-o,aii\ -\ г \-I ния столам (или шлифовальным бабкам) плоско-, кругло- и внутришли-

0 I I I [ ) фовальных станков, на которых произ-

Ю п Г8 2Z г водятся отделочные операции. Нерав-Чисглзубьеб номерность подачи жидкости является

Фиг. 17. ОДНОЙ из главных причин неравномер-

ности перемещения подвижных узлов станка и отрицательно влияет на качество и точность размеров шлифуемых поверхностей деталей. Учет степени неравномерности подачи в случаях использования шестеренных гидронасосов в шлифовальных станках может оказаться необходимым при расчетах на вибрацию системы станок-инструмент-деталь .

Мерой пульсации потока жидкости является степень неравномерности, которая оценивается посредством следующих коэффициентов:

9рез (наиб) Ярез (наим)

Яр. (наиф)

(49)

- рез (наиб) рез {наим\

Ярез (наиб) ~ рез (наим)

(SO)

Для сравнения на фиг. 17 изображены кривые изменения неравномерности подачи в зависимости от числа зубьев для случаев с боковым зазором в зацеплении и с беззазорным зацеплением при наиболее рациональной системе канализации защемленной жидкости в сторону нагнетания.

Экспериментальное определение геометрической производительности

Для подтверждения справедливости найденных в предыдущих разделах аналитических выражений геометрической производитель-

5 < 7

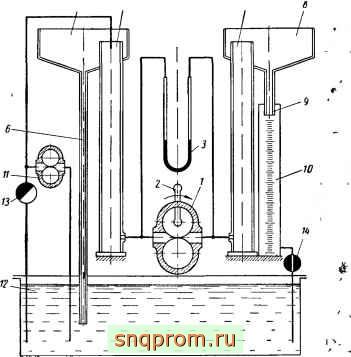
Фиг. 18. Схема установки (стенда), применяемой для про- . верки геометрической производительности шестеренных насосов.

ности была произведена их эксперилентальная проверка на специально сконструированной для этой цели испытательной установке (фиг. 18).

Возможность утечек жидкости из одной камеры насоса в другую устраняется путем создания на сторонах всасывания и нагнетания

рйЁнЫх статических напоров. Контроль paBeHctfea статИЧесКиХ напоров производится с помощью дифференциального водяного манометра 3. При медленном вращении рукоятки 2, исключающем возникновение кавитации, жидкость, заполняющая рабочие камеры насоса, переливается через верхний край трубы 7 и стекает через воронку 8 и трубку 9 в мерный бачок 10. Для обобщения выводов по результатам испытаний в качестве объектов были взяты шестеренные насосы различных производительностей с различными числами зубьев и с различными геометрическими параметрами, характеристики которых помещены в табл. I.

Таблица 1

Типы насосов (марка, фирма)	Параметры роторов
	Число зубьев ротора	Модуль в мм	Коэффициент коррекции	Наружный диаметр в мм	Межцентровое расстояние роторов в мм	Ширина роторов в мм
Ш-25......
Ш-35......
Ш-50......
нш-г5.....		4 5		57,6	48,6
ЕКМ , модель
РНР-0,4 ....			0,33
То же, модель
РНР-6,3 ....
.Keelavite модель
G-105 .....		2,54	0,14	64,21	59,13	26,988
То же, модель
2004 ......		4,233		50,8	42,330	17,463
Опытный МГ-11-11

Результаты проведенных испытаний (табл. 2) свидетельствуют о достаточно близком совпадении расчетных и опытных данных. Для насосов с шестернями, изготовленными в пределах посадок X или Л по наружному диаметру и в пределах посадки Д по ширине с колебаниями межцентрового расстояния А^, не превышающими +0,03 мм. (пределы величин отклонений от нормальных размеров деталей при серийном производстве их) значения расхода, полученные опытным путем, составляют 97-98% от расчетных. Наибольшие отклонения от расчетных значений геометрического расхода имеют место у насоса НШ-35 (около 10%). В результате замеров, произведенных после разборки этого насоса, обнаружены значительные отклонения действительных размеров деталей от принятых при расчете.

Кроме этого, возможными причинами расхождения расчетных и опытных значений геометрической производительности насосов могут быть:

а) большие зазоры между торцами роторов и опорными втулками, через которые может быть вытеснена защемленная жидкость;

Типы насосов (марка, фирма)

Средние показания мерного бака на 100 оборотов рукоятки в см

Опытное значение геометрической производительности за один оборот в см

Расчетное значение геометрической производительности за один оборот по действительным размерам деталей за один оборот в см

Таблица S

По теоретическим размерам деталей за один оборот в см

Ш-25 . .

Ш-50. . НШ-35

ный) . МГ-11-11 ,ЕКМ , модель

РНР 0,4 ЕКМ ,- модель

РНР 6,3 Keelavite , мо

дель G-105 nKeelavite ,

дель 2004 . . Опытный МП 1-11*

2204,0 4150,0

3702,0 689,5

470,0

7438,0

2465,0

1951,0 667,0

22,040 41,500

37,000 6,895

4,70

74,38

24.650

19,51 6,670

22,174 41,825

37,395 6,947

4,74

74,926

24,944

19,752 6,372

22,518 42,701

41,260 7,192

4,950

77,651

25,682

20,197

6,969

* При направлении канализации защемленной жидкости в сторону всасывания. (Данные всех остальных замеров относятся к случаю канализации защемленной жидкости в сторону нагнетания.)

б) неточное относительное расположение разгрузочных канавок, в результате чего камеры нагнетания и всасывания могут сообщаться через пространство защемления, а защемленный объем вытесняться одновременно в сторону нагнетания и в сторону всасывания;

в) отклонения от эвольвентного профиля боковых поверхностей зубьев, вызывающие неплотное прилегание и выдавливание защемленного объема через зазоры в зацеплении;

г) эксцентричность расположения роторов на валах и шеек опорных валов в подшипниках, ведущая к колебаниям значений Л„; .

д) относительное скольжение профилей зубьев.

Влиянием названных выше причин можно объяснить имеющиеся расхождения в значениях геометрической производительности, полученных опытным путем и в результате расчетов по действительным размерам деталей.

Различие этих значений, как следует из данных табл. 2, является незначительным.

Основываясь на экспериментальных данных, действительные Значения геометрической производительности насосов, определяемые размерами рабочих органов и принятым способом канализации, при погрешностях изготовления, находящихся в пределах допустимых отклонений, могут оцениваться расчетными данными. Полученными по предложенным выше формулам, с коэффициентом 0,97-0,98.

i. tE0PETH4ECKHE ЗНАЧЕНИЯ КРУТЯЩЕГО MOMEHtA И МОЩНОСТИ НАСОСОВ

Крутящий момент ,. >

Формулы для теоретических значений крутящего момента можно получить из уравнения работы, производимой при повороте роторов насоса на элементарный угол

AprfQ = Mdcf, ,

откуда M = -p. - j

Имея в виду, что ф = adt, получим следующую формулу:

=ТЖгДР = 9ДР1сГсл<. . (51)

Здесь = q - скорость объемной подачи (амплитудная производительность) в мм/сек; Др - перепад давлений в камерах нагнетания и всасывания в кГ/см.

Подставляя в формулу (51) известные нам значения амплитудной производительности, найдем соответствующие значения крутящего момента: момент, действующий на ведомую шестерню,

= %аДр 77 =-- 21г![(tg . -(2tga, cp)]b, (52)

момент, действующий на ведущую шестерню,

ещ = Яещ^р4=.гЖ-. = -Ь, / (53)

суммарный крутящий момент на приводном валу ,

- (tga - mf]bKrcM. (54)

Наибольших значений крутящий момент достигает, когда Ф = tg а^. Следовательно,

Мреэ = (tg2 а, - tg а,) b кГсм. - (55)

Среднее значение суммарного теоретического крутящего момента соответствует рассмотренному ранее среднему значению геометрической (теоретической) производительности насоса за один оборот ведущего ротора.

I Q ,[> Др

В соответствии с формулой М^ - -- получим: для прямозубого зацепления с боковым зазором

М

ср (т) = (tg а, - tg - 1 Ь кГсж, (56)

к

Для прямозубого беззазорного зацеплений

in.) = (tg а, - tg а, - 6 кГсм; (5?)

для насосов с косыми зубьями роторов Мер (гп) =-frl [tg ffi tg а, -g- {в^ -2в + 2)] b кГсм. (58)

Мощность

Формула для мгновенной (амплитудной) мощности может быть получена подстановкой в уравнение N - М^ и значения М^ из формулы (54).

Тогда

Npe. = г1 Itg а, - tg а, - (tg а, - ср)] b л. с. (59)

Среднее значение теоретической мощности определяется из известного соотношения N = 2кпМср, в которое должны быть подставлены соответствующие значения М^ согласно характеру зацепления. Имея в виду, что все линейные размеры даны в миллиметрах, давление в кГ/см и п число оборотов в минуту, средние значения теоретической мощности, выраженные в лошадиных силах определяются следующими зависимостями:

для прямозубого зацепления с боковым зазором

Nop <m) = Ар 1 (tg а, - tg а„ -1. ) Л. с; (60)

для прямозубого беззазорного зацепления -

iVcp(m) = Ар ,tg2 а, -tga - -f )л.с; (61)

для насосов с косыми зубьями роторов

- Ар [.g. - tg с - 2 + 2)] - с. (62)

Средние значения теоретической мощности и крутящих моментов для прямозубого зацепления соответствуют случаям работы насосов с использованием избыточного объема. Для предварительных расчетов часто употребляемые зависимости М^ и Np могут быть упрощены, если пренебречь величиной слагаемого, перед которым стоит

, и влиянием коррекции зацепления. Тогда Ncp ( ) = А р {г+1)л.с, (63)

Mcpim) = p-(z+1)кГсм. (64)

4 Рыбкин в Усов 88

ГЛАВА II /..;,.v

ТЕОРЕТИЧЕСКИЕ ЗНАЧЕНИЯ ВНУТРЕННИХ ПОТЕРЬ

В ШЕСТЕРЕННЫХ НАСОСАХ ,

\ V 1. ОБЪЕМНЫЕ ПОТЕРИ (УТЕЧКИ)

В правильно сконструированном насосе и при отсутствии кавитации объемные потери определяются исключительно величиной зазоров между сопряженными поверхностями рабочих органов и уплотняющих деталей.

Утечки жидкости из камеры нагнетания в камеру всасывания могут иметь место по трем основным каналам:

1) через радиальный зазор между цилиндрическими поверхностями шестерен и расточек в корпусе;

2) через зазор между торцовыми поверхностями шестерен и поверхностями уплотняющих деталей;

3) через зону зацепления вследствие погрешностей между зубового контактирования.

Все расчетные зависимости для вычисления объема утечек нами определяются на основании доказанного Н. Н. Петровым положения о ламинарном характере движения жидкости в узких щелях и положения установленного Б. В. Дерягиным, о неизменности свойств жидкости в зазорах, больших 0,1 мк.

Утечки через радиальные зазоры

Данное W. Е. WilsonoM [491 применительно к радиальным зазорам роторных насосов частное решение уравнения Рейнольдса позволяет определить величину расхода через дугообразную гладкую щель между вращающимися ротором и корпусом насоса .

В окончательном виде зависимость, полученная для условий установившегося движения жидкости в щели, представляется формулой . ,

где / - длина Дуги, образующей радиальную щель (фиг. 19). Для

Подробный вывод этой расчетной формулы изложен в книге Т. М. Башта [3].

1 2 3 [ 4 ] 5 6 7 ... 18